磁流變阻尼器的改進多項式模型及驗證

周鐵明， 陳恩偉， 陸益民， 劉正士, 陳無畏

(合肥工業大學 機械與汽車工程學院，合肥 230009)

磁流變阻尼器(Magnetorheological Damper, MRD)以其結構簡單，阻尼力連續可調，響應快，出力大，可靠性高且能耗低等優良性能，成為新一代高效的半主動控制的實現載體，廣泛應用車輛(含汽車、高速列車)、衛星隔振平臺、大型斜拉橋等的半主動振動控制[1-4]。為了設計控制策略和評價MRD在振動控制中應用的可行性，需要建立MRD的力學模型。由于MRD存在著一種特殊的力學性能-滯回特性，使其力學模型十分復雜，給建立精確的阻尼力模型和參數識別帶來困難。

應用流變學理論分析流變后的MRD的力學特性非常復雜和困難，因此，通常采用MRD力學性能試驗的結果來建立其數學模型?；诖帕髯円呵昂颓蠖际撬苄郧仪暗淖枘徇h大于屈服后的阻尼的假設，Stanway[5]提出了非線性雙粘性模型。該模型可較好地擬合阻尼力-位移滯回特性和阻尼器在每個振動周期內的能量耗散情況，但不能精確地擬合屈服前的阻尼力-速度滯回特性。Li等[6]對非線性雙粘性模型進行拓展，提出了非線性滯回雙粘性模型。該模型可以更好地模擬屈服前的阻尼器滯回特性，但不能擬合試驗中MRD在低速時的回復力衰減現象。Spencer等[7-8]提出了Bouc-Wen模型，該模型數字上易于處理，能較好地反映阻尼器在低速時的滯回情況，但模型復雜，參數較多，不易辨識。Choi等[9]用多項式擬合阻尼力-速度曲線，令阻尼力為以活塞速度為自變量的一元高次多項式，強行使多項式系數與激勵電流為線性關系。

本文在MRD力學性能試驗的基礎上，提出改進的多項式模型-分段3次多項式模型。該模型將阻尼力-速度曲線分為正加速度曲線(右支)和負加速度曲線(左支)，采用文獻[6]的分段方法將每支曲線分成3段，每段曲線用多項式進行擬合，且每個多項式的系數與激勵電流不再為線性關系。

1 磁流變阻尼器的力學性能試驗

圖1 磁流變阻尼器力學性能試驗曲線

2 磁流變阻尼器建模

選擇激勵幅值為15 mm，頻率為1 Hz，控制電流強度為0 A、0.5 A、1 A、1.5 A、2 A、2.5 A和3 A工況下的試驗數據，采用基函數為多項式的最小二乘法進行MRD的動力學模型建立及參數識別研究。

2.1 多項式模型

文獻[9]認為6次或更高次多項式就可以完全反映阻尼力-速度曲線的滯回特性，但彼此區別不大。在實際應用過程中發現，6次多項式和9次多項式的擬合精度差別較大，9次多項式的擬合精度比6次高；但9仍沒達到精度要求。雖然多項式的階數越高，擬合效果越好，但這也將使得需要辨識的參數變得更多。經過測試，12次的擬合效果很好，已經滿足精度要求。12次多項式模型的計算公式為：

(1)

ai=bi+ciIi=0,1,…,12

(2)

激勵幅值15 mm、激勵頻率1 Hz、控制電流1 A工況下9次，12次多項式擬合效果如圖2所示。

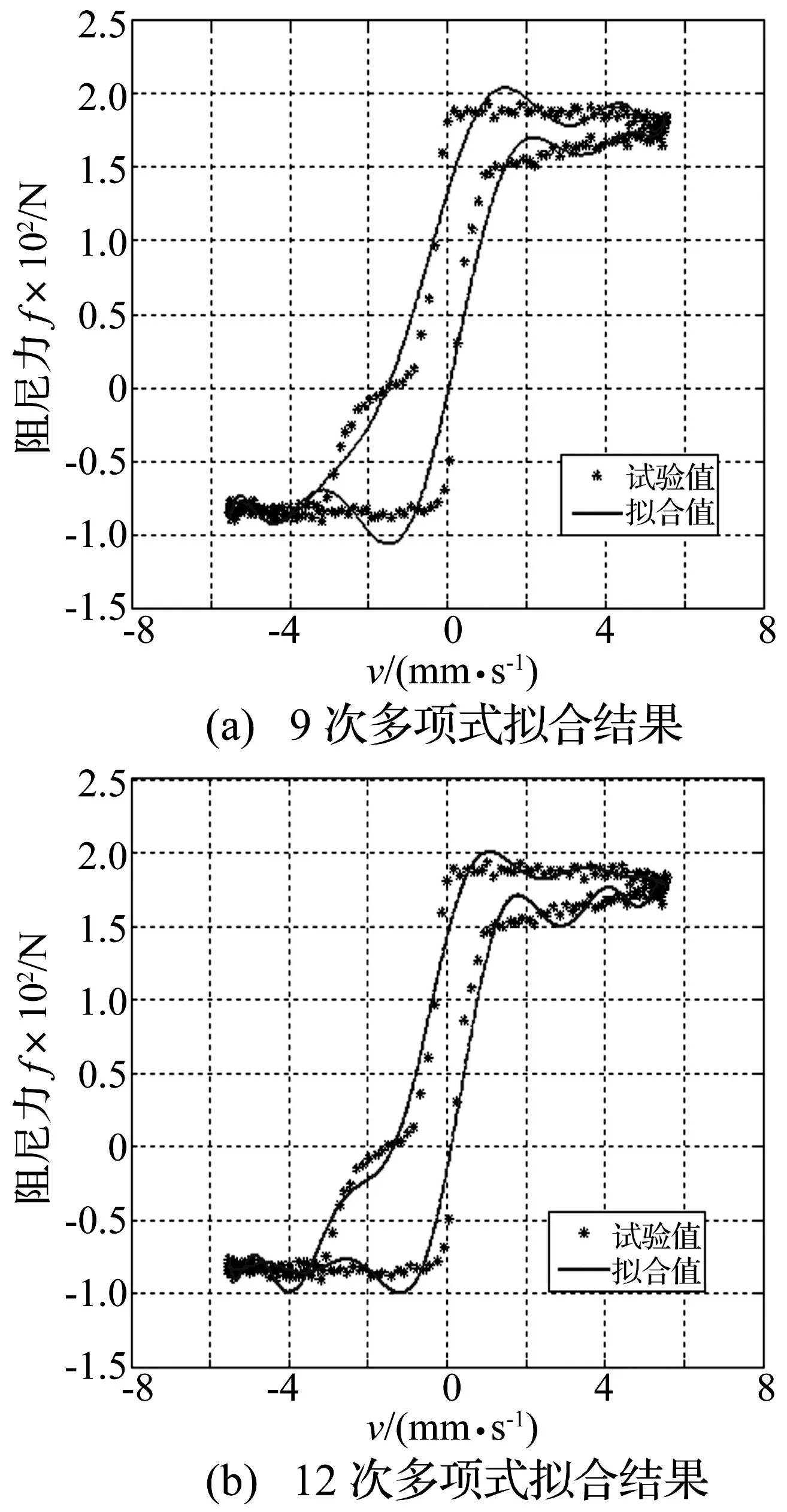
圖2 各階多項式擬合效果對比圖

雖然12次多項式在高速區的擬合效果與實測結果有些偏差，但誤差仍在可接受范圍之內，因此采用12次多項式進行擬合。用最小二乘法[11]可以很容易地辨識出各電流情況下的ai，如式(3)所示。

(3)

式中，ai為待辨識多項式系數；m為參與辨識的實測數據點數，m=12；vj為參與辨識的MRD活塞速度值；Fdj(vj)為參與辨識的實測阻尼力值，與vj一一對應；Fd(vj)為vj對應的12次多項式模型計算阻尼力值。

12次多項式強行使ai與電流I為線性關系，所以能夠用直線擬合法辨識出截距bi和斜率ci值。當速度的絕對值較大時，多項式曲線的兩端出現了劇烈的振蕩，這就是龍格現象(Runge’s Phenomenon)，如圖3所示。造成這種現象的原因有:

(1) 速度絕對值較大處，采樣點較多，相鄰兩個采樣點之間，該多項式不一定能很好地逼近理想函數，產生很大的誤差。

(2) 高次多項式由于計算量大，舍入誤差的不斷積累，使得多項式兩端發散，造成擬合結果不合理。

(a) 15mm、1Hz、0A時 (b) 15mm、1Hz、1A時 (c) 15mm、1Hz、3A時

2.2 分段3次多項式模型

Runge現象的出現，證明了高次多項式擬合具有較大的風險，因此在使用多項式模型時應盡量降低多項式的次數。為了解決Runge現象，可采用分段低次多項式對曲線進行擬合。借鑒文獻[6]提出的非線性滯回雙粘性模型的分段思想，預先確定的4個屈服速度，將正、負加速度曲線各分成3段，以屈服前后的速度點作為分段點，對每段曲線用多項式進行擬合，如式(4)所示。研究發現，雖然需要預先確定4個屈服速度，增加難度，但是計算所需多項式次數大大降低，能較好地克服了Runge現象：原來一整支曲線需用12次多項式擬合才能獲得不錯的效果，現在每段曲線只需用3次多項式擬合即可，而且擬合精度也得到提高。擬合結果如圖4所示。

(4)

式中，ad1、ad2、ad3、au1、au2、au3為各分段多項式系數；

v1、v3為實際阻尼力-速度曲線減速時的屈服速度，為該分支曲線兩個轉折處的速度值；v2、v4為正加速時的屈服速度，也是該分支曲線兩個轉折處的速度值。v1、v2、v3、v4均是電流I的函數；

圖4 分段3次多項式模型擬合效果

對比圖2和圖4，分段3次多項式的擬合精度比12次多項式的擬合精度高。為防止分段3次多項式模型的進一步復雜化，各分段多項式系數與電流之間用線性關系擬合，即a=b+cI。

分段多項式模型雖然提高了擬合精度并且能夠防止Runge現象出現，但也存在一個明顯的問題，即分段模型不是光滑連續，在每兩段曲線的連接處可能出現不連續現象。為了使連接處盡量光滑過渡，在對每個分段計算時，分別向前和向后多取0.1N(N為該段點數)個采樣點，最后該段共有1.2N個采樣點參加計算。這樣可以避免各分段的連接處出現不連續[11]。

采用最小二乘法對分段3次多項式模型進行參數辨識，結果如表1所示。

表中參數依據規則“下標d表示右支曲線，u表示左支曲線；下標中第1個數值1、2、3分別表示第1、2、3段曲線；下標中第2個數值0、1、2、3分別表示多項式的

常數項、一次項、二次項、三次項系數的擬合值”類推。如“，bd10、cd10表示右支曲線第一段多項式中常數項ad10的擬合參數值，即ad10=bd10+cd10I”。

屈服速度v1、v2、v3、v4與電流的關系如圖5所示。

圖5 屈服速度與電流I的關系

表1 分段3次多項式模型參數表

經過多項式擬合，得到各屈服速度與電流的關系，如式(5)～式(8)所示。不同型號的磁流變阻尼器的結構、尺寸以及內部線圈的扎數不盡相同，所以4個屈服速度與電流的關系是針對一定型號磁流變阻尼器而確定的系數。磁流變阻尼器的型號改變，系數也會隨之改變。

v1=-0.007 248I3+0.141 633I2-0.136 455I+1.059 053

(5)

v2=0.057 119I4-0.410 437I3+1.030 562I2-1.044 846I+0.339 158

(6)

v3=0.043 268I3-0.153 423I2+0.053 011I-0.069 076

(7)

v4=-0.207 829I3+1.417 490I2-3.524 325I-0.888 611

(8)

3 模型驗證及誤差分析

3.1 模型驗證

利用參數辨識結果，計算未參與模型辨識的3種工況下模型的預測阻尼力，并與實測阻尼力值進行比較，結果如圖6所示。

從圖中可看出，分段3次多項式模型的計算阻尼力和實測阻尼力值基本重合，Runge現象消失，說明該模型能夠較好地描述MRD的阻尼力-速度之間的非線性特性和滯回特性。

3.2 誤差分析

由于平均誤差是對每一段上不同點的平均，并不能反映每一點的情況，按照誤差分析常用的相對誤差分析方法，本小節通過分析在幅值為15 mm，頻率為1 Hz激勵下，各對應速度下模型計算阻尼力值與實測阻尼力之間的相對誤差，進一步評價分段3次多項式模型的有效性。

模型的相對誤差由式(9)表示：

(9)

式中，Fd(vj)表示vj速度下分段3次多項式模型的計算阻尼力值；

Fdj(vj)表示vj速度下實測阻尼力值。

選取0.5 A、1.5 A、2.5 A電流下的數據進行誤差分析，分別代表小電流、中電流、大電流三種情況，計算結果如圖7所示。

(a) 15mm、1Hz、0.5A時 (b) 15mm、1Hz、1.5A時 (c) 15mm、1Hz、2A時

(a) 15mm、1Hz、0.5A時 (b) 15mm、1Hz、1.5A時 (c) 15mm、1Hz、2.5A時

eu1、eu2、eu3分別表示左支曲線第1段、第2段、第3段的模型計算阻尼力值與實測值的相對誤差。從圖7可看出，3種電流情況下，分段3次多項式模型均是第1段和第3段時誤差較小，第2段時誤差最大，也即模型在滯環速度區(低速區)的誤差最大；即使同在第2段，左支曲線的誤差比右支曲線的誤差大得多。這是因為在第2段的采樣點數少于第1段和第3段，造成第2段多項式的擬合誤差大于第1段和第3段，經過參數辨識，誤差積累放大，再利用模型計算阻尼力時，第2段的誤差自然比第1段和第3段大。由于模型計算出的穿越速度滯后于實際的穿越速度，導致在計算穿越速度與實際穿越速度之間，模型的計算阻尼力值與實測值符號相反，式(9)中的分子非但沒有減小，反而增大，變得比分母還大，最終的誤差計算值超過了100%，這就是第2段上支曲線的最大誤差分別為110.6%、369.1%、397.8%的原因。雖然誤差超過了100%，但在穿越速度附近，阻尼力的值比較小，這么大誤差產生的實際影響并不大。

隨著電流的增大，第1段和第3段及右支曲線第2段的誤差逐漸減小，驗證了多項式系數對于電流影響的敏感性。從整體來看，分段3次多項式模型具有較高的精度，能夠較準確地反映MRD的阻尼力-速度關系。

4 結 論

(1) 6次多項式或更高次多項式都可以反映阻尼力-速度曲線的滯回特性，但區別較大。多項式的階數越高，阻尼力-速度曲線的擬合效果越好，但高次多項式擬合易出現Runge現象，導致擬合曲線的兩端出現劇烈地振蕩。

(2) 經過驗證，分段3次多項式模型能夠有效地消除Runge現象，且擬合精度較高。因此，分段3次多項式模型能夠較好地描述MRD阻尼力-速度曲線的非線性特性和滯回特性。

參 考 文 獻

[1]劉永強, 楊紹普, 申永軍.基于磁流變阻尼器的汽車懸架半主動相對控制[J].振動與沖擊, 2008, 27(2):154-156.

LIU Rong-qiang, YANG Shao-pu, SHENYong-jun. Semi-active relative control schemes forvehicle suspension using amagnetorheologicaldamper[J]. Journal of Vibration and Shock, 2008,27(2):154-156.

[2]陸正剛, 胡用生.基于磁流變阻尼器的鐵道車輛結構振動半主動控制[J].機械工程學報,2006,42(8):95-100.

LU Zheng-gang, HU Yong-sheng. Semi-active control of railway vehicle structural vibrationbased on MR damper[J]. Chinese Journal of Mechanical Engineering, 2006, 42(8):95-100.

[3]涂奉臣, 陳照波, 劉望中,等.新型半主動整星隔振平臺及其模糊最優控制研究[J].振動工程學報, 2010, 23(2):133-139.

TU Feng-chen, CHEN Zhao-bo, LIU Wang-zhong, et al. A new type semi-active whole-spacecraft isolation platform and its fuzzy optimal control[J]. Journal of Vibration Engineering, 2010, 23(2):133-139.

[4]Ok S Y, Kim D S, Park K S, et al.Semi-active fuzzy control of cable-stayed bridges using magneto-rheologicaldampers[J].Engineering Structures, 2007, 29:776-778.

[5]Stanway R, Sproston J L, EI-Wahed A K, Applications of electro-rheological fluids in vibaration control: a survey [J]. Smart Materials and Structures, 1996,5(4): 464-482.

[6]Pang L, Kamath G M, Wereley N M, Analysis and testing of a linear stroke magnetorheological damper[J]. AIAA 98-2040,1998, CP8903(4): 2841-2856.

[7]Spencer Jr B F, Dyke S J, Sain M K, et al. Phenomenological model of a magnetorheological damper [J]. Journal of Engineering Mechanics, ASCE, 1997,123(3):230-238.

[8]Dyke S J, Spencer B F, Sain M K, et al. Modeling and control of magnetorheological dampers for seismic response reduction [J]. Smart Materials and Structures, 1996, 5(5): 565-575.

[9]Choi S B, Lee S K, Park Y P, A hysteresis model for the field-dependent damping force of a magnetorheological damper [J]. Journal of Sound and Vibration, 2001, 245(2): 375-383.

[10]朱曉臨, 數值分析[M]. 合肥: 中國科學技術大學出版社, 2010.

[11]陳恩偉，陸益民，劉正士,等. Taylor展開的線性時變系統參數辨識及誤差分析[J]. 機械工程學報, 2011, 47(7): 90-96.

CHEN En-wei, LU Yi-min, LIU Zheng-shi, et al. Parameter identification and error analysis of linear time varying system based on Taylor expansion[J]. Journal of Mechanical Engineering, 2011, 47(7):90-96.