求解Black-Scholes模型下美式看跌期權的有限差分法
李景詩,王智宇,朱本喜,宋海明
(吉林大學 數學學院,長春 130012)
求解Black-Scholes模型下美式看跌期權的有限差分法
李景詩,王智宇,朱本喜,宋海明
(吉林大學 數學學院,長春 130012)
考慮Black-Scholes模型下美式看跌期權的定價問題.采用有限差分法和Newton法耦合求解Black-Scholes方程,得到了期權價格和最佳實施邊界的數值逼近結果.數值實驗驗證了算法的有效性.
Black-Scholes模型; 美式看跌期權; 最佳實施邊界
0 引 言
Black-Scholes模型在美式期權定價問題中應用廣泛.令S,t,σ,r,q,T和K分別表示原生資產價格、 時間、 原生資產的波動率、 無風險利率、 原生資產的紅利率、 期權的到期日和敲定價格,則美式看跌期權[1]P(S,t)滿足的Black-Scholes模型為
其中:Z+=max{0,Z};B(t)為美式看跌期權的最佳實施邊界,它把美式期權的求解區域分成兩部分,如果S≤B(t),則選擇實施期權,否則繼續持有.
求解Black-Scholes模型下美式看跌期權定價問題目前主要存在以下困難:
1) 求解區域左端的最佳實施邊界B(t)是一條未知曲線,求解區域不規則;
2) 求解區域右端無界,無法直接應用數值算法;
3) 給出的算法需要同時確定期權價格P(S,t)和最佳實施邊界B(t).
針對1),2),本文采用Front-Fixing變換[2-3]和完全匹配層技巧(PML技巧)[4],將問題(1)化成一個有界規則區域上的拋物問題.對于3),本文采用有限差分法和Newton法交替迭代求解截斷后的方程,進而得到期權價格P(S,t)和最佳實施邊界B(t).
1 Front-Fixing變換
由于方程(1)是一個變系數方程,因此為簡化模型,可通過變量替換

將Black-Scholes方程(1)化為一個常系數方程:
其中:
做Front-Fixing變換

則方程(3)可化為
至此解決了第一個難點,將方程(1)的左邊界B(t)化成了x=0的一條直線.注意到,拋物問題(6)是定義在半無窮區域上的,數值求解時需要進行截斷.若直接做人工截斷,則會導致數值不穩定或數值不精確[4].本文采用PML技巧對無界區域進行截斷.
2 PML技巧
下面解決第二個難點.通過PML截斷技巧:
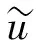

問題(6)可化為如下有界規則區域上的拋物問題:
至此解決了第二個難點.Black-Scholes方程(1)已轉化為一個有界矩形區域上的拋物問題.該問題可以采用有限差分法[5-7]進行數值求解.
3 數值解法
考慮求解方程(9)的數值方法----有限差分法.對方程(9)采用θ格式的有限差分法進行離散化,為此需引入時間剖分:
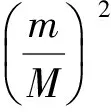
空間剖分:
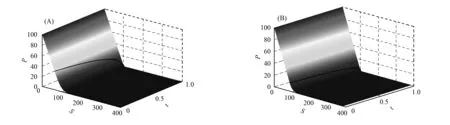
Ih: 0=x0 及差分近似: 方程(9)在點(τm,xn)處對應的θ格式如下: fm為如下向量: 證明: 由b(τ)的定義可知bm<0.下面先證明系數矩陣A是一個M矩陣.當n=1,2,…,N-1時, 當n=0時, 故系數矩陣A為M矩陣. 下面證明右端fm各項均非負.對于固定的m, 由于 采用Newton法求解非線性方程(10),其中 算法如下: 1)b(0)=bm-1-km-1,1 2) 對于j=1,2,… ③ 如果|bj-b(j-1)|≤ε,令bm=b(j),終止循環; 實際計算時,取b0=Kmin(r/q,1),ε=10-6. 考慮對美式看跌期權定價問題(1)進行數值模擬,在方程(1)中,令σ=0.2,K=100,T=1,r和q取以下兩種情形: 1)r=0.05,q=0.05; 2)r=0.1,q=0.01. 為了驗證本文算法得到的數值結果不依賴于θ的選取,對于情形1)和情形2),分別選取不同的θ,數值結果如圖1和圖2所示.其中:t表示時間;S表示股票價格;P表示期權價格.圖1給出了本文算法得到的最佳實施邊界與二叉樹法[8]最佳實施邊界的對比結果.情形1)中取θ=0.5,M=500,N1=1 000,N=1 010,σ0=10,β0=3; 情形2)中取θ=0,M=500,N1=1 000,N=1 010,σ0=10,β0=3; 對于這兩種情形,二叉樹法中都選取M=1 000.圖2給出了兩種情形下本文算法得到期權價格的三維圖像.由數值結果可見,本文算法能較精確地擬合出最佳實施邊界和期權價格. 圖1 本文方法和二叉樹法計算出的最佳實施邊界Fig.1 Optimal exercise boundary of FDM and BM (A) r=0.05,q=0.05; (B) r=0.1,q=0.01. [1]ZHU Songping,ZHANG Jin. A New Predictor-Corrector Scheme for Valuing American Puts [J]. Appl Math Comput,2011,217(9): 4439-4452. [2]Wu L,Kwok Y. A Front-Fixing Finite Difference Method for the Valuation of American Options [J]. J Financial Engineering,1997,6(2): 83-97. [3]Holmes A D,YANG Hongtao. A Front-Fixing Finite Element Method for the Valuation of American Options [J]. SIAM J Sci Comput,2008,30(4): 2158-2180. [4]Lantos N,Nataf F. Perfectly Matched Layers for the Heat and Advection-Diffusion Equations [J]. J Comput Phys,2010,229(24): 9042-9052. [5]Muthuraman K. A Moving Boundary Approach to American Option Pricing [J]. J Economic Dynamics Control,2008,32(11): 3520-3537. [6]HAN Houde,WU Xiaonan. A Fast Numerical Method for the Black-Scholes Equation of American Options [J]. SIAM J Numer Anal,2004,41(6): 2081-2095. [7]姜禮尚. 期權定價的數學模型和方法 [M]. 2版. 北京: 高等教育出版社,2008: 170-191. (JIANG Lishang. Mathematical Modeling and Methods of Option Pricing [M]. 2nd ed. Beijing: Higher Education Press,2008: 170-191.) [8]Barone-Adesi G,Whaley R E. Efficient Analytic Approximation of American Option Values [J]. J Finance,1987,42(2): 301-320. (責任編輯: 趙立芹) FiniteDifferenceMethodforSolvingAmericanPutOptionundertheBlack-ScholesModel LI Jingshi,WANG Zhiyu,ZHU Benxi,SONG Haiming This paper deals with the American put option pricing problem governed by the Black-Scholes equation.Applying finite difference method coupled with Newton’s method to solve the Black-Scholes equation,we can get the numerical approximations of the option price and the optimal exercise boundary simultaneously.Numerical experiments verify the efficiency of the method. Black-Scholes model; American put option; optimal exercise boundary 2013-09-26. 李景詩(1990—),女,漢族,碩士研究生,從事隨機偏微分方程數值解的研究,E-mail: jsli12@mails.jlu.edu.cn.通信作者: 朱本喜(1979—),女,土家族,碩士,講師,從事隨機偏微分方程數值解的研究,E-mail: zhubx@jlu.edu.cn. 國家自然科學基金(批準號: 11271157). O241.8 A 1671-5489(2014)05-0949-05
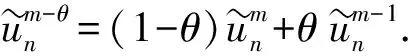
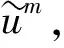




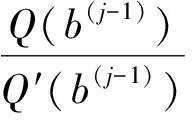

4 數值算例

(CollegeofMathematics,JilinUniversity,Changchun130012,China)

