強序半群的伴隨KS－代數

楊聞起

（寶雞文理學院數學系，陜西 寶雞 721013）

1 預備知識

定義1［1］設S是一個半群，S上有偏序≤，如果?a，b，c∈S，有

則稱S是序半群.如果序半群S還滿足左、右消去律：

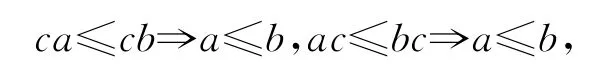
則稱序半群S是強序的.設S是序半群，?≠A?S.如果：

則稱A是序半群S的理想.

1966年，日本數學家K.Iséki以邏輯運算和集合的差運算為背景，引入了BCK－代數和BCI－代數，文獻［2］將其定義簡化.

定義2［2］設集X 上有運算＊及常元0，?x，y，z∈X.如果：

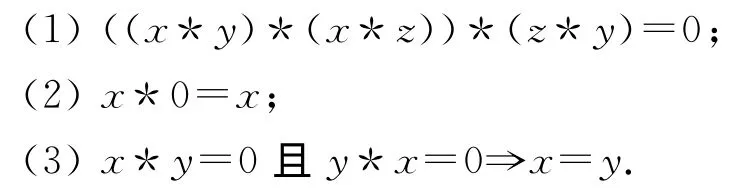
則稱X是一個BCI－代數，記為（X，＊，0），簡記為X.如果BCI－代數X還滿足

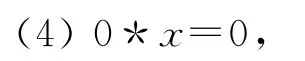
則稱X是BCK－代數.

在BCK（BCI）－代數X中規定：x≤′y?x＊y＝0，那么≤′是X 上的偏序，叫做X的自然偏序，且0為該偏序的最小元（極小元）.

引理1［2］設BCK－代數（X，＊，0）的自然偏序為≤′，那么?x，y，z∈X.有：

（6）0≤′x，即0為該偏序的最小元.

1993年，韓國數學家田英培（Young Bae Jun）等通過在BCK（BCI）－代數上再賦予半群結構，又建立了BCK（BCI）－半群，后來稱為 KS－代數（IS－代數）.文獻［3］系統論述了 KS（IS）－代數理論，文獻［4－5］則給出了IS－代數與半環的關系.

定義3［3］設X是非空集合，它帶有兩種二元運算＊和·及一個常元0.如果：

（1）（X，＊，0）是BCK（BCI）－代數；

（2）（X，·）是半群；

（3）·對＊的左、右分配律成立，即?x，y，z∈X，有

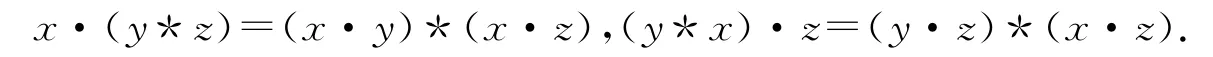
則稱X 關于這兩種運算和常元0是一個BCK（BCI）－半群，也簡稱為 KS－代數（IS－代數），記為（X，＊，·，0），在不致混淆時，簡記為X.為了書寫方便，還把x·y簡記為xy.另外，把BCK－代數（X，＊，0）的自然偏序≤′也叫做KS－代數的自然偏序.

設A是KS－代數（X，＊，·，0）中的非空子集.如果：

（1）?x∈X，?a∈A，有xa，ax∈A；

（2）?x∈X，?a∈A，由x＊a∈A可推出x∈A.稱A是X的I－理想，簡稱為理想.

顯然，KS（IS）－代數（X，＊，·，0）的非空子集A是它的理想當且僅當A 是半群（X，·）的理想且是BCK－代數（X，＊，0）的理想.

引理2［3］在 KS（IS）－代數X 中，≤′是其中的自然偏序，?x，y，x∈X，有：

（1）0x＝x0＝0；

（2）如果x≤′y，那么zx≤′zy，xz≤′yz.

由引理2知，X關于偏序≤′必是一個以0為最小元（極小元）的序半群，稱之為KS－代數的自然序半群.另外，設A是KS－代數（X，＊，·，0）的理想，任取a∈A，則0＝0a∈A，故KS－代數的任意理想都包含0.

偏序集與半群的交融形成了序半群，BCK－代數與半群的交融形成了KS－代數，本文試圖討論序半群與KS－代數的關系.

2 概念和基本性質

那么，（X，＊，·，0）必是一個 KS－代數.

證明 首先，我們證明（X，＊，0）是BCK－代數.任取x∈X，如果0≤x，則0＊x＝0；如果0≤/x，由（1）式也有0＊x＝0.總之，?x∈X，都有0＊x＝0.下面只需驗證（X，＊，0）是BCI－代數.

（1）如果x≤0，由于0為極小元，故x＝0，從而x＊0＝0＝x；如果x≤/0，則x＊0＝x.總之?x∈X，有x＊0＝x.

（2）再任取y，z∈X，如果x≤y，則x＊y＝0，又由于0＊（x＊z）＝0，故得

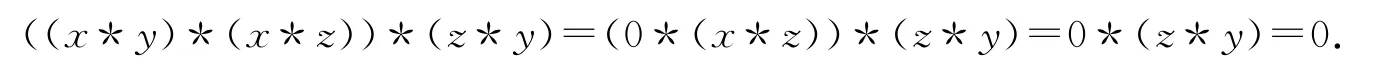
如果x≤/y，但x≤z，則z≤/y，從而x＊y＝x，x＊z＝0，z＊y＝z，有

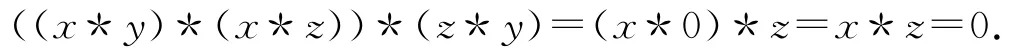
如果x≤/y，且x≤/z，即x＊y＝x，x＊z＝x，有

所以，?x，y，z∈X，都有（（x＊y）＊（x＊z））＊（z＊y）＝0.

（3）如果x＊y＝y＊x＝0，則x≤y或x＝0，且y≤x或y＝0；如果x≤y且y≤x，由于“≤”為偏序，

本文將以0為極小元的序半群記為（X，≤，·，0）.

定理1 在強序半群（X，≤，·，0）中，定義運算＊：故x＝y.如果x≤y，y＝0，由于0是極小元，故x＝0＝y.如果x＝0，y≤x，即y≤0，但0為極小元，故y＝0＝x.如果x＝0，y＝0，顯然x＝y.所以，只要x＊y＝y＊x＝0，就有x＝y.所以（X，＊，0）必是BCK－代數.

其次，我們證明分配律成立.?x，y，z∈X，有：

（1）如果y≤z，即y＊z＝0，則xy≤xz，故x（y＊z）＝x0＝0，（xy）＊（xz）＝0，從而x（y＊z）＝（xy）＊（xz）.

（2）如果y≤/z，則y＊z＝y，即x（y＊z）＝xy.又由于≤是一個強序，從而xy≤/xz，故（xy）＊（xz）＝xy，則x（y＊z）＝（xy）＊（xz）.同理可得（y＊z）x＝（yx）＊（zx），故（X，＊，·，0）必是一個 KS－代數.

定義4 設（X，≤，·，0）是以0為極小元的強序半群，把按照（1）式給出運算＊而得的KS－代數（X，＊，·，0）叫做該強序半群的伴隨 KS－代數，記為（X，＊，·，0）.

由于BCK－代數（X，＊，0）的自然偏序≤′為x≤′y?x＊y＝0，故兩個偏序≤，≤′顯然不同，它們之間的關系如下：

定理2 設強序半群（X，≤，·，0）的伴隨 KS－代數（X，＊，·，0）的自然偏序為≤′，?x，y∈X，x≤′y當且僅當x≤y或者x＝0.

定理3 設（X，≤，·，0）是以0為最小元的強序半群，則它的伴隨KS－代數的（X，＊，·，0）的自然偏序與序半群的偏序一致.

證明 設KS－代數（X，＊，·，0）的自然偏序為≤′，?x，y∈X，設x≤y，由定理2知，x≤′y.反過來，設x≤′y，由定理2知，x≤y或者x＝0，而當x＝0時，由于0為最小元，故0≤y，總之都有x≤y，從而兩個偏序≤，≤′相同.

文獻［1］和文獻［3］分別給出了序半群同構和KS－同構的概念：設f是由序半群（X，≤，·，0）到（X′，≤′，·′，0′）的雙射，如果f既保持乘法又保持偏序，稱f是由（X，≤，·，0）到（X′，≤′，·′，0′）的序半群同構映射；如果有一個雙射f，使f和f－1都是同構映射，稱（X，≤，·，0）與（X′，≤′，·′，0′）是序半群同構.

如果存在 KS－代數（X，＊，·，0）到（X，＊′，·′，0′）的雙射f，使得?x，y∈X，有

稱（X，＊，·，0）與（X，＊′，·′，0′）是 KS－同構.

定理4 設以0為最小元的強序半群（X，≤，·，0）的伴隨KS－代數為（X，＊，·，0），以0′為最小元的強序半群（X′，≤′，·′，0′）的伴隨 KS－代數為（X，＊′，·′，0′），那么，序半群（X，≤，·，0）與（X′，≤′，·′，0′）是序半群同構當且僅當（X，＊，·，0）與（X，＊′，·′，0′）是 KS－同構.

證明 設f是序半群（X，≤，·，0）到（X′，≤′，·′，0′）的序半群同構映射，由于0，0′都是最小元，故f（0）＝0′.?x，y∈X，首先f（x·y）＝f（x）·′f（y），其次有：

（1）如果x≤y，從而f（x）≤′f（y），即x＊y＝0，f（x）＊′f（y）＝0′，故有

（2）如果x≤/y，從而f（x）≤/′f（y），故x＊y＝x，f（x）＊′f（y）＝f（x），則f（x＊y）＝f（x）＝f（x）＊′f（y），故f是（X，＊，·，0）與（X，＊′，·′，0′）的 KS－同構映射.

設f是（X，＊，·，0）與（X，＊′，·′，0′）的 KS－同構映射，則有f（0）＝0′.設x≤y，則x＊y＝0，故f（x）＊′f（y）＝f（x＊y）＝0′.則f（x）≤′f（y），或者f（x）＝0′，如果f（x）＝0′，由于0′為最小元，故也有f（x）≤′f（y），從而f是保序的.同理，f－1也保序.又由于f（x·y）＝f（x）·′f（y），故（X，≤，·，0）與序半群同構.

定理5 設強序半群（X，≤，·，0）的伴隨 KS－代數為（X，＊，·，0），則?x，y，z∈X，有

證明 如果x≤y，那么（x＊y）＊y＝0＊y＝0＝x＊y.如果x≤/y，那么

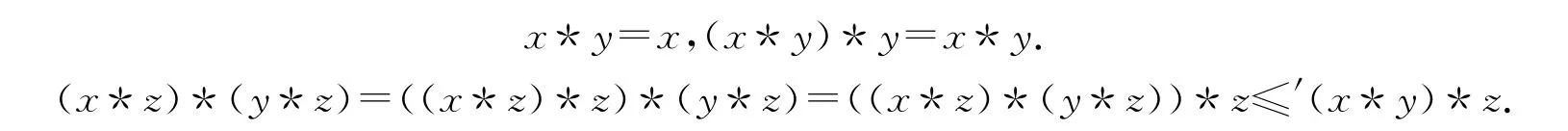
又由于y＊z≤′y，故

3 強序半群及其伴隨KS－代數的理想

定理6 設強序半群（X，≤，·，0）的伴隨KS－代數為（X，＊，·，0），I是X 的非空子集，那么I是強序半群（X，≤，·，0）的理想當且僅當I是伴隨 KS－代數（X，＊，·，0）的理想.

證明 如果I是KS－代數（X，＊，·，0）的理想，設x≤y，且y∈I，則x＊y＝0∈I，從而x∈I，又由于?x∈X，?a∈I，有ax，xa∈I，故I是強序半群（X，≤，·，0）的理想.反過來，如果I是強序半群（X，≤，·，0）的理想，設x＊y，y∈I，若x≤y，則x∈I；若x≤/y，則x＝x＊y∈I，又由于?x∈X，?a∈I，有ax，xa∈I，故I是 KS－代數（X，＊，·，0）的理想.

定理7 設強序半群（X，≤，·，0）的伴隨 KS－代數為（X，＊，·，0），I是半群（X，·）的理想，那么，I是強序半群（X，≤，·，0）的理想當且僅當由（x＊y）＊z∈I，y＊z∈I可推出x＊z∈I.

證明 設I是強序半群（X，≤，·，0）的理想，由定理6知，I必是KS－代數（X，＊，·，0）的理想，設（x＊y）＊z∈I，y＊z∈I，由定理5知，（x＊z）＊（y＊z）＝（x＊y）＊z∈I，由于y＊z∈I，故x＊z∈I.

反過來，設x≤y∈I，則（x＊y）＊0＝x＊y＝0∈I，但是y＊0＝y∈I，故x＝x＊0∈I，所以I是強序半群（X，≤，·，0）的理想.

［1］謝祥云.序半群引論［M］.北京：科學出版社，2001：5－9.

［2］HUANG YISHENG.BCI－algebra［M］.Beijing：Science Press，2006：11－33.

［3］楊聞起.BCI－代數與半群［M］.北京：科學出版社，2011：108－127.

［4］楊聞起.IS－代數的伴隨半環［J］.東北師大學報：自然科學版，2012，44（3）：46－51.

［5］楊聞起.IS－代數的伴侶半環［J］.山東大學學報：理學版，2011，46（12）：66－69.