石墨烯量子點二聚物的等離激元激發

尹海峰, 張 紅, 劉丹丹

(1.凱里學院物理與電子工程學院,貴州凱里556011； 2.四川大學物理科學與技術學院,四川成都610065；3.中原工學院理學院,河南鄭州450000)

自2004年石墨烯的發現以來,石墨烯的可控制備、新奇物理效性的揭示,以及它們的新應用探索等研究內容一直備受關注[1-2],其中,石墨烯等離激元方面的研究尤其受到重視[3].與金屬相比,通過外加靜電場等方法,可以有效、方便地調控石墨烯中的等離激元[3].石墨烯光子器件,可以從太赫茲波段到可見光不同頻率范圍內工作.同時,它還可以把等離激元共振局限于空間很小的區域.利用這一特性,石墨烯有望應用于變換光學,并最終有望應用于光計算和超高速信息處理等領域中的全光邏輯門器件[4].人們目前正在積極探究石墨烯等離激元的共振機制[3],包括用半經驗理論對純石墨烯納米帶等離激元引起的空間局域電場增加的研究[5],經典的電磁理論對純石墨烯納米帶之間表面等離激元耦合特性的研究等[6-7].由于量子尺寸效應,同宏觀二維石墨烯相比,石墨烯量子點具有不一樣的光電特性.已有研究表明,邊界構型[8]和量子點尺寸[9]對石墨烯量子點光電特性有較大影響.大部分吸收光譜峰對應的共振能量,隨著石墨烯量子點的平均尺度增加時,發生單調降低；而對于可見光范圍的光譜,在量子點尺度增加到17 nm時有一個最小值[9].理論上,基于含時密度泛函理論,對于石墨烯量子點等離激元激發的研究表明[10]:由于量子點的尺寸和量子受限效應,在低能共振區,石墨烯量子點的光譜線發生展寬和劈裂.石墨烯量子點的等離激元激發依賴于邊界的構型.沿矩形石墨烯量子點扶手椅邊界方向激發時,低能共振區光譜線發生較大的展寬.此外,對稱性對于石墨烯量子點的等離激元激發也起著重要的作用.沿六角石墨烯量子點所在平面不同方向激發時,吸收光譜線的線形和各吸收峰的強度基本相同.目前,實驗上已經可以制造出不同形狀和摻雜的石墨烯量子點[11-15].

納米顆粒對即量子點二聚物,對量子點二聚物等離激元的研究有助于理解更復雜的量子點之間等離激元的雜化機理.作為一般的特征,文獻[16-18]的研究發現金屬量子點二聚物間存在3種截然不同的相互作用區.當量子點之間的間距較大,二聚物在外場的作用下發生等離激元共振時,由于量子點之間的勢壘較大,2個量子點仍然保持電中性.二聚物中的等離激元共振能量點隨著量子點間距的減小,發生單調的紅移.該相互作用區可以稱為經典作用區.當量子點之間的間距進一步減小,在經典和量子的交叉區域,由于2個量子點間的勢壘降低了,電子可以較容易地隧穿過勢壘,在2個量子點間來回運動,量子效應開始發揮作用.當2個金屬量子點之間的間隙只有幾埃時,在量子點二聚物中電荷轉移等離激元激發模式將會形成[16].該等離激元共振模式隨著間隙的進一步減小發生藍移.由于量子點的等離激元激發特性依賴于量子點的材料和形狀,因此人們開始研究不同形狀和材料的量子點二聚物中表面等離激元的特征[19].到目前為止,還未公開發表關于小尺度石墨烯量子點二聚物等離激元激發的研究結果,所以本文對小尺度石墨烯量子點二聚物的等離激元激發特性進行了理論研究.采用含時密度泛函理論,主要探究隨著間隙改變時,小尺度石墨烯量子點二聚物等離激元激發演變的規律.

1 計算方法

采用含時密度泛函理論計算石墨烯量子點二聚物的吸收光譜,具體是由OCTOPUS軟件來實現[20].與密度泛函理論不同[21-22],含時密度泛函理論計算吸收光譜時,體系的運動方程是電子波函數ψ(r,t)服從的含時Kohn-Sham方程[20]

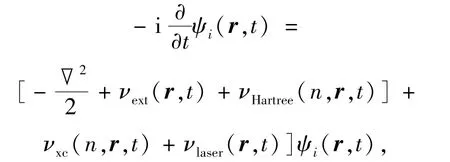
其中,n為電子密度,νHartree為 Hartree 勢,νlaser為作用于體系的外場.在計算中,采用Troullier-Martins形式的模守恒贗勢.對于交換關聯勢νxc,采用局域密度近似(LDA)即

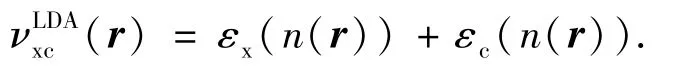
εx和εc分別為每個電子的交換和關聯能,只依賴于r點處的電子密度,等于電子密度為n(r)的均勻電子氣的局域交換關聯能.在計算中,采用文獻[20]提出的具體形式.在激發態計算中,采用絕熱的LDA,νxc(r,t)=νxc(n(r,t)),交換關聯勢只依賴于時刻t的電子密度.

在團簇的基態計算得到電子的占據態信息后,可以通過時間演化波函數的方法來計算電子的激發態.在t=0時刻,使所有波函數有個瞬時的相位移動[23]

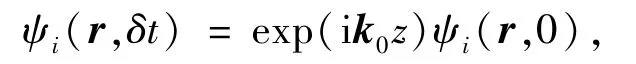
其中,k0為沿z方向所加的微擾外場動量.這相當于加E(t)=k0δ(t)的微擾外場.然后,Kohn-Sham波函數進行時間演化,可以得到含時偶極距d(t).通過對偶極距求傅立葉變換得到動態極化率α(ω),吸收光譜可以用偶極子強度函數S(ω)來表示,它與極化率的關系為

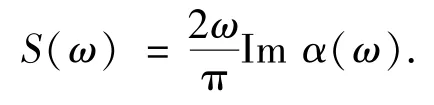
模擬時在每個原子上構建一個球,球的半徑為0.8 nm,模擬空間為每個原子周圍空間的并集.在模擬盒子內使用間距為0.03 nm的均勻格點.時間演化步長為3.3×10-18s,電子波函數的演化總時間為1.98×10-14s.石墨烯邊界處碳原子的懸掛鍵用氫原子進行飽和.此外,還計算了通過石墨烯量子點二聚物間隙處的電流,計算公式為

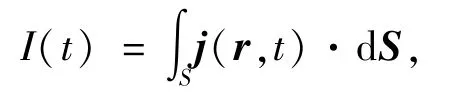
其中,S為間隙處電流通過的一個面,電流密度為

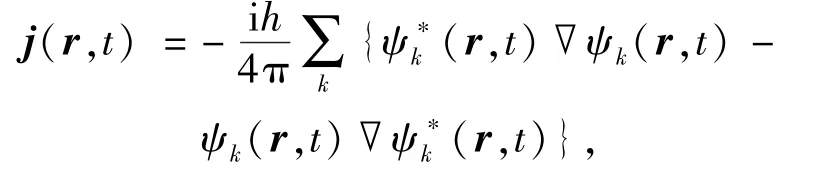
依賴于共振頻率的電流大小(對電流在某些共振頻率做傅立葉變換)公式為

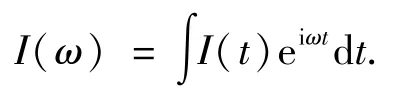
2 結果與討論

采用笛卡爾直角坐標系,石墨烯量子點位于XY平面內.對于具有Z字型邊界的六角形石墨烯量子點,有2條邊平行于Y坐標軸,如圖1所示.對于矩形石墨烯量子點,其Z字型邊界平行于Y坐標軸,如圖2所示.主要討論沿石墨烯量子點所在的平面方向,體系低能共振區的等離激元激發特性.

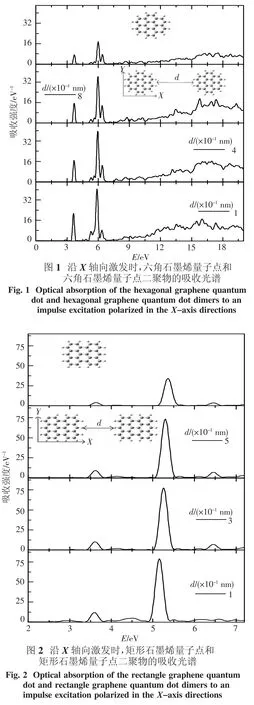
2.1 六角石墨烯量子點二聚物的等離激元激發圖1給出了沿X軸方向,六角石墨烯量子點和六角石墨烯量子點二聚物的吸收光譜.從上向下,六角石墨烯量子點二聚物的間隙分別為0.8、0.4和0.1 nm.圖1為六角石墨烯量子點和六角石墨烯量子點二聚物的結構示意圖.對于尺度較小的六角石墨烯量子點,沿石墨烯量子點所在的平面方向,體系中仍有2個主要的等離激元共振帶[10],其中,一個等離激元共振帶位于能量點16 eV附近,稱為π+σ等離激元；另一個等離激元共振帶位于能量點5 eV附近,稱為π等離激元.同較大尺度的六角石墨烯量子點相比[10],體系中主要的低能共振吸收峰發生了藍移,分別位于3.69和6 eV.這和已有的實驗研究結果一致,隨著石墨烯尺寸的減小,低能區吸收光譜峰對應的共振能量單調增加[24].當間隙d比較大時,2個六角石墨烯量子點之間的相互作用是電容性的,沒有電子可以穿過量子點之間的勢壘.當2個六角石墨烯量子點之間的間隙d=0.8 nm時,其光譜主要的低能吸收峰分別位于3.68和5.98 eV.該結果表明,當2個六角石墨烯量子點靠近,通過電容性的相互作用時,二聚物低能共振區中主要的等離激元共振能量隨著間距的減小發生了紅移,即低能區主要的π等離激元共振模式隨著間距的減小發生了紅移.這種結果和J.Zuloaga等[16]對于金屬量子點二聚物的研究結論一樣.他們也發現當2個量子點之間的距離較大、在經典相互作用區時,二聚物的等離激元共振能量點隨著間距的減小發生紅移.在低能共振區,電容性相互作用時,石墨烯量子點二聚物光譜的線形和單個石墨烯量子點光譜的線形一樣,并且石墨烯量子點二聚物吸收峰的強度約等于單個石墨烯量子點相應吸收峰強度的兩倍.當2個六角石墨烯量子點之間的距離進一步減小時,量子點間的勢壘降低,電子可以隧穿過勢壘,在2個量子點之間運動.與金屬量子點二聚物不同,隨著間隙的減小,雖然在低能共振區,六角石墨烯量子點二聚物光譜吸收峰的強度進一步增加了,但是光譜的線形沒有發生變化[14]；并且,隨著間隙的繼續減小,低能共振區的吸收光譜沒有發生藍移,而是進一步發生了紅移.比如,當間隙d=0.1 nm時,其光譜主要的低能吸收峰分別位于3.62和5.88 eV,即隨著間隙的減小、量子點之間勢壘的降低,電子可以隧穿過勢壘在2個量子點之間運動,在低能共振區,六角石墨烯量子點二聚物中,電容性耦合的等離激元共振模式雖然發生了改變,但共振能量仍然在3.68和5.98 eV附近；六角石墨烯量子點等離激元共振模式之間的耦合較弱.

為了更進一步說明六角石墨烯量子點二聚物低能等離激元共振的物理機制,我們計算了每個共振頻率所對應的誘導電荷密度分布和依賴于共振頻率的電流大小.圖3給出了依賴于共振頻率的電流隨著2個六角石墨烯量子點之間的間隙d的演變過程.計算中電流通過的平面位于2個六角石墨烯量子點中間,與2個六角石墨烯量子點中心的連線垂直.當間隙d比較大時,圖3表明六角石墨烯量子點二聚物的等離激元激發時,2個六角石墨烯量子點保持電中性,相互之間的耦合是電容性的,π電子不能夠在2個六角石墨烯量子點之間來回運動.比如,d=0.6 nm時,其光譜主要的低能吸收峰分別位于3.68和5.97 eV.圖3中與其對應的電流I為零.當間隙d減小,2個六角石墨烯量子點中間的勢壘降低時,電子可以隧穿過中間的勢壘.2個六角石墨烯量子點之間的作用形式發生了改變.當間隙d=0.1 nm時,六角石墨烯量子點二聚物的低能等離激元共振模式對應的電流強度分布,和圖1所示的吸收光譜相對應,即共振強度比較大的等離激元模式對應的電流強度也較大.雖然六角石墨烯量子點二聚物的低能等離激元共振能量變化不大,但是由于電子的隧穿,二聚物的等離激元共振模式發生了變化,已經不再是電容性相互作用.實際上,由于電子隧穿,電容性耦合的等離激元共振模式逐漸演變成另外一種新的等離激元共振模式.這種新的等離激元共振模式可以看作是長程電荷轉移激發共振模式和電容性耦合等離激元共振模式的雜化耦合結果.

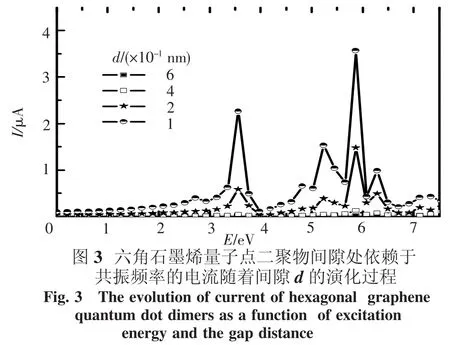
圖4分別給出了單個石墨烯量子點(圖4(a))和間隙為0.1 nm的六角石墨烯量子點二聚物(圖4(b)),在能量為3.69和3.62 eV的等離激元傅立葉變換誘導電荷密度分布.傅立葉變換的誘導電荷密度計算公式為

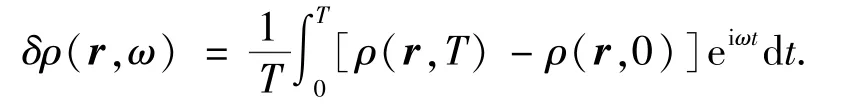
通過變換,可以得到該頻率集體激發所對應電荷的空間分布.圖4給出的誘導電荷密度平面平行于石墨烯量子點所在的平面,兩平面間的垂直距離為0.09 nm.對于單個六角石墨烯量子點,該等離激元共振模式的誘導電荷密度分布在量子點的邊緣區域,具有類偶極子共振的特征.這主要是由于單個石墨烯量子點低能區的等離激元激發是一種長程電荷轉移激發,沿激發方向,電子可以在很長一段距離內來回振動[10].圖4(b)是在2個六角石墨烯量子點之間的間隙較小時,3.62 eV處低能等離激元共振模式對應的誘導電荷密度分布.該等離激元共振模式的誘導電荷密度分布,類似于2個單獨排列的六角石墨烯量子點在3.69 eV處等離激元共振模式對應的誘導電荷密度分布.雖然量子點間的勢壘降低了,圖4(b)的結果再次表明,大部分π電子仍然主要在單個量子點中振動.由于間隙較小時,少部分電子可以隧穿過量子點間的勢壘,在2個量子點之間運動,所以2個六角石墨烯量子點之間的耦合形式發生了變化,形成了一種新型的雜化等離激元共振模式.參與該雜化等離激元共振模式的大部分電子分別在2個石墨烯量子點中來回振動,少部分電子在2個石墨烯量子點之間來回振動.與金屬納米結構二聚物相比,石墨烯量子點間的耦合作用較弱.對于不同的間隙,在3.65 eV附近,六角石墨烯量子點二聚物中主要存在如圖4(b)所示的這種等離激元共振模式.

2.2 矩形石墨烯量子點二聚物的等離激元激發圖2給出了沿X軸方向,矩形石墨烯量子點和矩形石墨烯量子點二聚物的吸收光譜.從上向下,矩形石墨烯量子點二聚物的間隙分別為0.5、0.3和0.1 nm.插圖為矩形石墨烯量子點和矩形石墨烯量子點二聚物的結構示意圖.對于單個矩形石墨烯量子點,沿扶手椅方向激發時,體系中主要的低能共振吸收峰分別位于3.63和5.36 eV.對于矩形石墨烯量子點二聚物,當間隙d比較大時,2個量子點之間的相互作用是電容性的,沒有電子可以穿過量子點之間的勢壘.在間隙d=0.5 nm,沿扶手椅方向激發時,其光譜主要的低能吸收峰分別位于3.62和5.3 eV.同六角石墨烯量子點二聚物一樣,當矩形石墨烯量子點靠近,通過電容性的相互作用時,二聚物低能共振區中主要的等離激元共振能量隨著間距的減小發生了紅移.隨著間隙繼續減小,量子點間的勢壘降低,電子可以隧穿過勢壘,在2個量子點之間運動.在低能共振區,矩形石墨烯量子點二聚物光譜吸收峰的強度進一步增加了,光譜的線形同樣沒有發生變化；并且,隨著間隙的繼續減小,低能共振區的吸收光譜也進一步發生了紅移.由于電子隧穿,電容性耦合的等離激元共振模式逐漸演變成雜化等離激元共振模式.這種新的等離激元共振模式是長程電荷轉移激發共振模式和電容性耦合等離激元共振模式的雜化耦合結果.與六角石墨烯量子點二聚物不同的是,隨著間隙的減小,矩形石墨烯量子點二聚物在低能共振區2.92 eV附近出現了一些強度較弱的吸收峰.這種區別主要來源于石墨烯量子點形狀不同引起的.

3 結論

用含時密度泛函理論系統地研究了,隨著2個石墨烯量子點間的間距改變時,六角石墨烯量子點二聚物和矩形石墨烯量子點二聚物等離激元共振模式的演化規律.通過對計算結果的分析,得出以下主要結論.對于大的間隙,由于石墨烯量子點之間的勢壘較大,π電子很難穿過勢壘,二聚物中2個石墨烯量子點之間存在電容性的相互作用.在低能共振區,與金屬納米結構二聚物相同,石墨烯量子點二聚物的等離激元共振能量隨著間隙的減小也發生了紅移.當間隙進一步減小時,由于2個石墨烯量子點之間的勢壘降低,電子可以隧穿過勢壘在2個石墨烯量子點之間來回運動.對于小的間隙,吸收光譜、誘導電荷密度分布以及依賴于共振頻率的電流分布表明,在石墨烯量子點二聚物中形成了雜化等離激元共振模式.該等離激元共振模式可以看作是長程電荷轉移激發共振模式和電容性耦合等離激元共振模式的雜化耦合結果.與金屬納米結構二聚物中的長程電荷轉移激發模式不同,石墨烯量子點二聚物中的雜化等離激元共振模式,隨著間隙繼續減小時并沒有發生藍移,而是繼續紅移.此外,隨著間隙改變時,不同形狀石墨烯量子點二聚物等離激元共振模式的演化規律基本相同,不依賴于石墨烯量子點的形狀.石墨烯量子點等離激元共振模式之間的耦合較弱.

致謝感謝凱里學院規劃課題基金(BS201301和Z1308)對本研究給予資助,謹致謝意.

[1]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.

[2]曾暉,趙俊,韋建衛,等.含有碳鏈通道的石墨烯納米帶電子特性的第一性原理研究[J].四川師范大學學報:自然科學版,2013,36(1):87-91.

[3]Grigorenko A N,Polini M,Novoselov K S.Graphene plasmonics[J].Nature Photonics,2012,6(11):749-758.

[4]Vakil A,Engheta N.Transformation optics using graphene[J].Science,2011,332(6035):1291-1294.

[5]Cocchi C,Prezzi D,Ruini A,et al.Optical excitations and field enhancement in short graphene nanoribbons[J].J Phys Chem Lett,2012,3(7):924-929.

[6]Christensen J,Manjavacas A,Thongrattanasiri S,et al.Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons[J].ACS Nano,2012,6(1):431-440.

[7]Ong Z Y,Fischetti M V.Theory of interfacial plasmon-phonon scattering in supported graphene[J].Phys Rev,2012,B86(16):165422.

[8]Ritter K A,Lyding J W.The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons[J].Nature Materials,2009,8(3):235-242.

[9]Kim S,Hwang S W,Kim M K.Anomalous behaviors of visible luminescence from graphene quantum dots:interplay between size and shape[J].ACS Nano,2012,6(9):8203-8208.

[10]Yin H F,Zhang H.Plasmons in graphene nanostructures[J].J Appl Phys,2012,111(10):103502.

[11]Li M,Wu W,Ren W,et al.Synthesis and upconversion luminescence of N-doped graphene quantum dots[J].Appl Phys Lett,2012,101(10):103107.

[12]Jin S H,Kim D H,Jun G H,et al.Tuning the photoluminescence of graphene quantum dots through the charge transfer effect of functional groups[J].ACS Nano,2013,7(2):1239-1245.

[13]Yan X,Cui X,Li B S,et al.Large,solution-processable graphene quantum dots as light absorbers for photovoltaics[J].Nano Lett,2010,10(5):1869-1873.

[14]Yan X,Cui X,Li L.Synthesis of large,stable colloidal graphene quantum dots with tunable size[J].J Am Chem Soc,2010,132(17):5944-5945.

[15]Li Y,Zhao Y,Cheng H,et al.Nitrogen-doped graphene quantum dots with oxygen-rich functional groups[J].J Am Chem Soc,2012,134(1):15-18.

[16]Zuloaga J,Prodan E,Nordlander P.Quantum description of the plasmon resonances of a nanoparticle dimer[J].Nano Lett,2009,9(2):887-891.

[17]Song P,Meng S,Nordlander P,et al.Quantum plasmonics:symmetry-dependent plasmon-molecule coupling and quantized photoconductances[J].Phys Rev,2012,B86(12):121410.

[18]Song P,Nordlander P,Gao S W.Quantum mechanical study of the coupling of plasmon excitations to atomic-scale electron transport[J].J Chem Phys,2011,134(7):074701.

[19]Tsai C Y,Lin J W,Wu C Y,et al.Plasmonic coupling in gold nanoring dimers:observation of coupled bonding mode[J].Nano Lett,2012,12(3):1648-1654.

[20]Marques M,Castro A,Bertsch G F,et al.Octopus:a first-principles tool for excited electron-ion dynamics[J].Comput Phys Commun,2003,151(1):60-78.

[21]李雪梅,李權,趙可清.外場作用下含羥乙基活性基團的噻唑生色分子的光譜和二階非線性光學性質[J].四川師范大學學報:自然科學版,2010,33(2):231-234.

[22]劉芳玲,張紅梅,廖顯威.萘及其1-鹵素取代化合物的熒光光譜的量子化學研究[J].四川師范大學學報:自然科學版,2009,32(4):490-492.

[23]Yabana K,Bertsch G F.Time-dependent local-density approximation in real time[J].Phys Rev,1996,B54(7):4484.

[24]Kim S,Hwang S W,Kim M K,et al.ACS Nano,2012,6(9):8203-8208.