一種利用旋轉編碼器的車輛姿態動態算法研究*

李明喜，項昌樂，賈 鵬，袁 一

(1.北京理工大學機械與車輛學院，北京 100081;2.軍事交通學院汽車工程系，天津 300161)

前言

智能車輛(Intelligent Vehicle)路徑跟蹤控制是其研究領域的熱點問題，研究重點之一是實時確定或測量智能車輛自身的位置和姿態，為控制系統提供準確的反饋信號［1－3］，實現路徑跟蹤、障礙規避、超車換道、通過復雜路況、自動泊車等常規駕駛行為［4－6］。目前確定車輛自身位置和姿態的方法通常有兩大類［7］:一類是從全球定位信號，如GPS和北斗定位系統等獲得信息;另一類是利用雷達或攝像機識別智能車輛周圍某一典型特征(如車道線)作為參照物，實現自身定位。這些方法存在定位精度低、實時性差的缺陷，并且受橋梁、涵洞或高大建筑物遮擋的影響，不適合在城市道路環境中使用［6，8］;同時雷達、攝像機等極易受到光照、霧、路面反射率變化的影響而失效［9］;本文中采用左右車輪的編碼器信號測量左右車輪滾動距離，實時計算車輛在初始坐標系中一段時間內的車輛位置和行駛方向的方法。文獻［8］和文獻［10］中也對該方法進行了研究，但僅限于幾何運動關系的分析，并忽略了復雜的輪胎側偏特性，因此在輪胎側偏現象明顯的彎道工況下，計算結果存在較大誤差。而彎道行駛車輛姿態的準確測量是智能車輛實現控制的關鍵要求。

本文中重點研究考慮輪胎側偏特性時的計算方法，使該方法適合于較高車速彎道行駛時姿態的確定，且不受周圍環境變化的影響，為智能車實現路徑規劃和路徑跟蹤控制提供了重要的基礎條件。

1 問題的描述

智能車輛在行駛過程中，假設已知條件是在固定采樣周期T下，左右車輪中心向前移動的距離分別通過旋轉編碼器測量輸出的脈沖數測得，左右車輪的脈沖讀數分別構成兩個有限序列EL、ER:

式中i為采樣序號。

在已知車輛的結構參數輪距B、軸距L、輪胎型號、前后軸軸荷Mf、Mr的條件下，尋求一種算法，求解每個采樣周期內車輛4個車輪中心的坐標位置序列Θ和車輛航向角序列ψ:

式中j為車輪序號。

顯然若獲得序列Θ和ψ，即可獲得車輛的運動軌跡和方位，若智能車輛控制決策系統所規劃的行駛路徑轉換到相同坐標系下，即可實時獲得車輛行駛軌跡與規劃路徑之間的姿態偏差，是智能車輛進行路徑跟蹤控制的重要依據。

2 智能車輛姿態計算方法

車輛在行駛過程中，其行駛軌跡通常是連續的光滑曲線，具體到每一個微小的位移段，可以認為車輛在該位移段做勻速圓周運動，因而可假設車輛的實際行駛軌跡是由有限段不同長度的圓弧首尾連接組合構成。考慮后輪通常為非轉向車輪，與車身的相對位置關系變化不大，分別測量左右兩側車輪的滾動距離和滾動速度，利用運動學關系，獲得確定每段圓弧的參數r和θ的方程，即可求得車輛位置和航向信息。

2.1 左右車輪側偏角與左右車輪平移速度的關系

由于輪胎彈性，車輪在滾動過程中必然存在側偏現象，車輪同時存在縱向運動u和側向運動v。依據運動關系可得左、右車輪的側偏角β1、β2為

考慮后軸左右車輪通過車軸連結在一起，在車軸軸線方向上的側向運動速度必然相等，即有

2.2 后軸總側偏力與左右車輪平移速度的關系

由于作用在后軸的總側偏力為彎道行駛的車輛后軸質量產生的向心力在車身側向的分量，考慮左右車輪測得的速度為輪胎實際速度在x軸上的分量，即 u1、u2，故車輛橫擺角速度為

后軸側向加速度為

故后軸總側偏力為

2.3 后軸總側偏力與左右車輪側偏角的關系

根據側偏特性，后軸左右車輪的側偏角為

式中:Fy1、Fy2為車輛后軸左右車輪的輪胎側偏力;K為輪胎的側偏剛度(考慮其在線性范圍之內［11］)。

2.4 后軸側向速度和左右輪側偏角的計算

同時由式(3)和式(4)可得后軸側向速度v為

2.5 車輛行駛軌跡和航向角的確定

下面分析求解車輛行駛時每個車輪中心點在地面的投影坐標和車輛的實際航向角。為了描述方便，在算法初始化時確定車輛的坐標系(見圖1)，原點O位于后軸中心在地面的投影，X軸方向為此時車輛的縱軸線方向，向前為正;Y軸水平向右為正，依據右手定則，Z軸垂直向下為正。此坐標系與大地固定在一起，只要計算過程不重新初始化，此坐標系就一直不變，忽略車輛在Z軸方向的小幅運動。

因而在初始化狀態下，車輛的航向角ψ0=0;后軸車輪中心在地面的投影坐標分別為

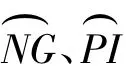
因此在下一個采樣周期開始時，后軸左右車輪中心在虛擬坐標系內的坐標變化量為

車輛的航向角增量為θ。

若車輛的初始位置在初始的虛擬坐標系中的坐標與前述一致，則在下一個采樣周期開始時，后軸左右車輪中心在虛擬坐標系內的坐標位置為

車輛的航向角ψ1=θ。

前軸左右車輪的坐標可以后軸左右車輪的坐標為基礎做簡單的平移計算即可得到。在后續的采樣周期中，后軸左右車輪中心點在地面投影的坐標和車輛航向角的計算思路與前述過程一致，這里不再贅述，則可求得車輛姿態序列Θ和ψ。

3 輸入參數的測量與獲取

分析本文的方法可知，要完成姿態計算，須測量左右車輪在一個采樣周期內車輪滾過的弧長和該周期內左右車輪的縱向速度。

理論上車輪在滾動過程中，由于輪胎的彈性，實際滾動的距離受車輪滾動半徑和車輪滾動角位移的影響，計算公式為s=2πRrN，式中N為車輪滾動的轉數，可由左右輪的旋轉編碼器準確測量，Rr為車輪滾動半徑，該參數主要受輪胎結構、充氣壓力、切向力和輪胎垂向載荷的影響［12－13］，對于某一車輛，前兩個影響因素基本確定，可通過合適的標定方法來確定車輪的滾動半徑:

式中:S為標定距離;NP為車輪轉動一周編碼器脈沖讀數;Ec為標定距離內編碼器脈沖增量。

為消除輪胎切向力的影響，尤其是驅動力對輪胎滾動半徑的影響，將編碼器安裝在非驅動車輪上，可有效消除驅動力對車輪滾動半徑Rr的影響，轎車通常都采用前輪驅動，故將編碼器安裝在后輪上。

輪胎的滾動半徑受垂向載荷的影響，車輛在直線行駛時，左右車輪垂向載荷基本不變，而在彎道行駛，尤其是在高速行駛時，會引起左右車輪垂向載荷的轉移，其特征是內側車輪減少ΔFz，外側車輪增加ΔFz，增加和減少的值相等，同時取決于側向加速度ay的大小［12］。故:

若假定垂向載荷增量ΔFz與滾動半徑變化量為簡單線性關系［13］，線性因子為γ。

車輪滾動半徑的修正因子為

式中γ為車輪滾動半徑與垂向載荷的相關因子，通過輪胎在轉鼓試驗臺上測定。

因此左右車輪滾動的弧長ΔS為

式中E'n為車輪編碼器讀數增量。

左右車輪輪速可由旋轉編碼器直接輸出，也可通過計算得到:

式中T為采樣周期。

4 實驗驗證

為測試算法的有效性，在某轎車上進行了實驗驗證。車輛主要參數如下:軸距L=2.63m，輪距B=1.54m，輪胎型號 215/65R16，整車質量 M=1 550kg，前軸載荷質量 Mf=1 033kg，后軸載荷質量Mr=417kg，編碼器型號 E6B2－C，采樣周期 T=10ms，實驗場地為近似矩形道路，運行一周，保證車輛起點與終點位置相同，航向角相同，總實驗行程658m，平均行駛速度10km/h，采集有效數據1 827條。

圖2～圖4中A曲線為忽略輪胎側偏特性時計算結果和偏差情況。圖2中A曲線為車輛行駛軌跡的計算結果，計算軌跡的起點與終點存在一定的偏差。圖3中A曲線顯示計算軌跡與實際行駛軌跡間的偏差變化情況，可以得出兩個結論:(1)隨著行駛距離的增長，積累誤差隨之增大;(2)計算軌跡的偏差在658m的行程后，最大偏差達到8m。圖4中A曲線顯示了航向角的偏差變化，也反映兩個問題:(1)車輛直線行駛狀態下，航向角的偏差變化不大;(2)車輛在轉彎過程中，航向角的偏差出現較大增加。最終航向角的偏差達到5°左右。上述結果反映了在不考慮輪胎側偏特性時，導致軌跡計算的較大偏差，表現為車輛航向角增長偏快，原因分析:通常車輛因輪胎側偏特性都表現出不足轉向特性，忽略側偏特性就等于加快了車輛航向角的增長，此處的計算結果與理論分析一致。

圖2～圖4中B曲線為考慮輪胎側偏現象時計算結果和偏差情況。可以明顯得到，在圖2中顯示的B曲線計算軌跡的起點與終點位置基本重合，其偏差在圖3中B曲線顯示只有1.65m;航向角的最大偏差在圖4中B曲線顯示小于1°。起點與終點的偏差和航向角的偏差均約減小至原來的1/5。

圖2中C曲線為采用GPS信號記錄的車輛位置信息，該信息不僅不穩定，而且在有高大建筑物的遮擋時信號嚴重偏離實際道路中心線，與車輛行駛軌跡跟蹤控制的精度要求相差甚遠。此外在實驗過程中，當車輛進入涵洞，GPS信號將完全丟失，造成車輛定位盲區，容易引發危險。

上述實驗數據證明:輪胎側偏特性對車輛的行駛姿態有較大影響，考慮側偏特性的計算方法能夠提高車輛行駛姿態計算的準確度，可滿足智能車輛在實時車輛軌跡跟蹤和路徑規劃的要求。

本文的計算方法已在智能車完成京津高速全線無人駕駛實驗任務中得到實際驗證。

5 結論

(1)利用后軸左右車輪旋轉角位移，能夠實時確定車輛的行駛位置和行駛方向。

(2)利用后軸左右車輪旋轉角速度，確定車輛后軸側偏角和側向速度，提高了車輛的行駛位置和行駛方向的計算準確度。

該方法不依賴于外部參照物或全球定位系統，僅依靠自身傳感器的數據，需要輸入的數據量小、獲取成本低，不受涵洞、高大建筑、光照、霧、雨等周圍環境變化的影響。采用疊加計算方式，計算量小，內存占用小，滿足實時控制的要求。

［1］ Petriu E M，Basran J S．On the Position Measurement of Automated Guided Vehicles Using Pseudorandom Encoding［J］．Instrumentation and Measurement，IEEE Transactions on，1989，38(3):799－803．

［2］ Krysik P，Kulpa K，Baczyk M，et al．Ground Moving Vehicles Velocity Monitoring Using a GSM Based Passive Bistatic Radar［C］．Radar，2011 IEEE CIE International Conference on．Chengdu:IEEE，2011．

［3］ Buda W，Dorau T，Lukwinski D，et al．Performance of Track Formation Algorithms Using Radar Measurements Influenced by Urban Environment［C］．Radar Symposium(IRS)，2011 Proceedings International．Leipzig:2011．

［4］ Jiayuan Z，Yumin S，Yulei L．Unmanned Surface Vehicle Target Tracking Based on Marine Radar［C］．Computer Science and Service System(CSSS)，2011 International Conference on．Nanjing:IEEE，2011．

［5］ Chuanli N，Shengrui Z．Traveling Trace Simulation Model for Left Turn Vehicles Based on Stop Line［J］．Computer Engineering and Applications，2009，45(9):24 －27．

［6］ Shiu H T，Hall P S，Hoare E G，et al．Advance Path Measurement for Automotive Radar Applications［C］．Intelligent Transportation Systems，IEEE Transactions on，2006:273 －281．

［7］ Petriu E M，Basran J S，Groen F C A．Automated Guided Vehicle Position Recovery［J］．Instrumentation and Measurement，IEEE Transactions on，1990，39(1):254 －258．

［8］ Feng L，Zhihui H，Fei Y，et al．Route Memorization in Real-time Data Processing Using Run-Length Encoding［C］．Intelligent Vehicles Symposium，2009 IEEE．Xi'an:2009．

［9］ Maresca S，Greco M，Gini F，et al．Radar Tracking of a Maneuvering Ground Vehicle Using an Airborne Sensor［C］．Radar Conference-Surveillance for a Safer World，2009．RADAR．International．Bordeaux:IEEE，2009．

［10］ Petriu E M．Automated Guided Vehicle with Absolute Encoded Guide-path［J］．Robotics and Automation，IEEE Transactions on，1991，7(4):562 －565．

［11］ Carlson C R，Gerdes J C．Consistent Nonlinear Estimation of Longitudinal Tire Stiffness and Effective Radius［C］．Control Systems Technology，IEEE Transaction，2005．

［12］ Tannoury C E，Plestan F，Moussaoui S，et al．Tyre Effective Radius and Vehicle Velocity Estimation:A Variable Structure Observer Solution［C］．Systems，Signals and Devices(SSD)，2011 8th International Multi-Conference on．Sousse:IEEE，2011．

［13］ Shraim H，Rabhi A，Ouladsine M，et al．Estimation and Analysis of the Tire Pressure Effects on the Comportment of the Vehicle Center of Gravity［C］．Variable Structure Systems，2006．VSS'06．International Workshop on．Alghero，Sardinia:2006．