加速度計I/F變換電路數字補償方法

黃麗娟，邵志浩，鄭永強，李 麗

（湖北航天技術研究院 總體設計所，武漢 430040）

加速度計I/F變換電路數字補償方法

黃麗娟，邵志浩，鄭永強，李 麗

（湖北航天技術研究院 總體設計所，武漢 430040）

石英撓性加速度計的輸出 I/F變換電路存在分辨率與線性度互為矛盾的現象，也是目前困擾國內慣導產品精度提升的普遍問題。文中通過對現有 I/F變換電路的電路原理、影響輸出分辨率和線性度的主要原因、電路中元器件的參數特性等進行了詳細分析，提出了一種全新的數字補償算法，可以在不改變現有硬件的基礎上，用軟件實現線性度的算法補償，并給出了完整的數字補償計算公式和各參數的獲取方法。經過慣導產品的試驗驗證，該算法可以使 I/F變換電路的線性度提高一個數量級。I/F變換電路數字補償算法不僅有效解決了電路分辨率與線性度互為矛盾的問題，且易于實現，同時還可以大大簡化生產中繁瑣的硬件調試過程，具有較高的工程應用價值。

慣導系統；石英撓性加速度計；I/F變換；線性度；數字補償

慣導系統的精度是飛行器的重要指標，也是提高飛行器應用能力的關鍵內容之一。其中，敏感彈體線速度的重要部件為加速度計，目前國內慣導產品中應用較成熟廣泛的加速度計是石英撓性加速度計。石英撓性加速度計輸出與敏感軸加速度成正比的電流信號，該電流信號需要經相應處理后最終得到敏感軸方向的加速度。常用的電流測量方法包括I/F變換、V/F變換[1]、A/D轉換[2]、調寬脈沖反饋[3]等方法。其中I/F變換對輸入電流信號進行積分，對噪聲具有平滑抑制作用，具有良好的抗干擾性能，在加速度計信號處理方面得到廣泛應用。

國內石英撓性加速度計批量生產可以達到的精度水平約為：分辨率10 μg、線性度1.0E-05。實際設計中，受 I/F變換電路中相關元器件參數、輸出量程等因素的影響，無法同時保證全量程輸出的線性度與轉換后的實際分辨率，為國內慣導產品I/F變換電路普遍存在的問題[7-8]。目前常用解決方法包括：一種是先降低I/F變換電路轉換頻率，保證I/F變換電路線性度；后級增加A/D轉換電路，對I/F變換電路輸出的脈沖信號進行細分處理，提高小信號的輸出實時性[4]。另一種是對輸出脈沖與輸入電流進行多項式擬合，然后通過軟件進行補償[5]。

上述第一種方法已經應用到成熟產品上，確實大大提高了加速度計通道的輸出當量。但因為 I/F變換電路的積分波形在動態時很不規則，導致動態信號在A/D 轉換時會出現較大誤差，因此，在設計中為了避免A/D的動態輸出誤差，仍然采用I/F變換電路的輸出脈沖來保證最終輸出脈沖數的正確性。也就是說，在動態時，慣導系統加速度計通道的實際輸出分辨率仍然由I/F變換電路的轉換頻率來決定。該方法可以在一定程度上提高加速度計的靜態分辨率，卻降低了動態信號的分辨率，特別是在動態小信號應用場合（如發射前的初始調平、飛行過程中的小推力滑行等）時，加速度計通道的輸出存在明顯地跳變現象。

本文通過對現有 I/F變換電路的電路原理、影響輸出當量的主要原因、元器件的參數特性等進行了詳細分析，提出了一種有效的數字補償算法，該算法可以在不改變現有硬件電路、不增加額外器件的基礎上，在一定程度上解決 I/F變換電路分辨率與線性度互為矛盾的問題，從而達到提高慣導產品加速度計通道精度的最終目的。

1 I/F變換電路機理分析

1.1 I/F變換電路原理

I/F變換電路包括基本恒壓源、正負通道恒流源、積分電路、電壓比較及脈沖輸出電路、充放電回路、頻標電路等幾部分組成，電路原理框圖見圖1。

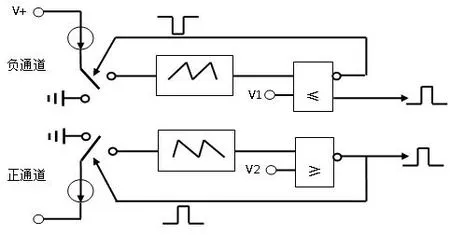
圖1 I/F變換電路原理框圖Fig.1 Schematic of I/F converter

以正向通道為例，I/F變換電路的工作過程是：加速度計輸出的電流進入到積分器的輸入端，在積分器的輸出端得到積分鋸齒波，當鋸齒波幅值達到設定電壓門檻值時，電壓比較電路的輸出端輸出一個脈沖信號（脈沖信號的寬度是頻標頻率的周期）；同時，這個脈沖信號啟動放電回路控制，通過恒流源泄放積分器中的電量，放電時間也是頻標頻率的周期，之后電壓比較電路的輸出端翻轉，結束一個脈沖的轉換。

1.2 電路輸出的非線性問題

通過對電路輸出脈沖數進行測試與分析發現，I/F變換電路中，輸出量程的前半段線性度較高（圖2所示的K前）；在量程的一半時出現一個拐點，后半段出現另一個斜率（圖2所示的K后），使整個量程內線性度較差。

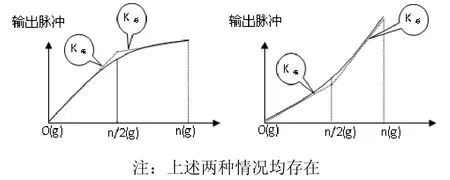
圖2 電路板輸出線性度測試情況示意圖Fig.2 Output linearity test

在實際測量中還發現，電路設計的頻標頻率越高、線性度越差，這也就是前面所說的線性度與分辨率（當量）不能同時保證的問題。且量程越大，上述矛盾越明顯。

1.3 影響輸出的原因及機理分析

加速度計的輸出電流到I/F變換電路的積分器積分，當積分電壓達到一定幅值后，由比較電路控制充放電回路中的開關三級管導通（或截止），從而使恒流源（I0）向積分器充電（或放電），充電（或放電）的時間T固定，得到Q＝I0·T，這個過程即得到一個量化后的脈沖（也可以理解為一個電量單位Q）。在理想情況下，一個電量單位的電量Q= I0·T，見圖3所示陰影區域的面積(Q)。

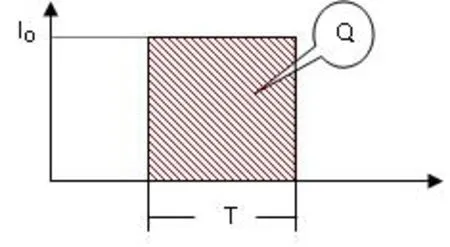
圖3 理想狀態下的一個電量單位Fig.3 Theoretical electric quantity

經過對電路各關鍵電路、各元器件的參數及實測數據進行研究分析發現，在一定的頻率范圍內，I/F變換電路中影響輸出線性度的主要因素是充放電回路中的開關三級管[6]。這是因為開關三極管在導通和截止時，都有一定的沿寬，且前后沿寬不相等，這就導致電量單位Q≠Q＇(見圖4所示，Q為一個理想的電量單位，見右斜線陰影面積；Q＇為實際轉換的電量單位，見左斜線陰影面積；中間為二者重疊部分)。

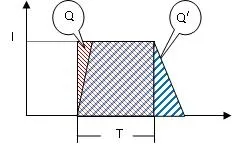
圖4 實際與理想狀態下的電量單位對比示意圖Fig.4 Comparison between theoretical and real electric quantity

由此可以分析出如下結論：假定在一段時間內輸入的電量為q，理想狀態下轉換的脈沖數應為 N=q/Q；因為電路中存在轉換誤差，實際上得到的脈沖數N＇≠N。

另外，積分器的輸出波形又與輸入的電流大小有關。以26 mA（約20g）的設計量程為例，在加速度電流為1 mA、8 mA、13 mA、20 mA、25 mA時，積分波形、比較輸出的脈沖波形如圖5所示。

假定電路中的最大輸入加速度電流為I0(即電路設計的最大量程，圖5中為26 mA），ΔQ＝Q＇－Q，根據上述兩方面的現象，可以得到如下分析結果：

A） 輸入的加速度電流i1＜i2≤I0/2（即不大于全量程的一半）

在一定時間t內，i1、i2充電（或放電）周期個數分別與對應的輸出脈沖個數N1、N2相同，也即開關電路的翻轉次數M1＝N1、M2＝N2。因此，時間t內的電量q1、q2為：

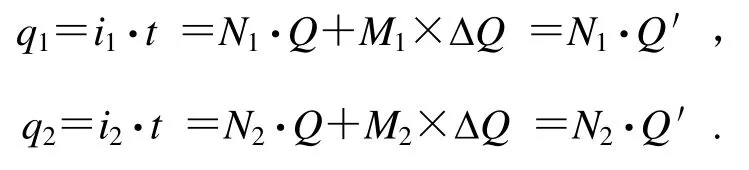
有N1／N2＝ i1／i2也就是說，轉換后的脈沖數仍然呈線性關系，只是斜率與理想狀態不同。

B） 輸入加速度電流I0/2＜i1＜i2＜I0（即大于全量程的一半）

在一定時間t內，i1、i2充電（或放電）周期個數與對應的輸出脈沖個數不相同，開關電路的翻轉次數M1＜N1、M2＜N2；且隨著電流的增大，翻轉次數在遞減，即M2＜M1。因此，時間t內的電量q1、q2為：

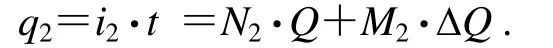
有 N1／N2＜i1／i2（當ΔQ＞0時）或 N1／N2＞i1／i2（當ΔQ＜0時）。也就是說，輸入不同電流的比值與轉換后脈沖數的比值已經不是完全的線性關系。

圖5 在不同輸入加速度電流時的積分波形、輸出脈沖波形Fig.5 Integral curves and output pulses for different current inputs

2 補償算法

可以根據上述分析結果，找到一種數字補償算法，得到一個近似于理想狀態的新斜率，見圖6所示的K＇。

線性度補償算法的基本思路是：因為只有在輸出波形出現一個上升沿和下降沿對時，才會出現一個ΔQ＝Q＇－Q；當過程中開關管沒有出現翻轉時，認為一個脈沖的電量仍然為Q。因此，在整個量程內，需要找到一個補償系數，只對有上升沿、下降沿對的脈沖進行補償即可。

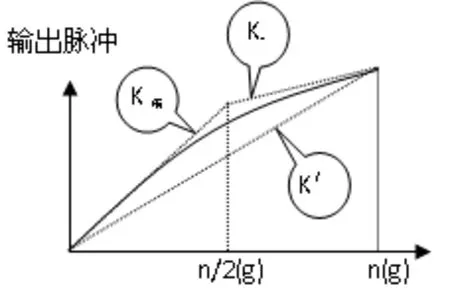
圖6 算法補償前和補償后的斜率示意圖Fig.6 Slope schematic before and after compensation

通過實際測試，可以得到如下初始參數：I/F變換電路中充放電的開關次數M、補償前實際輸出脈沖數N（輸出脈沖數是由輸出脈沖波與頻標相與之后得到的脈沖數），得到補償后接近理想狀態的輸出脈沖數N理為：

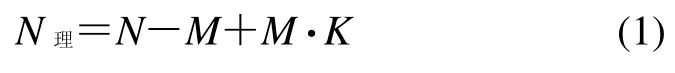
式中的K即為補償系數。經過分析推理、計算及反復測試，最終得到了I/F變換電路的線性度補償公式：

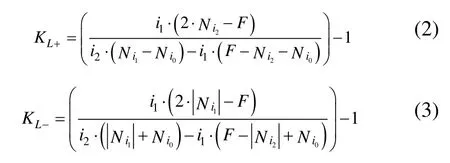
式中，KL+為正向通道的補償系數；KL-為負向通道的補償系數；i1為補償前，輸入電流1（經測算，一般取量程I0的約1/6）；i2為補償前，輸入電流2（經測算，一般取接近量程I0的一個電流值）；Ni1為輸入電流i1時對應的脈沖數(每秒)；Ni2為輸入電流i2時對應的脈沖數(每秒)；Ni0為輸入電流0時對應的脈沖數(每秒)；F為頻標頻率。

3 測試結果

利用慣組后級數據處理電路實現了軟件數字補償算法及驗證，驗證測試的I/F變換板頻標頻率128 kHz、電流量程約26 mA，補償前、后的30 s累積脈沖數及線性度計算結果如表1 ~表3所示，其中，表1為正向通道補償前、補償后的輸出脈沖數，表2為負向通道補償前、補償后的輸出脈沖數，表3為線性度計算結果，圖7為正向通道補償前、補償后的脈沖輸出曲線，圖8為負向通道補償前、補償后的脈沖輸出曲線。

圖7 正通道補前、補后均折算到1 mA/30 s的脈沖數對比曲線Fig.7 Comparison of pulse curve converted to 1 mA/30 s of positive channel before and after compensation

圖8 負通道補前、補后均折算到1 mA/30 s的脈沖數對比曲線Fig.8 Comparison of pulse curve converted to 1 mA/30 s of negative channel before and after compensation

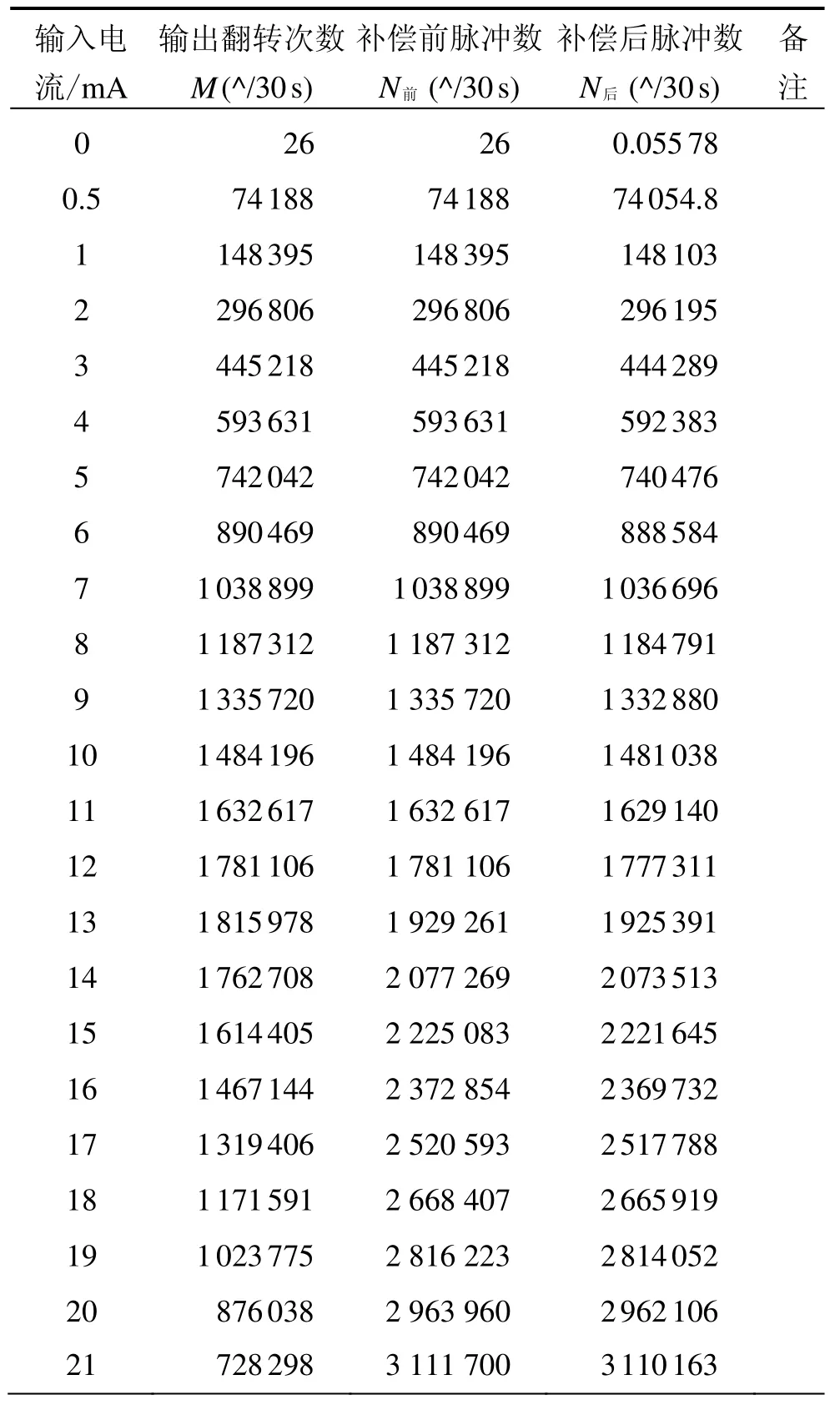
表1 正向通道補償前、補償后的輸出脈沖數Tab.1 Output pulse number of positive channel before and after compensation

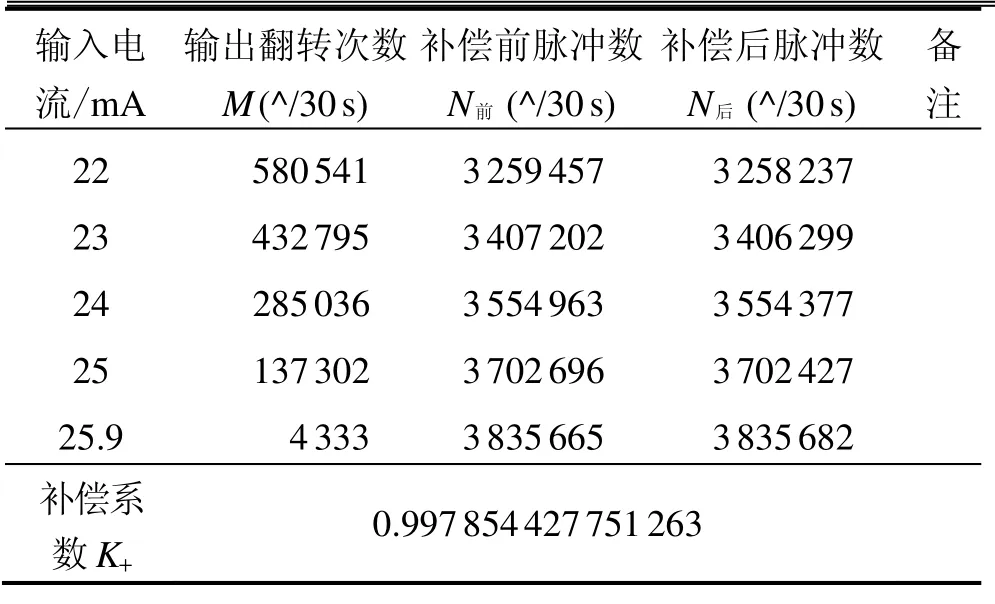
輸入電 輸出翻轉次數補償前脈沖數補償后脈沖數 備流/mAM (^/30 s)N前 (^/30 s)N后 (^/30 s)注22 580 541 3 259 457 3 258 237 23 432 795 3 407 202 3 406 299 24 285 036 3 554 963 3 554 377 25 137 302 3 702 696 3 702 427 25.9 4 333 3 835 665 3 835 682補償系0.997 854 427 751 263數K+

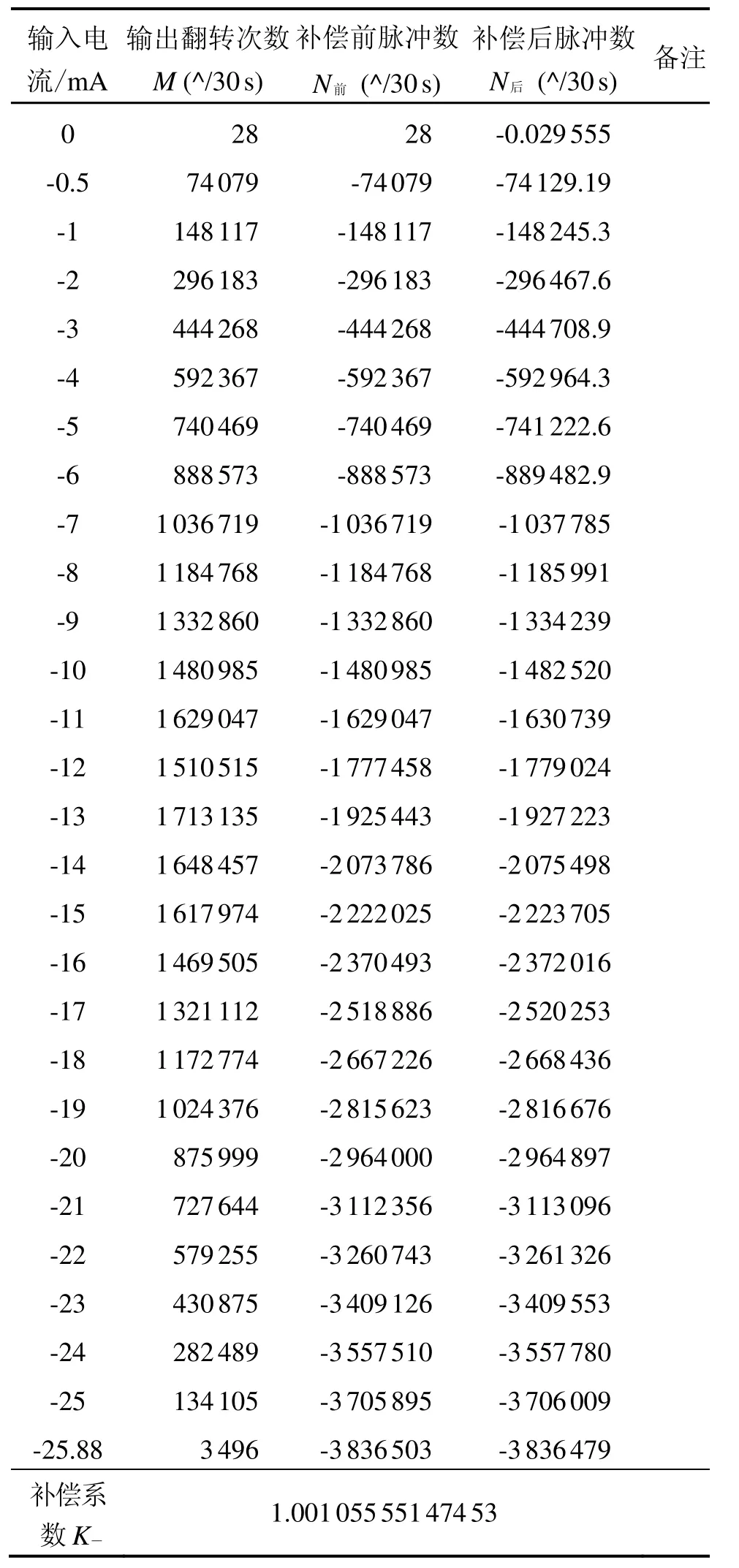
表2 負向通道補償前、補償后的輸出脈沖Tab.2 Output pulse number of negative channel before and after compensation

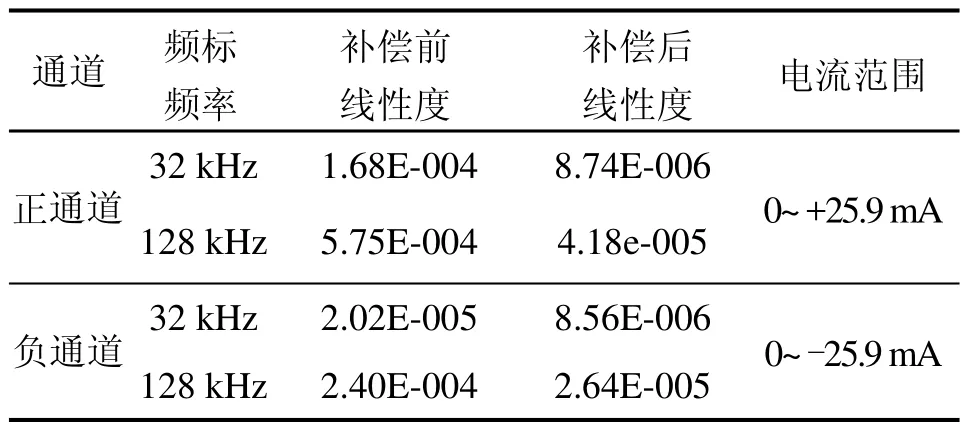
表3 補償前、補償后的線性度Tab.3 Linearity before and after compensation

4 結 論

本文通過理論分析及測試驗證，提出了一種加速度計 I/F變換電路新型數字補償算法，在不改變現有I/F變換板硬件電路的情況下，利用軟件進行數字算法補償，可以將 I/F變換電路的輸出線性度提高一個數量級，特別是在繼續提高電路頻標頻率后，優勢更為明顯。用這種數字補償算法，不僅提高了加速度計通道的靜態精度，同時也提高了動態精度。

此外，該算法在慣導產品中較易實現，結合對稱性補償公式后，I/F變換電路板在生產中完全不需要繁瑣的硬件調試過程，大大簡化了產品的調試工作量，具有較高的實用價值。

（References）：

[1] Azcona C, Calvo B, Celma S, et al. Ratiometric voltageto-frequency converter for long-life autonomous portable equipment[J]. IEEE Sensor Journal, 2013, 13(6): 2382-2390.

[2] 宋雪杰，王曉東，韓軍海. 電流/頻率轉換類型綜述[J].導航與控制，2009，8(1)：31-38.

SONG Xue-jie, WANG Xiao-dong, HAN Jun-hai. The analysis of the type of the current/frequency converter[J]. Navigation and Control, 2009, 8(1): 31-38.

[3] 宋雪杰，趙毅，王曉東. 石英撓性加速度計I/F轉換電路軟件補償研究[J]. 導航與控制，2010，9(2)：52-55.

SONG Xue-jie, ZHAO Yi, WANG Xiao-dong. The compensation research of current-frequency converter of quartz[J]. Navigation and Control, 2010, 9(2): 52-55.

[4] Zhao Tong, Jiang Jianwei. The nonlinear compensation of output frequency of the I/F converter[C]//Mechanic Automation and Control Engineering, 2011: 1782-1785.

[5] Wu Qisong, Yang Haigang, Yin Tao, et al. A high precision CMOS weak current readout circuit[J]. Journal of Semiconductors, 2009, 30(7): 075011 1-6.

[6] 苗新法，王秀華，張明柱，吳榮斌. 閉環加速度計的控制數字化分析[J]. 中國慣性技術學報，2014，22(2)：242-247.

MIAO Xin-fa, WANG Xiu-hua, ZHANG Ming-zhu, WU Rong-bin. Analysis of digital controller for closed-loop accelerometer[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 242-247.

[7] Curey R, Ash M E, Havlicsek H, et al, IEEE Recommended practice for precision centrifuge testing of linear accelerometers[EB/OL] .[2011-09-03]. http://standars .ieee.org/findstds/standard/836-2009.html.

Digital compensation for I/F converter of accelerometer

HUANG Li-juan, SHAO Zhi-hao, ZHENG Yong-qiang, LI Li
(Designing Institute of Hubei Space Technology Academy, Wuhan 430040, China)

The resolution and linearity of quartz flexible accelerometer’s I/F converter are contradictory. Nowadays, this problem prevents the improvement of I/F converter of inertial measurement unit(IMU). By analyzing the existing I/F converter, including the circuitry, the main reasons that affect the output resolution and linearity, and the parameter characteristics of electronic components, a new digital compensation method is put forward. It applies software to realize the linearity’s compensation without changing any hardware, and the compensation formula and parameter calculation are given. The experiments show that the linearity of I/F converter circuit can be improved by an order of magnitude. This method resolves the contradictory of resolution and linearity, simplifies the process of hardware debug, and is easy to implement.

INS; quartz flexible accelerometer; I/F converter; linearity; digital compensation

黃麗娟（1971—），女，高級工程師，從事飛行器慣導產品的設計與研究。E-mail：huanglijuan_825@163.com

1005-6734(2014)04-0547-05

10.13695/j.cnki.12-1222/o3.2014.04.023

TJ765.4

A

2014-03-28；

2014-07-04

國防863項目（2006AA702106）