基于克里格重構的區域地磁變化場短時預測模型

牛 超，劉代志，王躍鋼，李夕海，楊曉君

（第二炮兵工程大學，西安 710025）

基于克里格重構的區域地磁變化場短時預測模型

牛 超，劉代志，王躍鋼，李夕海，楊曉君

（第二炮兵工程大學，西安 710025）

區域地磁變化場建模與預測是地磁輔助導航、空間環境監測與預報等領域的重要研究課題。結合時域上的單臺站地磁變化場預測，以及空間域上的區域地磁變化場重構，提出了一種基于克里格重構的區域地磁變化場短時預測模型。以區域范圍（101°E~111°E，30°N~40°N）的地磁測站2009年的數據為實例，結果表明：1）基于克里格方法重構的區域地磁變化場 Z分量，準確合理的反映了其時空變化特性；2）在短時預測中，區域模型能緊跟地磁變化場的變化趨勢，說明其能很好地描述變化磁場的時空演化特性，且位于區域邊緣的臺站預測誤差稍大。當預測期為1 h、6 h、12 h、24 h時，區域地磁變化場預測模型的平均絕對誤差分別為1.67 nT、2.19 nT、2.72 nT、3.14 nT。

克里格重構；區域地磁變化場；預測模型；地磁導航

地磁導航是利用地球穩定磁場（包括主磁場和局部磁異常場）進行匹配制導的一種新型導航方法[1-2]。變化磁場雖然只占地球總磁場的 1%左右，但是對地磁導航的影響巨大，一般來說，其日變幅高達幾十納特[3]。文獻[4]亦指出在我國某區域，地磁分量值每千米的最大變化量也不過3.6 nT。而目前普通的地磁匹配基準圖只能反映地球穩定磁場，無法對地球變化磁場做出自適應的修正。因此，區域地磁變化場的分析和建模研究很重要，并且其在應用地磁學研究的許多領域都有作用體現，如高精度陸地、海洋磁力測量中的日變改正；震磁效應研究等。

變化磁場建模不同于穩定磁場。穩定磁場中的地殼磁異常場其空間分布復雜但時間演化上較穩定。小至一塊磁性巖石，大至整個地殼，都有其特有的磁場分布，因此，要建立穩定磁場模型，需要大量的空間采樣點。而地球變化磁場雖然也具有復雜的空間分布與時間演化，但其規律性也較明顯，一個地磁觀測站能夠以一定精度表達一片區域的變化磁場，如果利用區域內多個地磁測站，則能以更高精度表達較大區域的變化磁場，循此規律性利用現代智能信號處理方法輔以地統計學理論，就可對其做出較高精度的預測。因此，本文結合時域上的單臺站地磁變化場預測，以及空間域上的區域地磁變化場克里格重構，提出了一種基于克里格重構的區域地磁變化場預測模型。

1 基于改進克里格法的區域地磁變化場重構及精度評估

1.1 區域地磁變化場的克里格重構理論

克里格法是由Krige提出的一種地統計學方法。已有學者基于克里格法進行了電離層相關參數（如電離層TEC、f0F2）的區域重構問題研究[5-8]，并取得了較好的效果。

將克里格法用于地磁變化場區域重構，設 B(x,y)為地磁變化場的某個地磁分量，已知區域內n個地磁臺站的地磁變化場某地磁分量值 B(xi,xj)，其中 i= 1,2,…, n，則區域內任一點 (x0,y0)的克里格估計量 Bp(x0,y0)可表示為：

式中， Wi為權重系數。Benkova[9]指出，在一定空間范圍內，地磁變化場的差異性在經度和緯度方向上是不同的，緯度效應較經度效應更大些，兩者大概差一個量級。因此，這里對算法中的空間距離進行了改進，以將克里格法用于地磁變化場區域重構。對于空間兩點 Pi和 Pj，引入地磁變化場距離d，則 Pi和 Pj的之間距離 dij定義為：

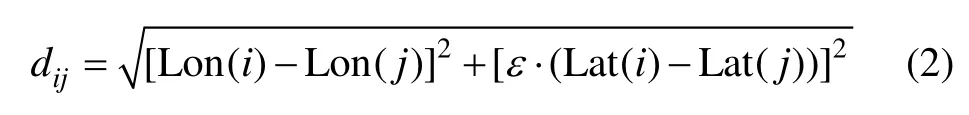
式中，Lon(i)和Lat(i)分別為i點的經度和緯度；ε為尺度因子，以考慮地磁變化場隨空間的分布在經向和緯向的區別，這里選取 ε= 10。

變異函數采用通過原點的線性型：

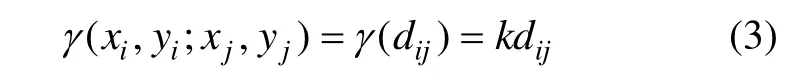
可得到用于地磁變化場區域重構的克里格方程組：

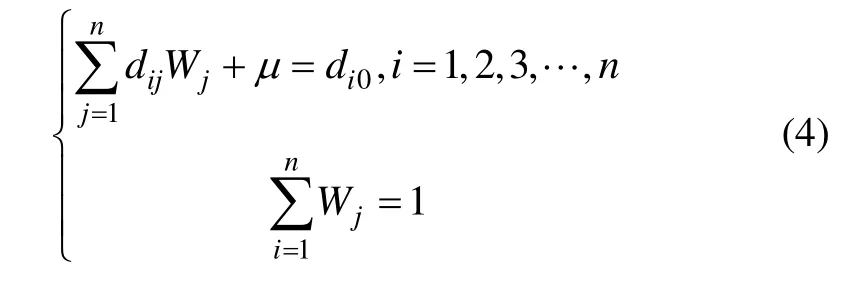
該方程組與變異函數的斜率無關，及線性模型的斜率并不影響重構的結果。

1.2 重構精度評估

地磁變化場的重構精度用交叉驗證法（Cross validation）來衡量。計算重構值 ZEstimation和實測值ZMeasure之差的均方根值σ(稱為重構誤差)，并作為評估重構方法優劣的標準：

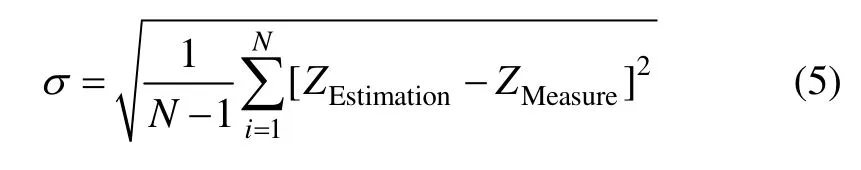
式中，N為參加評估的樣本數。

2 區域地磁變化場重構實例

2.1 數據基礎

我國有著分布合理的國家地磁臺網和區域地磁測陣。這些地磁臺站能夠提供比較準確的地磁分量值，對于區域地磁變化場的分析與建模有很大幫助。圖 1為所選區域（101°E～111°E，30°N～40°N）的地磁測站位置示意圖。

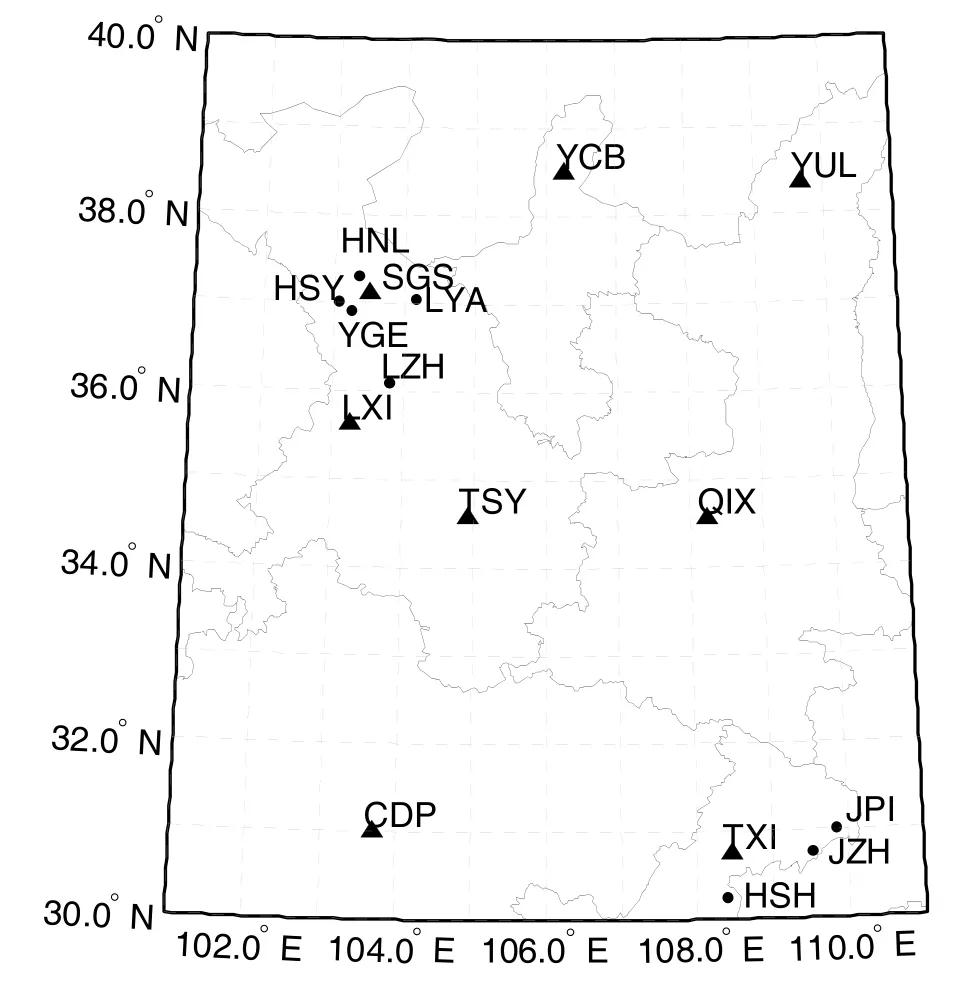
圖1 區域地磁測站的位置示意圖Fig.1 Location map of the geomagnetic observatory in regional area

由于Z分量是地磁輔助導航中地磁場建模與預測的優良匹配分量[10]，因此，本文選擇地磁場Z分量進行區域重構及建模分析。

2.2 重構實例

在該區域內，選取了8個地磁臺站（榆林YUL、天水TSY、乾陵QIX、銀川YCB、天星TXI、臨夏LXI、松山SGS、成都CDP，臺站位置見圖1中三角形所示）的2009年實測數據，基于改進克里格法，進行區域地磁變化場重構。

地磁變化場Z分量在時間上的演化規律主要隨地方時變化。午夜時段（0200LT）曲線較為平緩，在太陽升起前一段時間（一般到0800LT），地磁Z分量逐漸增大，此后，隨后隨著太陽高度角的逐漸增大，地磁Z分量逐漸減小，一直到正午（1200LT左右），此時，地磁Z分量達到最低點，之后地磁Z分量開始逐漸增大，一直到日落（2000LT），地磁Z分量趨于平緩。如圖2所示。

因此，這里選取了四個典型時刻（0800LT（日出）、1200LT（午后）、2000LT（日落）、0200LT（午夜））進行地磁Z分量的重構。圖3給出了該區域2009年8月18日0800LT（日出）、1200LT（正午）、2000LT（日落）、2009年8月19日0200LT（午夜）的四幅實測地磁變化場Z分量重構圖。根據該區域內8個地磁臺站實測地磁變化場Z分量值，以30＇×30＇為網格，重構了該區域的地磁變化場Z分量等值線圖。圖中三角形代表地磁臺站位置，臨近的數字代表相應時刻的實測地磁變化場Z分量值，等值線上的數字代表等值線對應的值。

圖 3(a)為 2009.8. 18日出（0800LT）的重構圖像，由于太陽從東方升起，所以從圖 3(a)可以看出等值線上的數值從東向西遞增，東西向梯度較顯著；圖3(b)為2009. 8.18正午（1200LT）的重構圖像，由于太陽高度角比較大，地磁變化場Z分量絕對值整體較大，且等值線從北向南逐漸增大，梯度變化也較大，在 25°N 附近達到最大值，這反映了它正處于北半球Sq電流渦焦點處；圖3(c)(d)分別為2009.8.18日落（2000LT）和2009.8.19午夜（0200LT）的重構圖像，此時已處于夜晚，所以等值線數值較小。可見，用Kriging方法重構區域范圍的地磁變化場Z分量，以三維的形式（時間，緯度，經度）展示了地磁變化場Z分量的變化，合理的反映了其時空變化特性，所以可以預期把該方法應用于區域地磁變化場Z分量的現報和預報中。

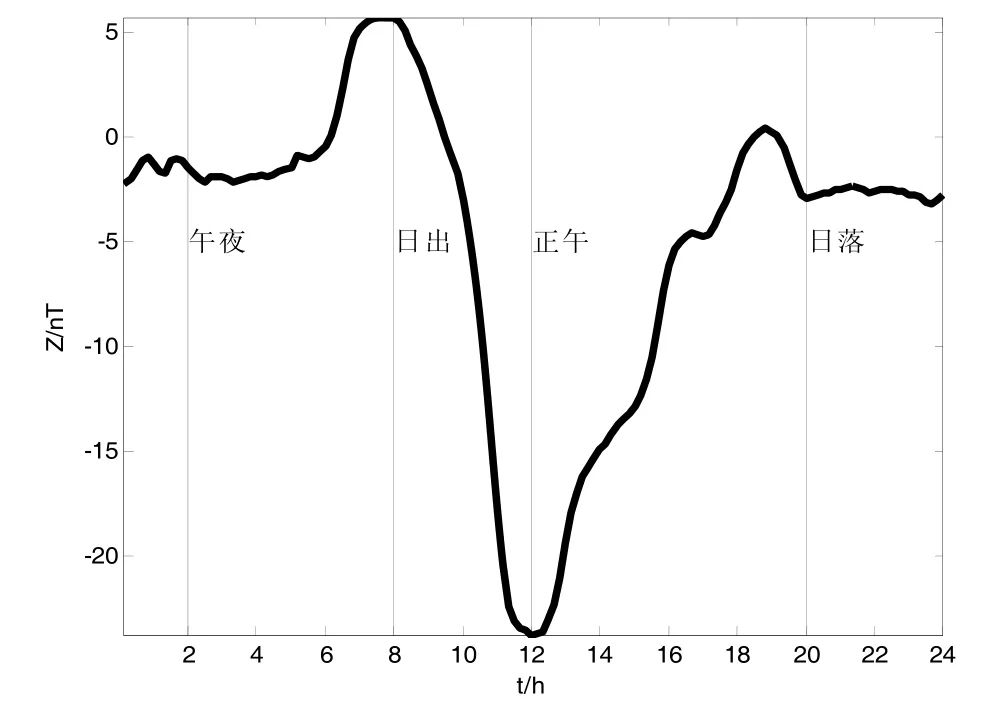
圖2 地磁變化場Z分量日變化曲線（成都臺站2009.8.13LT0000:2400）Fig. 2 Diurnal curve of geomagnetic Z component (CDP observatory 2009.8.13LT0000:2400)

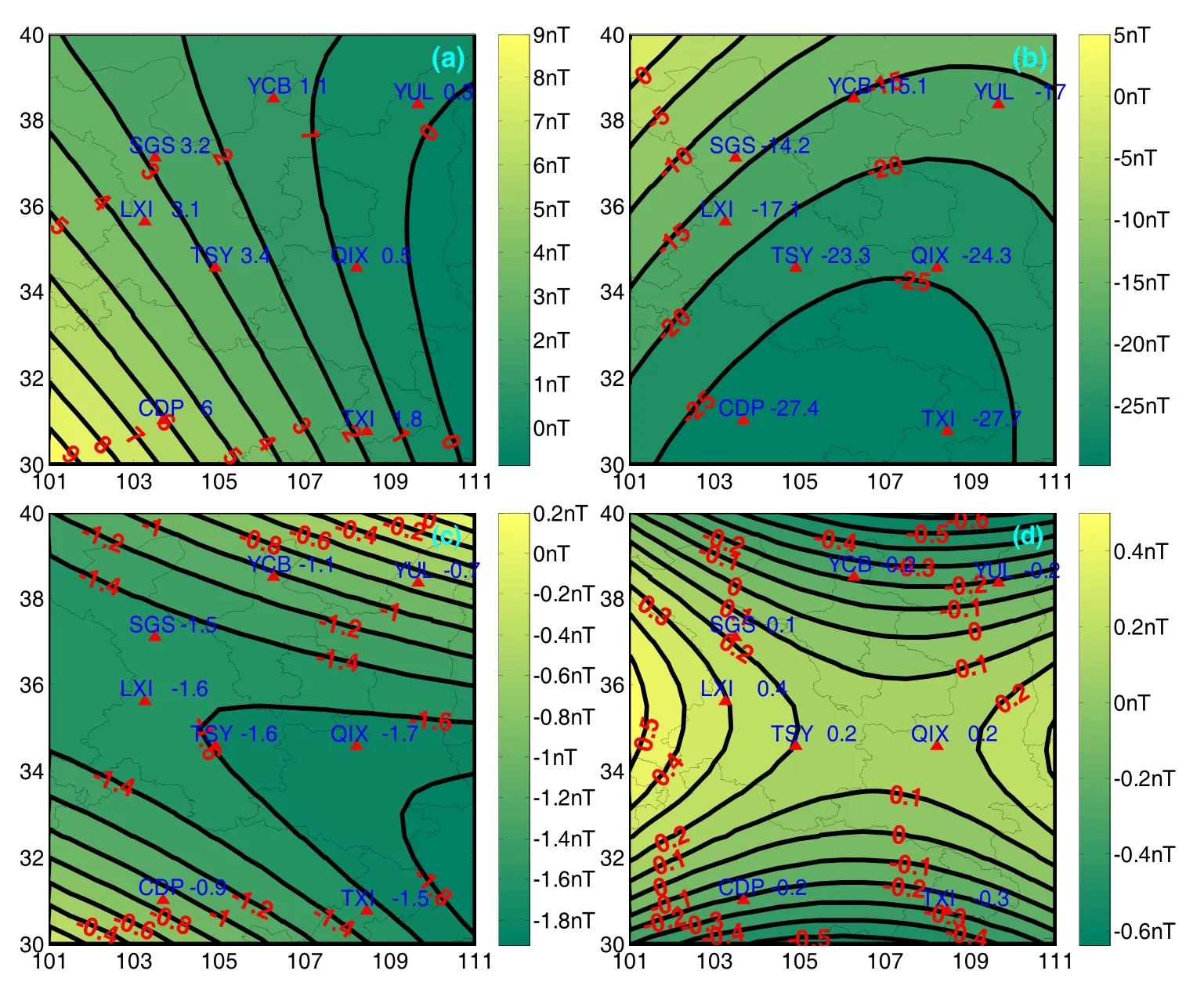
圖3 地磁變化場Z分量四個典型時刻重構等值線分布圖：(a) 0800LT日出；(b) 1200LT正午；(c) 2000LT日落；(d) 0200LT午夜Fig. 3 Reconstruction contour maps of geomagnetic Z component at four typical time: (a) 0800LT Sunrise; (b) 1200LT Noon; (c) 2000LT Sunset; (d) 0200LT Midnight

2.3 重構誤差分析

為了評估地磁變化場Z分量重構的準確性和合理性，對其重構誤差進行了統計。因地磁變化場具有明顯的勞埃德（Lloyd）季節變化，3、4、9、10月為分點月份，用E表示，5、6、7、8月為夏至點月份，用J表示，11、12、1、2月為冬至點月份，用D表示，且每天的地磁活動情況均不同，所以為了更全面地說明地磁變化場Z分量的區域重構效果，表1~3分別給出了該區域2009年8月份四個典型時刻、2009年三個不同勞埃德月份，以及不同地磁活動水平的平均重構誤差結果。

對結果進行分析發現：地磁場本身的變化、地磁活動水平和臺站布局是區域重構誤差的主要來源。對于第一個因素，根據地磁變化場的日變特性，午夜Z分量的數值較小，且變化比較穩定，因此重構誤差較小，而在正午時，磁層——電離層電流體系強度較大，Z分量絕對值較大，此時的重構誤差就大些，這由表1結果可以直觀看出。對于第二個因素，不同的地磁活動水平影響著區域地磁變化場的重構精度，從長時間范圍看，主要體現在不同的勞埃德季節方面，地磁夏至點月份（J）誤差較大，其次為地磁分點月份（E），地磁冬至點月份誤差最小（D），其根源為日地距離不同引起的輻射不同，這由表2可以直觀看出。從短時間范圍來看，重構誤差正比于地磁活動水平，地磁活動較劇烈時，重構誤差較大，比如發生大的地磁擾動，甚至磁暴，從表3可以直觀看出。對于第三個因素，從表1-3均可以看出，若一個臺站其周圍有多個臺站，且形成包圍布局，比如天水TSY和乾陵QIX，該臺站的重構誤差就比較小；反之，若臺站處于區域邊緣，則誤差較大。

表1 區域地磁變化場Z分量重構誤差（2009年8月四個典型時刻）Tab.1 Reconstruction error of regional geomagnetic Z component (four typical times in 2009.8) unit: nT

表2 區域地磁變化場Z分量平均重構誤差（不同勞埃德季節）Tab.2 Reconstruction error of regional geomagnetic Z component (different geomagnetic Lloyd seasons) unit: nT

表3 區域地磁變化場Z分量平均重構誤差（不同地磁活動水平）Tab.3 Reconstruction error of regional geomagnetic Z component (different geomagnetic activity levels) unit: nT

3 基于克里格重構的區域地磁變化場預測模型

3.1 建模步驟

前期已做了單站地磁變化場的 MEEMD-樣本熵-LSSVM預測模型相關研究，這里將時域上的單站地磁變化場Z分量預測，和地域上的區域地磁變化場重構相結合，以進行區域地磁變化場的短時預測。利用地磁臺站的實測地磁變化場數據，給出區域范圍的預測等值線，并對該方法的預測精度進行評估。

預測任務：區域范圍內任一地點地磁變化場的短時預測值（提前1~24 h預測）。

具體步驟：

1）數據處理：將區域內所有地磁臺站的變化磁場Z分量序列最小時間尺度劃歸到10 min，形成各臺站10 min均值的地磁變化場Z分量序列；

2）單站預測：對區域內的每個地磁臺站，采用MEEMD-樣本熵-LSSVM預測模型，預測各個站提前1~24 h的地磁變化場Z分量值，評估單站預測精度；

3）區域重構及預測：對區域內N個地磁臺站某一時刻的地磁變化場Z分量預測值進行區域重構，即可求得區域內任一地點地磁變化場Z分量預測值，給出提前 1 ~24 h的預測等值線，評估其預測誤差。

3.2 短時預測實例

首先進行單站預測。用2009.8.13LT0800LT至8.18LT0800T共5天的數據做模型訓練，用2009.8.18LT0800至2009.8.19LT0800共1天的數據做模型預測檢驗，分別做提前1 h、6 h、12 h、24 h的單站預測。在此基礎上，對區域內 8個地磁臺站某一時刻的預測值，進行區域重構。圖4(a)(c)(e)(g)分別為提前1 h、6 h、12 h、24 h預測的等值線分布圖，網格為30＇×30＇，圖 4(b)(d)(f)(h)為對應時刻根據實測值重構的等值線分布圖。提前 1 h預測的時刻為2009.8.18LT1200，提前 6 h預測的時刻為2009.8.18LT1400LT，提前12 h預測的時刻為2009.8.18LT2000，提前24 h預測的時刻為2009.8.19LT0800。

從圖4(a)(b)(c)(d)可以看出，根據預測值以及實測值重構的等值線圖，其形狀、大小及尺度很相似，這說明了本文提出的預測方法在提前1 h和6 h預測情況下是可以實施的并達到了一定的精度，預測結果比較準確的反映地磁變化場的時空變化特性，但從圖4(e)(f)(g)(h)可以看出，根據預測值重構的等值線圖與根據實際觀測值重構的等值線圖差異性較大，說明隨著預測時長的增大，預測難度增大。

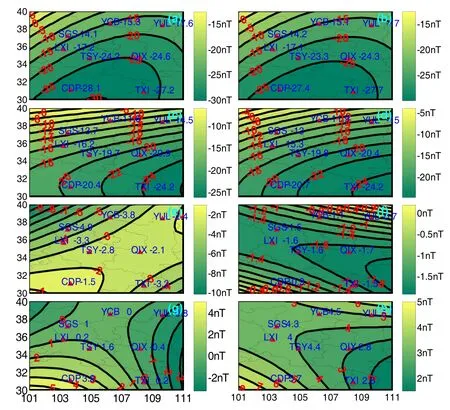
圖4 根據預測值和實測值重構的等值線分布圖，(a)(c)(e)(g)分別為提前預測1 h、6 h、12 h、24 h等值線分布圖，(b)(d)(f)(h)分別為對應時刻的根據實測值重構的等值線分布圖Fig. 4 Reconstruction contour map of forecasting value and observed value, (a)(c)(e)(g) respectively represent the contour map for 1 h, 6 h, 12 h, 24 h ahead predictions, (b)(d)(f) (h) respectively represent the contour map of observed value for the corresponding time

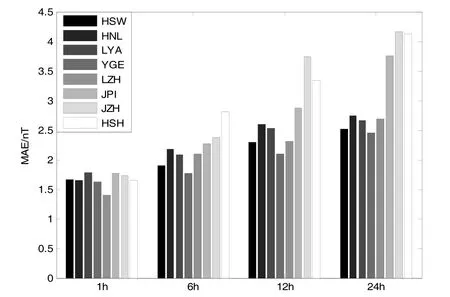
圖5 區域內檢驗臺站預測期分別1 h、6 h、12 h、24 h的平均絕對誤差Fig. 5 Mean absolute errors for forecasting period 1 h, 6 h, 12 h, 24 h of test geomagnetic observatory

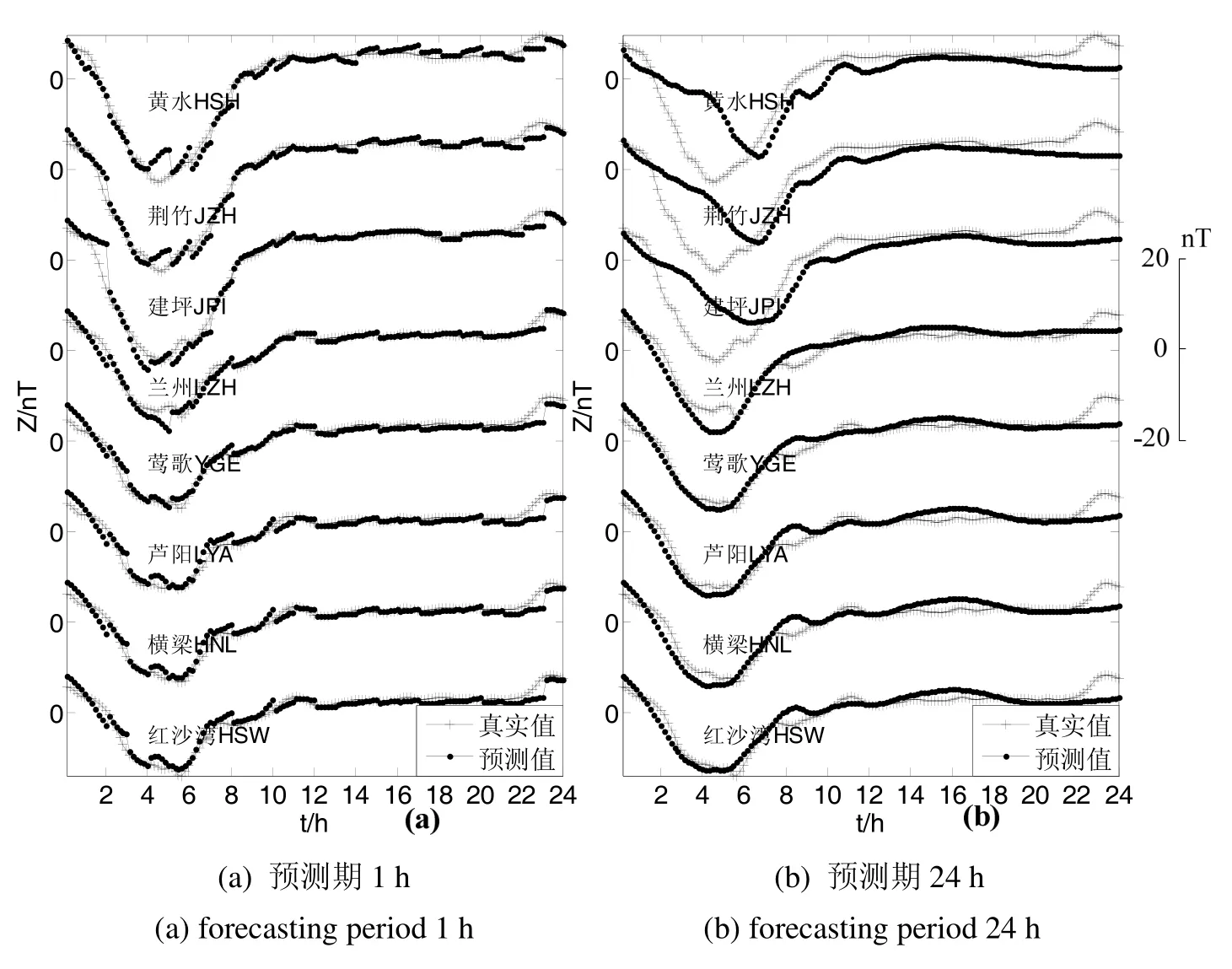
圖6 區域內檢驗臺站預測結果Fig. 6 Forecasting results of test geomagnetic observatory

3.3 區域預測精度評估

基于區域內其它幾個檢驗地磁臺站(圖 1中圓點所示臺站)進行精度評估，采用平均絕對誤差(Mean Absolute Error，MAE)作為預測評價函數。在所選區域內獲取數據的臺站還有：紅沙灣(HSW）、橫梁(HNL)、蘆陽(LYA)、鶯歌(YGE)、蘭州(LZH)、建坪(JPI)、荊竹(JZH)、黃水(HSH)，用這些臺站的數據分別做預測期為1 h、6 h、12 h、24 h的檢驗。圖5為區域內各檢驗臺站預測期為1h、6 h、12 h、24 h的平均絕對誤差。圖6為檢驗臺站預測期分別為1 h、24 h的預測結果示意圖。

4 結 論

本文討論了一種基于克里格重構的區域地磁變化場預測模型，以區域范圍（101°E~111°E，30°N~ 40°N）的地磁測站2009年的數據為實例，結果表明：1）基于克里格方法重構的區域地磁變化場Z分量，準確合理地反映了其時空變化特性；2）在短時預測中，重構預測模型能緊跟地磁變化場的變化趨勢，說明其能很好地描述變化磁場的時空演化特性。本文為實現區域地磁變化場短時高精度預測提供了新的思路，對于更好地推動地磁輔助導航等軍事工程應用有一定的意義。

（References）：

[1] 朱占龍，楊功流，單友東，等. 一種關于地磁圖適配型分析的綜合評價方法[J]. 中國慣性技術學報，2013，21(3)：375-380.

ZHU Zhan-long, YANG Gong-liu, SHAN Youdong, et al. Comprehensive evaluation method of geomagnetic map suitability analysis[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 375-380.

[2] 王仕成，劉元元，孫淵，等. 基于 Legendre函數的超高階地磁場建模方法[J]. 中國慣性技術學報，2012，20(3)：333-338.

WANG Shi-cheng, LIU Yuan-yuan, SUN Yuan, et al. Method for ultra highorder magnetic model based on Legendre function[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 333-338.

[3] 李軍輝，李琪，王行舟，等.中國大陸地磁場Z分量日變幅的時空特征分析[J]. 中國地震，2012，28(1)：42-50.

LI Jun-hui, LI Qi, WANG Xing-zhou, et al. Spatial and temporal variation of geomagnetic vertical daily ranges in Chinese mainland[J]. Earthquake Research in China, 2012, 28(1): 42-50.

[4] 陳勵華，王仕成，孫淵，等. 地磁緩變區域的多維特征量匹配方法[J]. 中國慣性技術學報，2011，19(6)：720-724.

CHEN Li-hua, WANG Shi-cheng, SUN Yuan, et al. Matching of multi-dimensional feature elements in areas with smooth magnetic fields[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 720-724.

[5] Sparks L, Blanch J, Pandya N. Estimating ionospheric delay using kriging: 1. Methodology[J]. Radio Science, 2011, DOI: 10.1029/2011RS004667.

[6] Foster M P, Evans A N. An evaluation of inter- polation techniques for reconstructing ionospheric TEC Maps[J]. Geoscience and Remote Sensing, 2008, 46(7): 2153-2164.

[7] Wang R, Zhou C, Deng Z, et al. Predicting foF2 in the China region using the neural networks improved by the genetic algorithm[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2013, 92: 7-17.

[8] Habarulema J B, Mckinnell L A. Investigating the performance of neural network backpropagation algorithms for TEC estimations using South African GPS data [J]. Ann. Geophys., 2012, 30: 857-866.

[9] Benkova N P. Spherical harmonic analysis of the Sq variations[J]. Terr. Mag. Atomos. Elect, 1940, 45, 425.

[10] 齊瑋，王秀芳，李夕海，等. 基于統計建模的地磁匹配特征量選擇[J]. 地球物理學進展，2010，25(1)：324-330.

QI Wei, WANG Xiu-fang, LI Xi-hai, et al. Selection of characteristic components for geomagnetic matching based on statistical modeling[J]. Progress in Geophysics, 2010, 25(1): 324-330.

Regional geomagnetic short-term forecasting model based on Kriging reconstruction method

NIU Chao, LIU Dai-zhi, WANG Yue-gang, LI Xi-hai, YANG Xiao-jun
(The Second Artillery Engineering University, Xi’an 710025, China)

The modeling and forecasting of regional geomagnetic variation field is an important research topic of geomagnetic navigation and space environment monitoring. Combining the time-domain forecasting of the single geomagnetic observatory and the space-domain reconstruction of the regional geomagnetic variation field, this paper proposes a regional geomagnetic forecasting model based on Kriging reconstruction method. It shows that: 1) the regional geomagnetic Z component reconstructed by Kriging method can reasonably and accurately reflect its spatial-temporal variation characteristics; 2) the regional model can closely keep up with the trend of geomagnetic variation field in short-term forecasting, which indicates that the model can accurately describe the spatial-temporal evolution characteristics. The forecasting errors of geomagnetic observatory located in the area edge are larger. When the forecasting period is 1 h, 6 h, 12 h, 24 h, the mean absolute error of the regional model is 1.67 nT, 2.19 nT, 2.72 nT and 3.14 nT, respectively.

Kriging reconstruction; regional geomagnetic variation field; forecasting model; geomagnetic navigation

牛超 （1986—），男，博士，工程師，從事地磁導航、地磁信息處理等理論與方法研究。E-mail：niuchao0511@163.com

1005-6734(2014)04-0492-06

10.13695/j.cnki.12-1222/o3.2014.04.013

P318.2

A

2014-02-27；

2014-05-30

國家自然科學基金資助項目（41374154，61304240）