方位引出裝置框架誤差分析與修正

關 勁，熊成強，張 群，趙愛武，徐 凱，戚勇剛

（1. 海軍裝備部，北京 100036；2. 天津航海儀器研究所，天津 300131）

方位引出裝置框架誤差分析與修正

關 勁1，熊成強2，張 群2，趙愛武2，徐 凱2，戚勇剛2

（1. 海軍裝備部，北京 100036；2. 天津航海儀器研究所，天津 300131）

炮兵指揮車通過方位引出裝置實現對目標方向和位置的測量。采用兩環結構的方位引出裝置存在著框架誤差，影響對目標位置和方位角的測量精度。通過應用方向余弦矩陣法，研究了框架誤差的產生機理，推導了框架誤差的補償公式。通過數學分析和仿真，驗證了方位引出框架誤差補償的正確性。實驗結果證明：該補償方案能夠對方位引出兩環結構帶來的框架誤差進行實時修正，補償后的精度（PE）≤0.3 mil，滿足戰技指標要求，實現對目標位置和方位角的準確測量。

方位引出裝置；定位定向系統；方向余弦矩陣法；框架誤差

方位引出裝置是炮兵射擊指揮車的重要組成部分。方位引出裝置的作用是在車載定位定向系統所提供的航向角和水平姿態角的基礎上，測量目標在地理坐標系下的航向角和俯仰角，完成目標方位的解算，為偵察車與指揮車提供目標的姿態和位置數據，滿足快速賦予火炮基準射向和連測炮兵陣地戰斗隊形的要求。同時測定目標方位角、高低角和距離，與車載定位定向系統配合可以完成確定目標位置坐標的功能。

基于體積、重量和成本等方面的考慮，方位引出裝置一般采用兩環結構，比經典慣導平臺的三環結構少了一個水平環。方位引出裝置在載體車頂部安裝，在車內全自動操作，而定位定向系統一般安裝在載體車內，與方位引出裝置安裝不在一個基準上，也無法實現機械基準調整，由于結構上的特殊性，導致其測得的方位角和俯仰角不是地理坐標系下的方位角和俯仰角，需要修正框架誤差，進行解析調平。本文分析了框架誤差的產生機理，用方向余弦矩陣法推導了誤差補償公式，可以達到消除誤差的目的。

1 框架誤差的形成

以地理坐標系 XtYtZt作為參考系，載體系XbYbZb相對地理坐標系的位置由三個姿態角確定，即縱搖角P、橫搖角R和航向角H。按照航向角、縱搖角和橫搖角的定義，可按下列順序分三次轉動得到：

則：

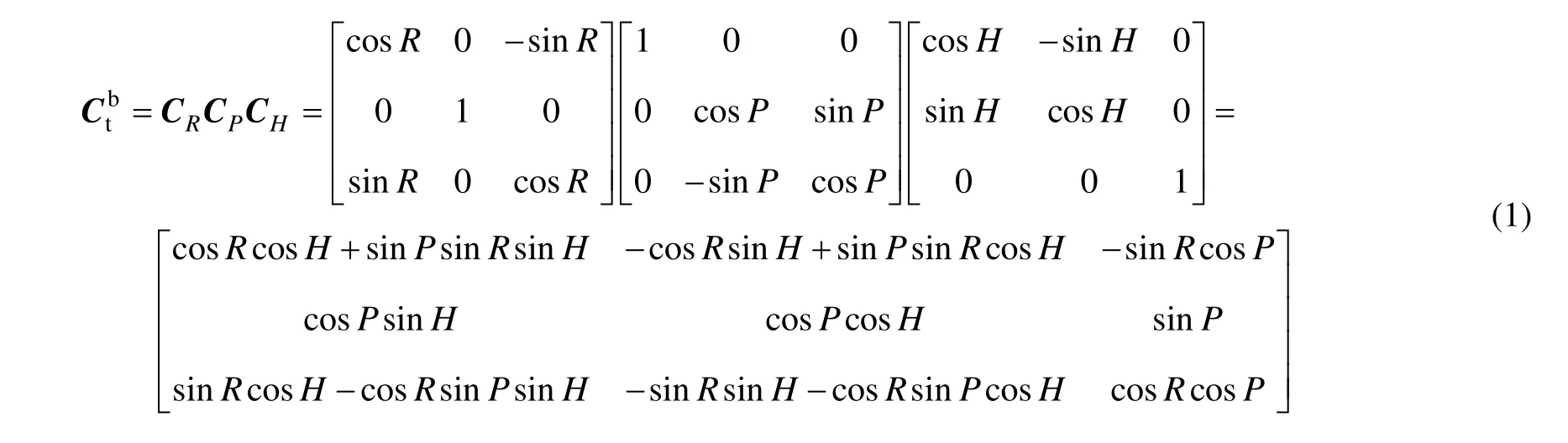
平臺式慣導系統的平臺結構形式如圖1所示。由其結構形式可以得出地理坐標系到載體系的坐標變換矩陣為：

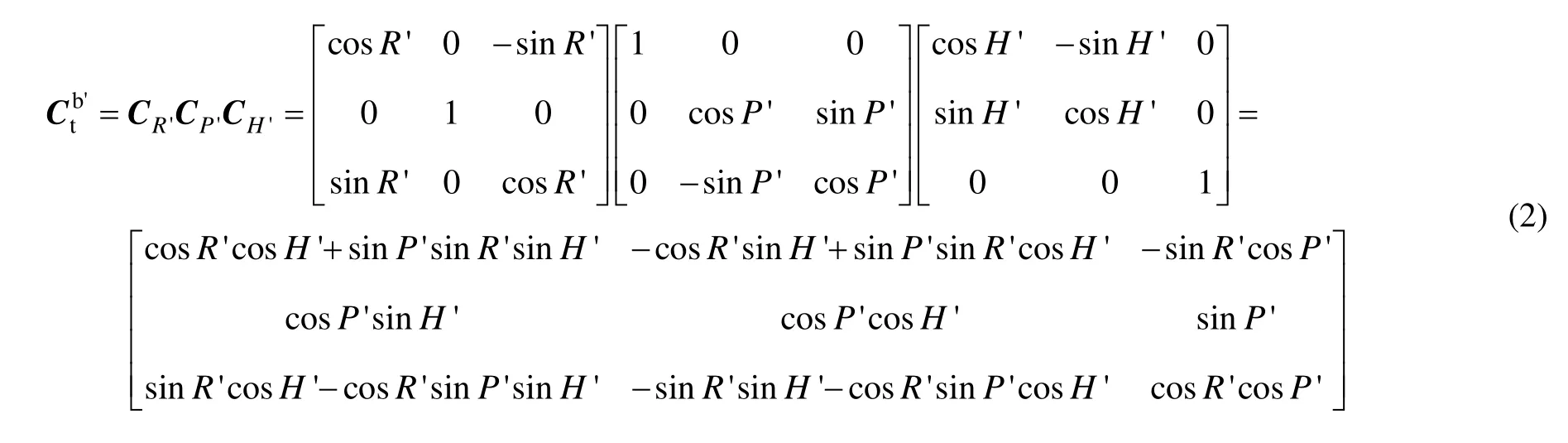
式(2)中， R'、 P'、 H'分別為平臺常平架各環測得的橫搖角、縱搖角和航向角。

比較式(1)和(2)，可以知道，采用這種配置的常平架，其坐標轉換矩陣與標準的平臺系到地理系的變換完全一致，都是先方位，后縱搖，再橫搖的順序，不存在框架誤差。也就是說，在常平架的各個環上測得的姿態角等同于地理系下的標準角度值，不需要進行框架誤差補償，所以圖1所示的平臺結構形式在慣導系統中應用最為普遍。

方位引出裝置由豎軸軸系、水平軸軸系構成雙軸系統，由安裝臺體、方位旋轉支架、底座以及軸承支撐構成框架結構，由角度傳感器、力矩電機、輸電裝置等機電元件構成全自動方位引出裝置的基本組成。方位引出裝置采用了兩環結構，省略了水平橫搖環，如圖2所示。這樣，方位引出裝置上方位環測得的航向角和縱搖環上測得的俯仰角不同于目標在地理坐標系的航向角和俯仰角，需要補償框架誤差，進行修正，才能得到地理坐標系下的方位角和俯仰角，完成位置和姿態解算。

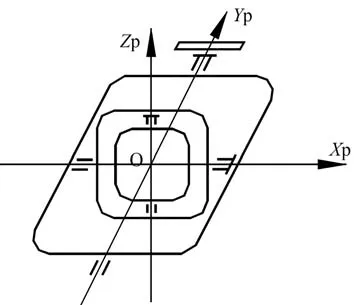
圖1 慣導平臺結構示意圖Fig.1 Structure of inertial platform

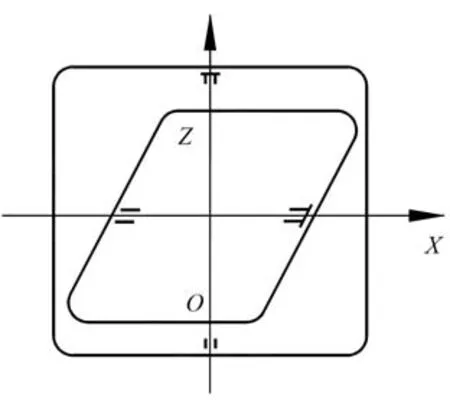
圖2 方位引出裝置結構示意圖Fig.2 Structure of azimuth extractor

2 框架誤差的修正

由框架誤差的產生原因可知，系統的框架誤差是由其結構形式確定的。根據方位引出裝置的結構及其在載車上的安裝方式，可以確定載體系到地理坐標系的矩陣變換要經過五次旋轉：

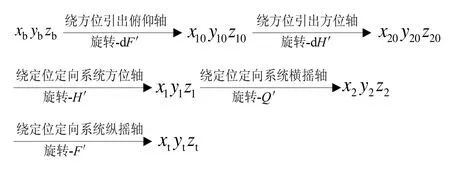
上述過程中，dH′為方位引出測得航向角，dF′為方位引出測得俯仰角，H′、F′、Q′分別為定位定向系統的航向角、縱搖角和橫搖角。

具體變換矩陣如式(3)所示：

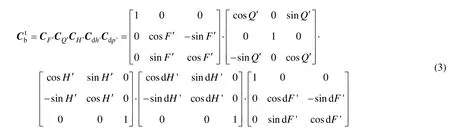
設目標點在地理坐標系內的姿態角為dH、dF、dQ，則變換矩陣應為：

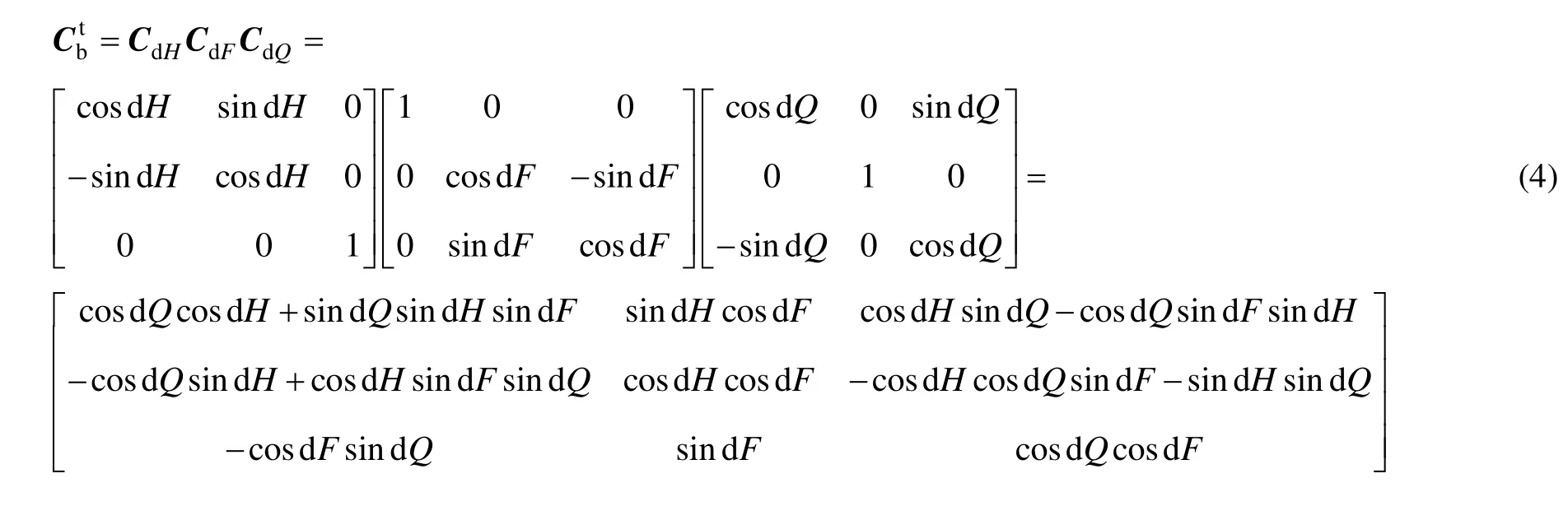
因為目標點在地理坐標系的位置是唯一的，所以這兩個矩陣是相等的。應用三角函數關系，不難得出：

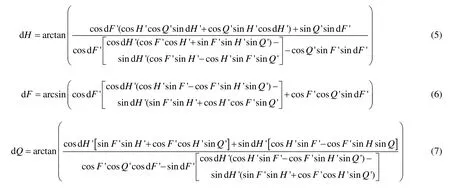
通過上述三個公式，可以由方位引出和定位定向系統的姿態角測量值，得到方位引出所測目標在地理系下的標準姿態角，實現了框架誤差的修正。

3 實驗驗證

以下實驗中，由陀螺經緯儀給定四個標準點A、 B、C、D的航向角值H與高低俯仰角值F，每個標準點經方位引出裝置測量五組值后，運用上述框架誤差修正方法進行解算，最后輸出得出表中實驗值。

經過工作范圍、不同傾斜角狀態下的方位角精度和高低角精度等試驗，多組實驗結果證明精度指標滿足方位角精度(PE)：≤0.3 mil，高低角測量精度(PE)：≤1 mil的戰技指標要求。可見，解析調平的計算是準確的。

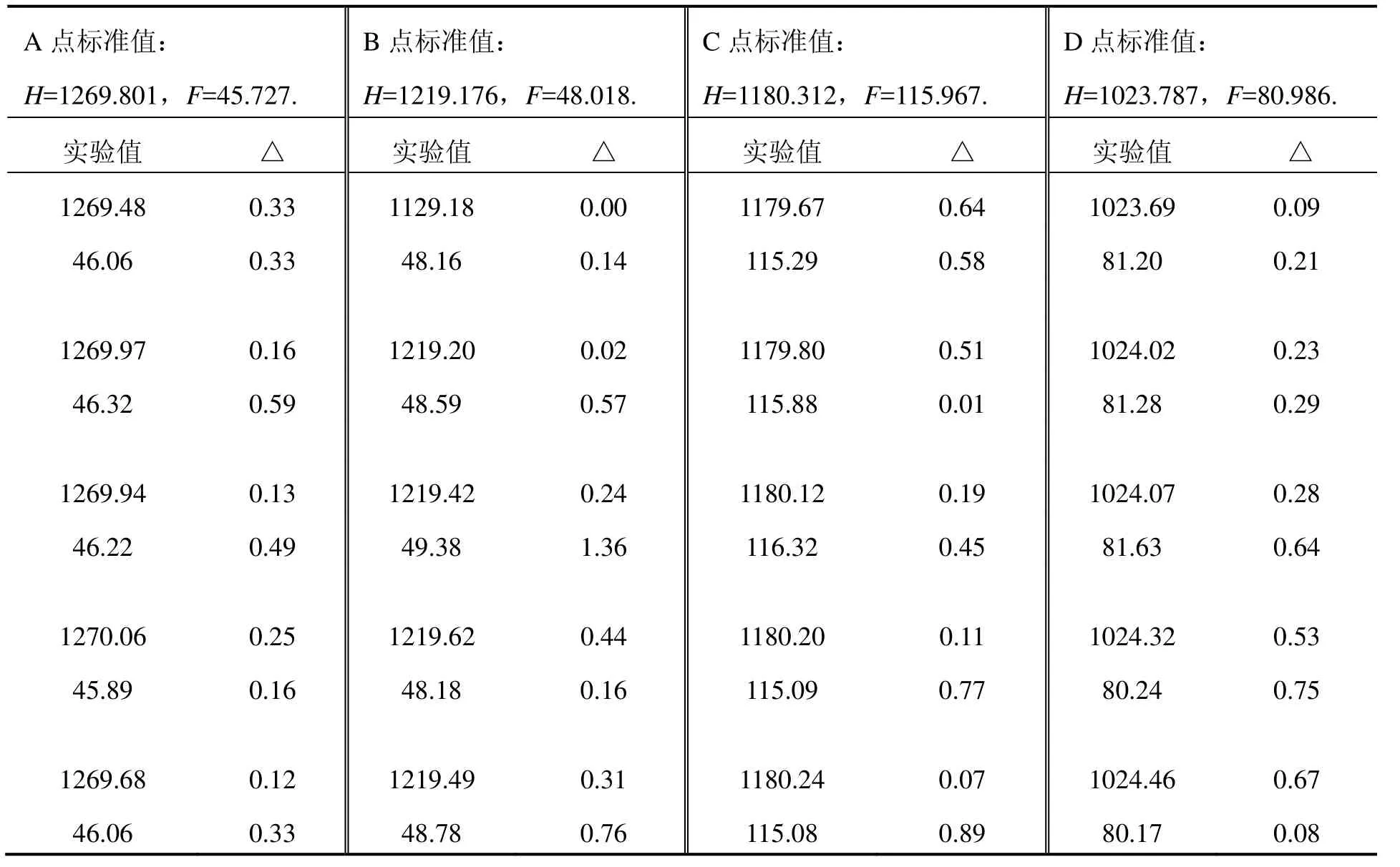
表1 方位角和高低角精度數據Tab.1 Data for precision of azimuth and pitch angle Unit: mil

4 結 論

由于方位引出裝置缺少一個常平架，不能直接由方位引出裝置上航向角和俯仰角來得到目標的位置和方位角。本文對方位引出的框架誤差進行了研究，推導出了方位引出框架補償方案。數學分析和實驗實例表明，該方法計算簡便，準確可靠，實現了框架誤差的補償。

（References）：

[1] 牛立，趙慧. 戰車用慣性定位定向系統的支架誤差分析與補償[J]. 中國慣性技術學報，2007，15(5)：522-525.

NIU Li, ZHAO Hui. Analysis and compensation of the bracket error for inertial positioning and heading system [J]. Journal of Chinese Inertial Technology, 2007, 15(5): 522-525.

[2] Zhang Lei, Wang Anguo. Vessel surface equipment attitude measurement based on conventional inertial reference system[J]. Advanced Material Research, 2012, 629: 878-883.

[3] Titterton D H, Weston J L. Strapdown inertial navigation technology[M]. USA: American Institute of Aeronautics and Astronautics, Inc., 2004: 115-126.

[4] Jordon J W. An accurate strapdown direction cosine algorithms[R]. Report TND-5384, NASA, Washington, 2001.

[5] 胡佩達，高鐘毓，張嶸. 基于三軸搖擺臺的高精度姿態試驗系統[J]. 中國慣性技術學報，2013，21(2)：271-274.

HU Pei-da, GAO Zhong-yu, ZHANG Rong. High accuracy attitude testing system based on three-axis test table[J]. Journal of Chinese Inertial Technology, 2013, 21 (2): 271-274.

[6] Johnson G, Waid J, Primm M, et al. Ship attitude accuracy trade study for aircraft approach and landing operations [C]//IEEE Position Location and Navigation Symposium. 2012: 783-790.

[7] Gu Dongqing, El-Sheimy N, Hassan T, et al. Coarse alignment for marine SINS using gravity in the inertial frame as a reference[C]//IEEE Position, Location and Navigation Symposium. 2008: 961-965.

[8] Yu Q, Jiang G, Fu S, et al. Fold-ray videometrics method for the deformation measurement of nonintervisible large structures[J]. Applied Optics, 2009, 48(24): 4683-4687.

Analysis and correction for gimbal error of azimuth extractor

GUAN Jin1, XIONG Cheng-qiang2, ZHANG Qun2, ZHAO Ai-wu2, XU Kai2, QI Yong-gang2
(1. Equipment Department of the Navy, Beijing 100036, China; 2. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China)

Artillery command vehicle realizes the measurement of the aim’s bearing and position by using a device to extract azimuth. The azimuth extractor with two-ring structure has gimbal error, which would influence the aim’s measurement precision. The generation mechanism of gimbal error was studied and the error’s compensation formula was derived by applying the direction cosine matrix method. The mathematical analysis and simulations verify the correctness of the compensation for the gimbal error of azimuth extractor. The experiment shows that this method could implement real-time correction for the gimbal error, and the precision after compensation is ≤0.3 mil, meeting the requirements for the tactical and technical index and realizing the accurate measurement about the aim’s bearing and position.

azimuth extractor; inertial positioning and heading system; cosine matrix method; gimbal error

關勁（1962—），男，高級工程師，主要從事慣性技術研究和管理工作。E-mail：LJS19672003@163.com

1005-6734(2014)04-0557-04

10.13695/j.cnki.12-1222/o3.2014.04.025

文獻標志碼：

2014-04-14；

2014-07-16

國防科技預研重點項目（51309010101）