玩具中的物理：鑲嵌雪花片的滾動軌跡＊

邱為鋼 陶 濤 俞嘉玲 王妍妍 林超君

（湖州師范學院理學院，浙江 湖州 313000）

有趣的玩具蘊含不少高深的物理，現象看起來非常簡單直觀，但分析起來需要普通物理甚至理論物理的知識.本文研究兩個鑲嵌雪花片在地面上的滾動軌跡.把雪花片（如圖1所示）的側邊涂上顏料，在水平地面上滾動起來，顏料就在地面上留下兩條對稱的軌跡.仔細觀察，這兩條軌跡具有周期性，即某一特征曲線段周期重復.那么這個周期性軌跡是否具有解析表達式，周期長度與哪些幾何（物理）量有關？

圖1

由立體幾何知識可知

由圖2可知OH＝OKsinβ，2OK＝O1K＋O2K.由（1）、（2）兩式計算得到質心縱坐標為

圖2

鑲嵌雪花片的滾動可以分解為質心的平動和饒質心的三維轉動.三維轉動又可以分解為饒3個方向轉動的疊加.取一個在質心的正交坐標系O x y z，第1次繞z軸轉動，轉動后的坐標軸變為O x′y′z′.第2次的轉動方向只能選x′軸方向或y′方向，轉動后的坐標軸變為O x″y″z″，第3次轉動方向不能與第2次重合，所以總的轉軸方向組合只有以下4種：z x′y″，z x′z″，z y′x″，z y′z″.最常用的歐拉轉動對應最后一種，而本文中的轉動對應第3種，這也是處理這個滾動模型的最重要的突破口.起始時刻圓心連線O1O2與地面平行，選為x軸方向，垂直地面向上為z軸方向，與x軸和z軸都垂直的是y軸方向；繞質心O的轉動分解為3個轉動的疊加，第1個轉動是繞z軸轉動φ角度，第2個轉動是繞y′軸轉動-β角度，第3個轉動是繞x″軸轉動-ψ角度.借用歐拉角的名義，稱φ角為進動角，β角為章動角，ψ角為自轉角.設R（n，φ）表示繞n（單位矢量）方向轉動φ角度的轉動矩陣，具體形式為

其中（n1，n2，n3）是單位矢量n的3個分量.設依次轉動后3組正交單位矢量分別為（i，j，k），（i′，j′，k′），（i″，j″，k″），那么滾動后體系上任意一點的坐標為其中（x0，y0，z0）是質心坐標系中任意一點的坐標.

體系滾動后A1、A2與地面接觸，即相對地面坐標的第3分量始終為0，計算得到自轉角ψ滿足的條件為

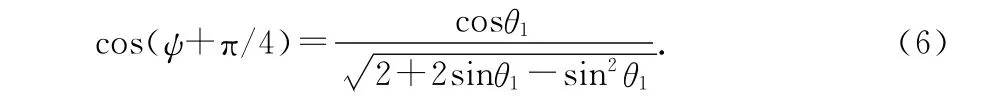
體系做純滾動的必要條件是A1、A2相對地面的速度為0，計算得到進動角φ所滿足的微分方程和質心坐標xc、yc所滿足的微分方程為

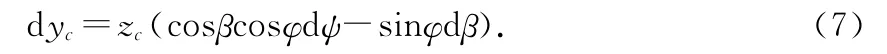
令s＝sinθ1，c＝cosθ1，計算得到進動角φ的表達式為

知道了進動角φ、章動角β、自轉角ψ以及質心坐標（xc，yc，zc）的解析表達式，就能把兩條對稱軌跡的解析表達式求出來.不過，為了表示簡潔、方便與實驗對比，我們取周期軌跡頂點處為坐標原點，以頂點處的切線及其垂線為坐標軸，經過坐標平移和旋轉，在新的坐標軸下兩條軌跡的部分軌跡解析表達式為

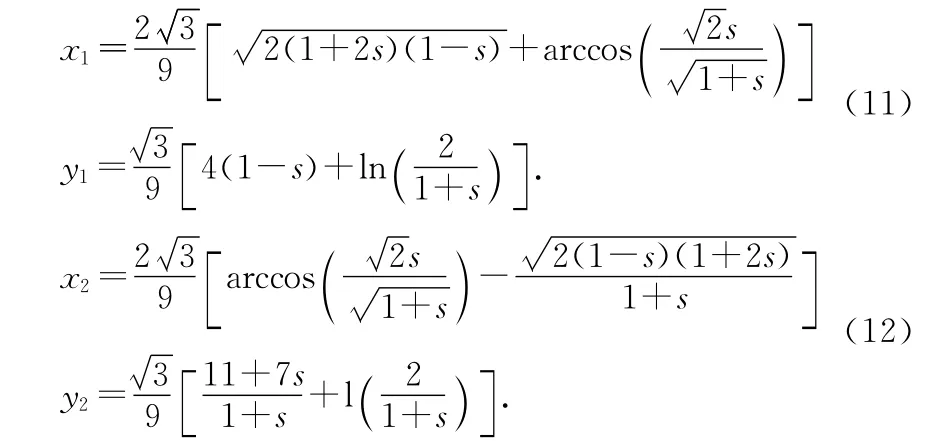
因為雪花片有正反兩面，所以完整的一個周期軌跡的周期長度（兩點距離）是L＝其中R是雪花片（看作圓盤）的半徑.

圖3

這樣，綜合利用中學的立體幾何，大學的轉動矩陣，質心平動加繞質心的轉動，有理分式的不定積分等數學物理知識，得到了鑲嵌雪花片在水平地面做純滾動時，與地面接觸點形成的兩條周期性軌跡的解析表達式，得到了周期長度的解析表達式.這個模型，可以作為玩具中的物理一個經典例子.