二次函數在高考的考點

聶煒藝

二次函數是初中所學的知識，但高中繼續深入學習，在高考中經常涉及，是中學階段的一個重要函數.通常要求學生掌握二次函數的概念、解析式、圖像及性質，能利用二次函數研究一元二次方程的實根分布條件，能求二次函數的區間最值.

一般來說，高考所出的題型包括以下三類：

1.求二次函數的解析式

例1 已知二次函數的對稱軸為x=-2，截x軸上的弦長為4，且過點（0，-1），求函數的解析式.

解 ∵二次函數的對稱軸為x=-2，

設所求函數為f（x）=a（x+2）2+b，

又∵f（x）截x軸上的弦長為4，

∴f（x）過點（-2+2，0）.

f（x）又過點（0，-1），

∴4a+b=0，

2a+b=-1，a=12，

b=-2.

∴f（x）=12（x+2）2-2.

總結：求二次函數的解析式時，要根據條件選擇不同的形式.

2.討論二次函數的區間根的分布

這類問題的情況比較多，在考試時很少單獨出題，數形結合是處理本類題目的重要思想方法.

例2 已知函數f（x）=x2-（2a-1）x+a2-2與非負x軸至少有一個交點，求a的取值范圍.

解法一 由題知關于x的方程x2-（2a-1）x+a2-2=0至少有一個非負實根，設根為x1，x2，

則x1x2≤0或Δ≥0

x1x2>0

x1+x2>0，得-2≤a≤94.

解法二 由題知f（0）≤0或f（0）>0

--（2a-1）2>0

Δ≥0，得

-2≤a≤94.

總結：二次函數的區間根的分布情況一般需從三方面考慮：①判別式;②區間端點的函數值的符號;③對稱軸與區間的相對位置.

3.討論二次函數的區間單調性與最值問題

例3 函數y=x2+bx+c （x∈[0，+∞））是單調函數的充要條件是（ ）.

A.b≥0 B.b≤0 C.b>0 D.b<0

分析 對稱軸x=-b2.

∵函數y=x2+bx+c（x∈[0，+∞）是單調函數，

∴對稱軸x=-b2在區間[0，+∞）的左邊，即-b2≤0，得b≥0.

因此選A.

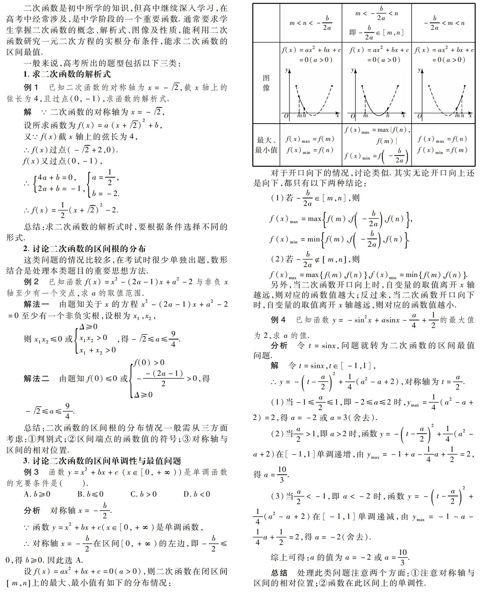
設f（x）=ax2+bx+c=0（a>0），則二次函數在閉區間m，n上的最大、最小值有如下的分布情況：

m

m<-b2a

即-b2a∈[m，n]

-b2a

圖

像f（x）=ax2+bx+c

=0（a>0）

f（x）=ax2+bx+c

=0（a>0）

f（x）=ax2+bx+c

=0（a>0）

最大、

最小值f（x）max=f（m）

f（x）min=f（n）

f（x）max=max{f（n），

f（m）}

f（x）min=f-b2a

f（x）max=f（n）

f（x）min=f（m）

對于開口向下的情況，討論類似.其實無論開口向上還是向下，都只有以下兩種結論：

（1）若-b2a∈[m，n]，則

f（x）max=maxf（m），f-b2a，f（n），

f（x）min=minf（m），f-b2a，f（n）.

（2）若-b2am，n，則

f（x）max=maxf（m），f（n），f（x）min=minf（m），f（n）.

另外，當二次函數開口向上時，自變量的取值離開x軸越遠，則對應的函數值越大;反過來，當二次函數開口向下時，自變量的取值離開x軸越遠，則對應的函數值越小.

例4 已知函數y=-sin2x+asinx-a4+12的最大值為2，求a的值.

分析 令t=sinx，問題就轉為二次函數的區間最值問題.

解 令t=sinx，t∈[-1，1]，

∴y=-t-a22+14（a2-a+2），對稱軸為t=a2.

（1）當-1≤a2≤1，即-2≤a≤2時，ymax=14（a2-a+2）=2，得a=-2或a=3（舍去）.

（2）當a2>1，即a>2時，函數y=-t-a22+14（a2-a+2）在[-1，1]單調遞增，

由ymax=-1+a-14a+12=2，得a=103.

（3）當a2<-1，即a<-2時，函數y=-t-a22+14（a2-a+2）在[-1，1]單調遞減，

由ymax=-1-a-14a+12=2，得a=-2（舍去）.

綜上可得：a的值為a=-2或a=103.

總結 處理此類問題注意兩個方面：①注意對稱軸與區間的相對位置;②函數在此區間上的單調性.