廣義V－r－Ⅰ型不變凸非光滑多目標規劃問題

閆 春 雷

（青島大學 數學科學學院，山東 青島266071）

凸性在數學規劃中應用廣泛.為了減弱對凸性的要求，研究者們給出了幾類廣義凸函數的定義.Hanson［1］介紹了不變凸函數；Hanson等［2］給出了Ⅰ型與Ⅱ型不變凸函數的概念.文獻［3－8］將Ⅰ型不變凸函數推廣到可微或不可微多目標規劃的情形，取得了一些有意義的結果；Jeyakumar等［9］將不變凸的概念推廣到多目標規劃情形，給出了V－不變凸的概念；Antczak［10］結合V－不變凸［9］與r－不變凸［11］給出了V－r－不變凸的概念；Antczak［12］將V－r－不變凸推廣到局部Lipschitz函數，并在局部Lipschitz函數的V－r－不變凸條件下給出了非光滑多目標規劃問題的Karush－Kuhn－Tuker必要與充分最優性條件及Mond－Weir與Wolf型對偶結果；Ahmad等［13］又將V－r－不變凸進行了推廣，給出了局部Lipschitz函數廣義V－r－不變凸的概念，并在廣義V－r－不變凸條件下給出了非光滑多目標規劃問題的Karush－Kuhn－Tuker充分最優性條件及 Mond－Weir對偶性.

本文考慮非光滑多目標規劃問題，結合V－r－不變凸與Ⅰ型不變凸，通過給出局部Lipschitz函數的廣義V－r－Ⅰ型不變凸概念，在廣義V－r－Ⅰ型不變凸條件下得到了非光滑多目標規劃問題的Fritz－John和Karush－Kuhn－Tuker充分最優性條件，并建立了混合型對偶問題，且在廣義V－r－Ⅰ型不變凸條件下給出了弱對偶性與嚴格逆對偶性.

1 預備知識

對于任意的x＝（x1，x2，…，xn）∈?n，y＝（y1，y2，…，yn）∈?n，有x＝y?xi＝yi（i＝1，2，…，n）；x＜y?xi＜yi（i＝1，2，…，n）；x≤y?xi≤yi（i＝1，2，…，n）；x?y?x≤y且x≠y.

定義1［14］設集合X??n非空，f：X→?是實值函數，x∈X，N為x的鄰域，如果存在某個常數K＞0，使得對任意的y，z∈N，有

則稱f在x處是局部Lipschitz的.

若不等式（1）對于任意的x∈X都成立，則稱f在X上是局部Lipschitz的.

定義2［14］X??n為非空開集，函數f：X→?在點x∈X處是局部Lipschitz的，d∈?n.若極限

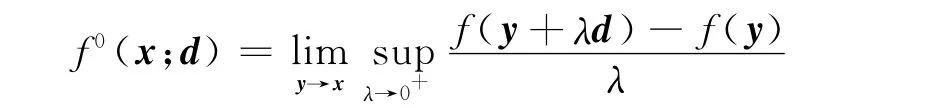
存在，則稱此極限為f在x處沿方向d的廣義方向導數.

定義3［14］X??n為非空開集，函數f：X→?在x∈X的廣義次梯度記為

考慮非光滑多目標規劃問題（VP）：

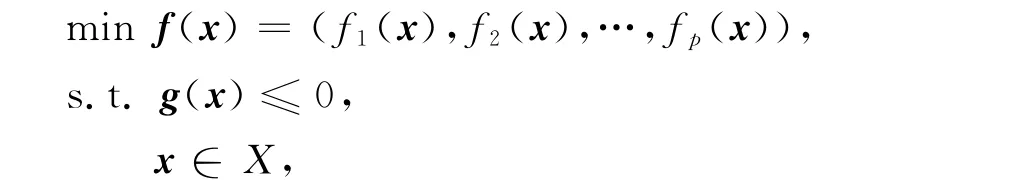
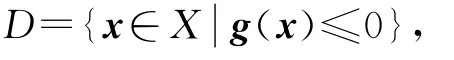
定義5［12］設f：X→?p為定義在非空開集X??n上的局部Lipschitz函數，r為任意實數，如果存在函數η：X×X→?n，αi：X×X→?＋＼｛0｝，i∈I，使得對于任意的x∈X，有

則稱函數f在u∈X處關于η是V－r－不變凸的.若x≠u時，式（2）不等號嚴格成立，則稱函數f在u∈X處關于η是嚴格V－r－不變凸的.

下面假設X為?n中非空開集，f：X→?p，g：X→?m為局部Lipschitz函數.函數η：X×X→?n，αi：X×X→?＋＼｛0｝，βj：X×X→?＋＼｛0｝，νi：X×X→?＋＼｛0｝，ωj：X×X→?＋＼｛0｝，i∈I，j∈M，r為任意實數.

定義6 如果存在函數η及αi，βj（i∈I，j∈M），使得對任意的x∈X，有：

則稱（f，g）在u∈X處關于η 是V－r－Ⅰ型不變凸的.

定義7 如果存在函數η及νi，ωj（i∈I，j∈M），使得對任意的x∈X，有：

則稱（f，g）在u∈X 處關于η 是（偽，擬）V－r－Ⅰ型不變凸的.

若當x≠u時，式（7），（9）中第二個不等號嚴格成立，則稱（f，g）在u∈X處關于η是（嚴偽，擬）V－r－Ⅰ型不變凸的；若當x≠u時，式（8），（10）中第二個不等號嚴格成立，則稱（f，g）在u∈X處關于η是（偽，嚴擬）V－r－Ⅰ型不變凸的.

定義8 如果存在函數η及νi，ωj（i∈I，j∈M），使得對任意的x∈X，有：

則稱（f，g）在u∈X 處關于η 是（擬，偽）V－r－Ⅰ型不變凸的.

若當x≠u時，式（12），（14）中第二個不等號嚴格成立，則稱（f，g）在u∈X處關于η是（擬，嚴偽）V－r－Ⅰ型不變凸的；若當x≠u時，式（11），（13）中第二個不等號嚴格成立，則稱（f，g）在u∈X 處關于η 是（嚴擬，偽）V－r－Ⅰ型不變凸的.

2 最優性條件

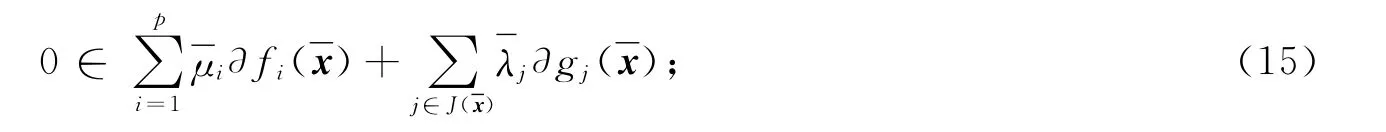
且下列條件之一成立：

由條件1）得

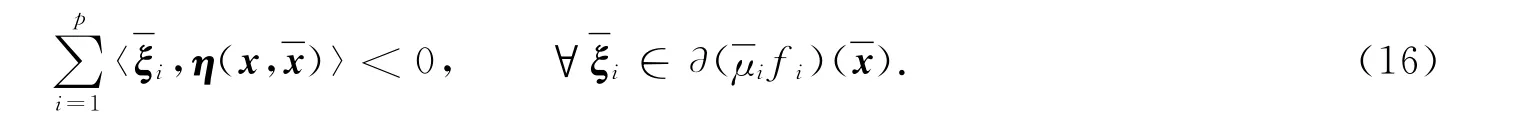
又由條件1）得

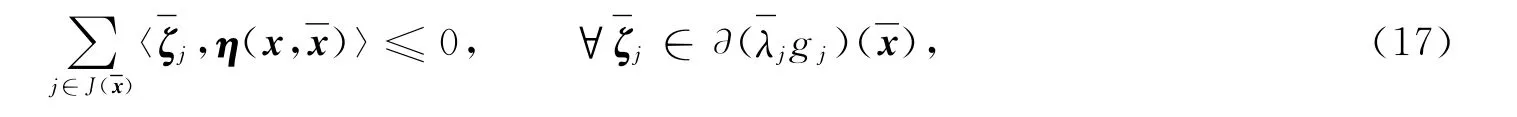
式（16）＋式（17）得

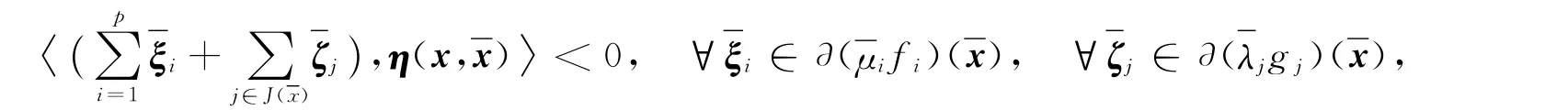
根據次微分的運算性質［14］，得

2）的證明類似1）.由條件2），式（16）中＜0換為≤0，式（17）中≤0換為＜0，仍可得到式（18），結論成立.

由條件1）或條件2）均能得式（16）成立.其余證明與定理1類似.

3 混合型對偶

考慮（VP）的對偶問題（VD）：

定理3（弱對偶）設x，（y，μ，λ）分別為（VP）和（VD）的可行解，如果下列條件之一成立：

又因為

由條件1）及次微分的運算性質［14］，得

因為（y，μ，λ）為（VD）的可行解，有－λjgj（y）≤0，j∈J2.從而

由條件1）及次微分的運算性質［14］，得

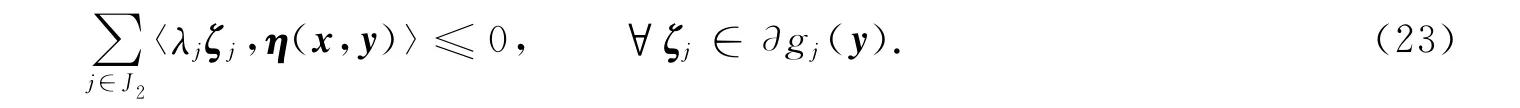
式（21）＋式（23）得

2）的證明類似1）.

定理4（弱對偶）設x，（y，μ，λ）分別為（VP）和（VD）的可行解，如果下列條件之一成立：

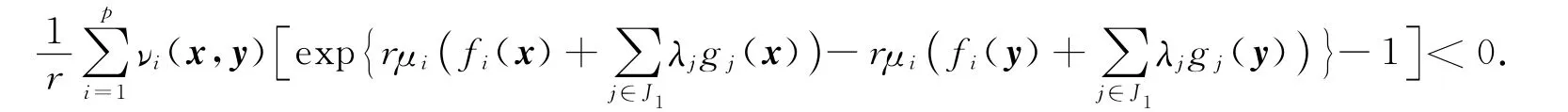
由條件1）及次微分的運算性質［14］知式（21）成立.其余證明與定理3類似.

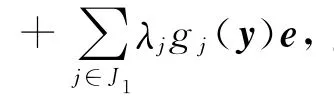
與式（20）矛盾.

2）的證明類似1）.

［1］Hanson M A.On Sufficiency of the Kuhn－Tucker Conditions ［J］.Journal of Mathematical Analysis and Applications，1981，80（2）：545－550.

［2］Hanson M A，Mond B.Necessary and Sufficient Conditions in Constrained Optimization ［J］.Mathematical Programming，1987，37（1）：51－58.

［3］Kaul R N，Suneja S K，Srivastava M K.Optimality Criteria and Duality in Multiple－objective Optimization Involving Generalized Invexity［J］.Journal of Optimization Theory and Applications，1994，80（3）：465－482.

［4］Aghezzaf B，Hachimi M.Generalized Invexity and Duality in Multiobjective Programming Problems［J］.Journal of Global Optimization，2000，18（1）：91－101.

［5］Hanson M A，Pini R，Singh C.Multiobjective Programming under Generalized TypeⅠInvexity［J］.Journal of Mathematical Analysis and Applications，2001，261（2）：562－577.

［6］Mishra S K，Noor M A.Some Nondifferentiale Multiobjective Programming Problems ［J］.Journal of Mathematical Analysis and Applications，2006，316（2）：472－482.

［7］Antczak T.Optimality Conditions and Duality for Nondifferentiale Multiobjective Programming Problems Involving d－r－Type Ⅰ Functions ［J］.Journal of Computational and Applied Mathematics，2009，225（1）：236－250.

［8］Slimani H，Radjef M S.Nondifferentiable Multiobjective Programming under Generalized dⅠ－Invexity ［J］.European Journal of Operational Research，2010，202（1）：32－41.

［9］Jeyakumar V， Mond B.On Generalized Convex Mathematical Programming ［J］.Journal of Australian Mathematical Society：Series B，1992，34（1）：43－53.

［10］Antczak T.V－r－Invexity in Multiobjective Programming［J］.Journal of Applied Analysis，2005，11（1）：63－80.

［11］Antczak T.r－Pre－invexity and r－Invexity in Mathematical Programming ［J］.Computer and Mathematics with Applications，2005，50（4）：551－566.

［12］Antczak T.Optimality and Duality for Nonsmooth Multiobjective Programming Problems with V－r－Invexity ［J］.Journal of Global Optimization，2009，45（2）：319－334.

［13］Ahmad I，Gupta S K，Jayswal A.On Sufficiency and Duality for Nonsmooth Multiobjective Programming Problems Involving Generalized V－r－Invex Functions［J］.Nonlinear Analysis，2011，74（17）：5920－5928.

［14］Clarke F H.Nonsmooth Optimization［M］.New York：Wiley，1983.