E類(lèi)保序嚴(yán)格部分一一變換半群的極大逆子半群

龍偉鋒，游泰杰

（貴州師范大學(xué) 數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，貴陽(yáng)550001）

0 引 言

設(shè)［n］＝｛1，2，…，n｝并賦予自然序，Singn和Pn分別表示［n］上的奇異變換半群和部分變換半群.對(duì)α∈Pn，若對(duì)于任意的x，y∈dom（α），x≤y蘊(yùn)含xα≤yα，則稱(chēng)α為保序部分變換.設(shè)POn為Pn中除恒等變換外所有保序部分變換構(gòu)成的集合，則POn是Pn的子半群［1］，稱(chēng)為保序部分變換半群.記On＝POn∩Singn，則On是POn的子半群［1］，稱(chēng)為（奇異）保序變換半群.令I(lǐng)n表示［n］上的對(duì)稱(chēng)逆半群.設(shè)α∈In，若對(duì)任意的x，y∈dom（α），x≤y蘊(yùn)含xα≤yα，則稱(chēng)α為保序部分一一變換.記POIn為In中除恒等變換外的所有保序部分一一變換構(gòu)成的集合，則POIn是In的一個(gè)逆子半群［2］，稱(chēng)為保序（嚴(yán)格）部分一一變換半群.

目前，對(duì)具有保序性質(zhì)變換半群極大子半群的研究已有很多結(jié)果［3－7］.文獻(xiàn)［3］給出了保序變換半群On的具有某種性質(zhì)的極大子半群；文獻(xiàn)［4］刻畫(huà)了有限保序部分一一變換半群極大逆子半群的完全分類(lèi)；文獻(xiàn)［5］討論了奇異保序變換半群的極大正則子半群；文獻(xiàn)［6］給出了有限部分保序變換半群POn的具有某種性質(zhì)的極大子半群；文獻(xiàn)［7］研究了保序部分變換半群POn的極大子半帶.

文獻(xiàn)［8］引入了保E＊關(guān)系部分一一變換半群.設(shè)X為有限集合，E為X 上的等價(jià)關(guān)系，且IX為X上的對(duì)稱(chēng)逆半群.令

IE＊（X）＝ ｛f∈IX：對(duì)任意的x，y∈dom（f），（x，y）∈E當(dāng)且僅當(dāng)（f（x），f（y））∈E｝，則IE＊（X）為IX的逆子半群，稱(chēng)為保E＊關(guān)系部分一一變換半群.文獻(xiàn)［8］討論了它的Green關(guān)系與秩.本文在文獻(xiàn)［8］與文獻(xiàn)［4］的基礎(chǔ)上，將保E＊關(guān)系與有序性引入到對(duì)稱(chēng)逆半群中，考慮一類(lèi)新的半群，即E類(lèi)保序嚴(yán)格部分一一變換半群.令X為有限集合，E為X上的等價(jià)關(guān)系，且IE＊（X）為保E＊關(guān)系部分一一變換半群.設(shè)f∈IE＊（X），任取x，y∈dom（f），若（x，y）∈E，x≥y 當(dāng)且僅當(dāng)（f（x），f（y））∈E，f（x）≥f（y），則稱(chēng)f為（X 上的）E類(lèi)保序部分一一變換.令OIE＊（X）為所有X 上的E類(lèi)保序嚴(yán)格部分一一變換之集，易驗(yàn)證OIE＊（X）是IE＊（X）（IX）的逆子半群，稱(chēng)為E類(lèi)保序嚴(yán)格部分一一變換半群.

任取x，y∈X，若x≤y，定義［x，y］＝｛z∈X：x≤z≤y｝.對(duì)于一般情形，即對(duì)任意的有限全序集X和X上的任意等價(jià)關(guān)系，很難描述半群OIE＊（X）的結(jié)構(gòu).因此，先考慮一種特殊情形.本文總假設(shè)X＝｛1，2，…，nm｝（n≥3，m≥2）為全序集，E為X 上的等價(jià)關(guān)系，滿(mǎn)足

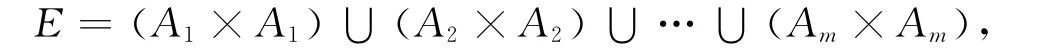
其中Ai＝［（i－1）n＋1，in］，i＝1，2，…，m.對(duì)于兩個(gè)變換的復(fù)合表示為gf：首先作用f，然后作用g.

設(shè)S是OIE＊（X）的逆子半群.若S滿(mǎn)足：對(duì)OIE＊（X）任意的逆子半群T，有S?T?T＝OIE＊（X），則稱(chēng)S是OIE＊（X）的一個(gè)極大逆子半群.本文在上述全序集與等價(jià)關(guān)系下討論OIE＊（X）的極大逆子半群.

1 預(yù)備知識(shí)

根據(jù)文獻(xiàn)［8］的結(jié)果，IE＊（X）的Green關(guān)系有如下刻畫(huà)：fRg 當(dāng)且僅當(dāng)Im（f）＝Im（g），fLg 當(dāng)且僅當(dāng)dom（f）＝dom（g），fHg當(dāng)且僅當(dāng)Im（f）＝Im（g）且dom（f）＝dom（g）.

由于任意半群及其正則子半群的Green關(guān)系中R，L，H 關(guān)系是一致的，注意到OIE＊（X）是IE＊（X）的正則子半群（因?yàn)镺IE＊（X）是IE＊（X）的逆子半群），則下列引理成立：

引理1 對(duì)任意的f，g∈OIE＊（X），fRg 當(dāng)且僅當(dāng)Im（f）＝Im（g），fLg 當(dāng)且僅當(dāng)dom（f）＝dom（g），fHg當(dāng)且僅當(dāng)Im（f）＝Im（g）且dom（f）＝dom（g）.

為敘述方便，在OIE＊（X）上引入如下二元關(guān)系.

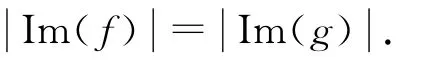
引理2 JΔ是OIE＊（X）上的等價(jià)關(guān)系，且H?JΔ，L?JΔ，R?JΔ.

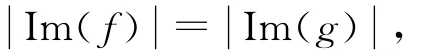
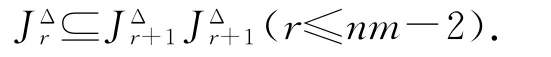
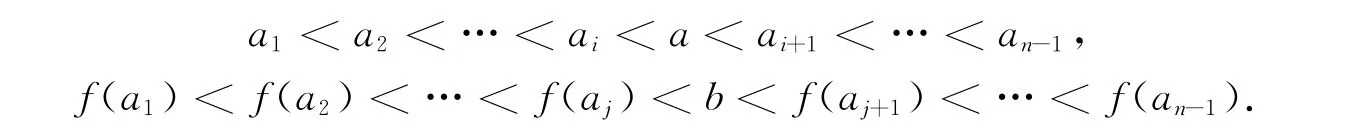
下面分3種情況討論.

②i＜j.令

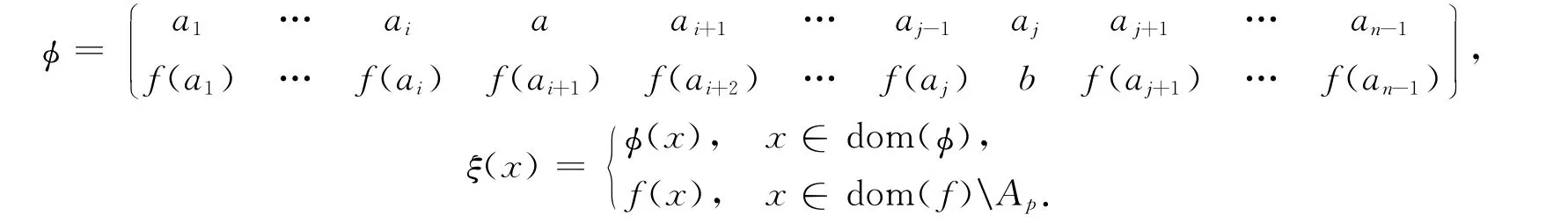
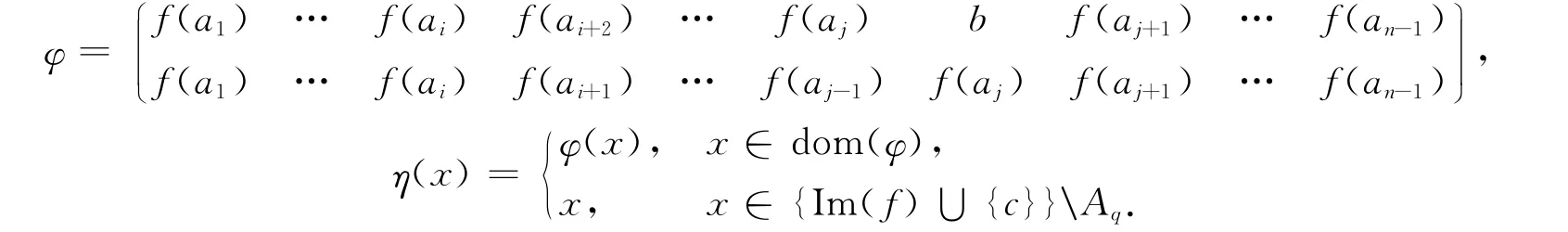
下證f＝ηξ.由η，ξ的定義，易驗(yàn)證dom（ηξ）＝dom（f），且

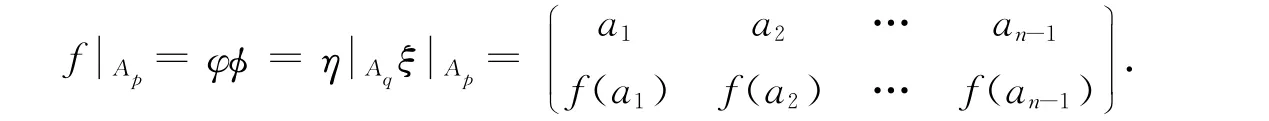
此外，考慮當(dāng)x∈dom（f）＼Ap時(shí)，ηξ（x）＝η（f（x））＝f（x）.故f＝ηξ.

③i＞j.證明類(lèi)似于②的證明.

設(shè)

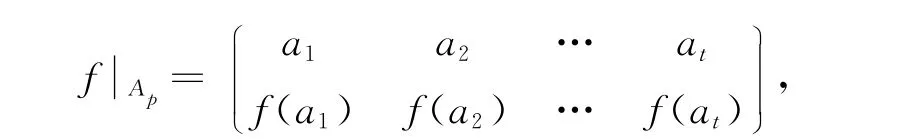
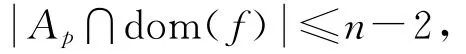
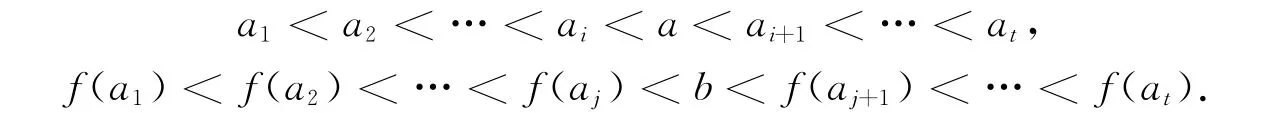
①i＝j(luò).證明類(lèi)似于情形1）中①的證明.

②i＜j.令

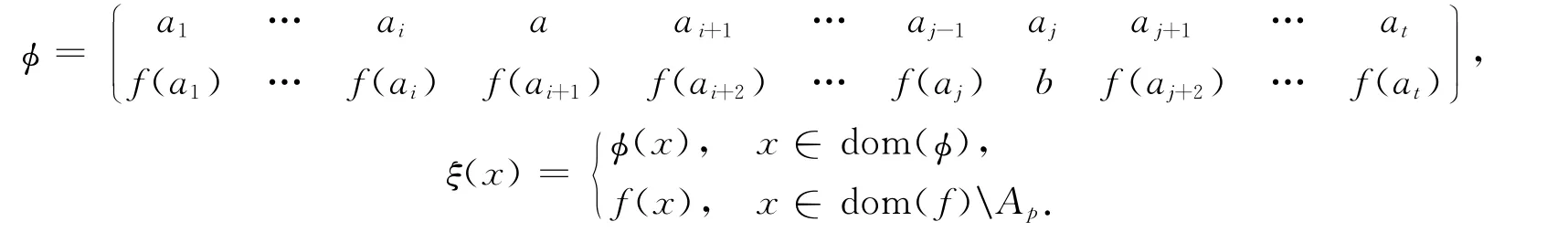
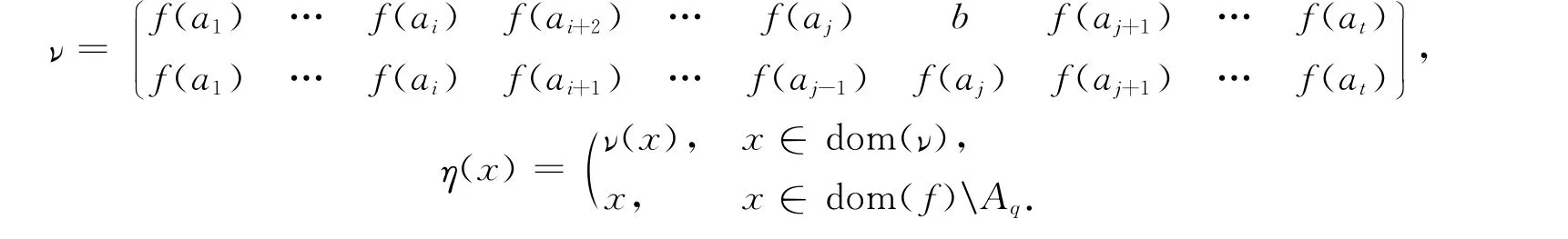
下證f＝ηξ.由ξ，η的定義，易驗(yàn)證dom（ηξ）＝dom（f），且

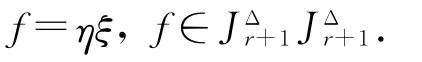
③i＞j.證明類(lèi)似于②的證明.

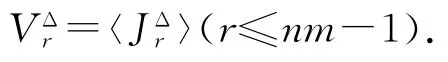
易知OIE＊（X）的頂端JΔ類(lèi)有如下nm個(gè)L類(lèi)與nm個(gè)R類(lèi)：

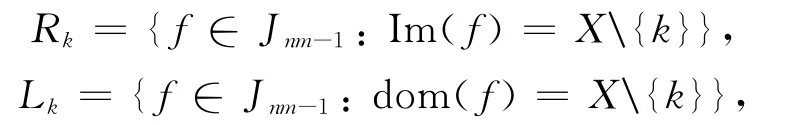
其中1≤k≤nm.用Hij表示Rj與Li所確定的H 類(lèi)Li∩Rj.注意到OIE＊（X）中元素的有序性，則OIE＊（X）的冪等元只含于Hii，且Hii中只含有唯一的冪等元（此冪等元為X＼｛i｝上的恒等變換）.

2 主要結(jié)果

定理1 設(shè)X＝｛1，2，…，nm｝（n≥2，m≥3），若（Σ，Λ）是X的一個(gè)二劃分（即Σ∪Λ＝X，Σ∩Λ＝?），則

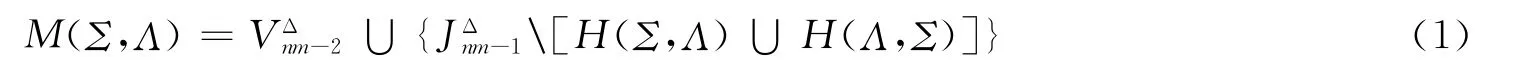
為OIE＊（X）的極大逆子半群.反之，對(duì)OIE＊（X）的任一極大逆子半群M，存在X的某個(gè)二劃分（Σ，Λ），使得M＝M（Σ，Λ）.

證明：1）證明設(shè)X＝｛1，2，…，nm｝（n≥2，m≥3），若（Σ，Λ）是X 的一個(gè)二劃分（即Σ∪Λ＝X，Σ∩Λ＝?），則式（1）為OIE＊（X）的極大逆子半群.

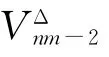
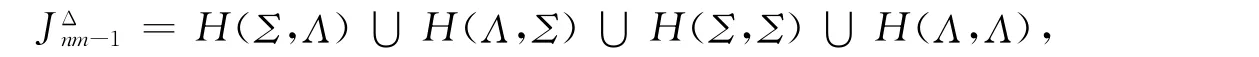
知f，g∈H（Σ，Σ）∪H（Λ，Λ）.設(shè)f∈Hij，g∈Hks（i，j，k，s∈X）.若f，g∈H（Σ，Σ），知i，j，k，s∈Σ，則易驗(yàn)證gf∈H（Σ，Σ）或gf∈.若f，g∈H（Λ，Λ），同理gf∈H（Λ，Λ）或gf∈.若f∈H（Σ，Σ），g∈H（Λ，Λ），由于（Λ，Σ）是一個(gè)二劃分，則gh∈.若f∈H（Λ，Λ），g∈H（Σ，Σ），同理gh∈.從而M（Σ，Λ）是OIE＊（X）的一個(gè)子半群.

其次，M（Σ，Λ）為 OIE＊（X）的逆子半群.對(duì)任意的f∈M（Σ，Λ），下證f 的唯一逆元f－1∈M（Σ，Λ）.由于是OIE＊（X）的逆子半群，可設(shè)f∈H（Σ，Σ）∪H（Λ，Λ）.由對(duì)稱(chēng)性，不妨設(shè)f∈H（Λ，Λ），則存在i，j∈Λ，使得f∈Hij.從而f在IX中的唯一逆元f－1∈Hji?H（Λ，Λ）?M（Σ，Λ），進(jìn)而 M（Σ，Λ）是OIE＊（X）的一個(gè)逆子半群.

最后，證明M（Σ，Λ）為OIE＊（X）的極大逆子半群.設(shè)S為OIE＊（X）的任一個(gè)真包含 M（Σ，Λ）的逆子半群，則存在g?M（Σ，Λ）且g∈S∩［H（Σ，Λ）∪H（Λ，Σ）］.由對(duì)稱(chēng)性，不妨設(shè)g∈H（Σ，Λ），則存在k∈Σ，s∈Λ，使得g∈Hks.注意到S是OIE＊（X）的逆子半群，可知g在OIE＊（X）的唯一逆元g－1在H（Λ，Σ）中.任取f∈H（Σ，Λ），不妨設(shè)f∈Hij（i∈Σ，j∈Λ），則存在h∈Hik，t∈Hsj，使得f＝tgh.從而H（Σ，Λ）?H（Λ，Λ）gH（Σ，Σ）?S.同理可證，H（Λ，Σ）?H（Σ，Σ）g－1H（Λ，Λ）?S，因此S＝OIE＊（X）.綜上所述，M（Σ，Λ）為OIE＊（X）的一個(gè)極大逆子半群.

2）證明對(duì)OIE＊（X）的任一極大逆子半群M，存在X的某個(gè)二劃分（Σ，Λ），使得M＝M（Σ，Λ）.

首先，證明對(duì)OIE＊（X）的任意極大逆子半群 M，都有 Hii?M（i∈｛1，2，…，nm｝）.

① 若存在i∈｛1，2，…，nm｝，使得 Hii∩M＝?，從而 M∩Li＝? 且M∩Ri＝?.令Σ1＝｛i｝，Λ1＝X＼Σ1.顯然，M（Σ1，Λ1）是OIE＊（X）的極大逆子半群.注意到 Hii?M（Σ1，Λ1），知 M 真包含于M（Σ1，Λ1），這與極大性矛盾，從而Hii?M.

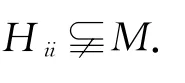
其次，證明若f∈M∩Hij（i，j∈｛1，2，…，nm｝），則Hij?M.由于Hjj∈M，則Hij?Hjjf?M.

最后，證明對(duì)OIE＊知（X）的任一極大逆子半群 M，存在X 的某個(gè)二劃分（Σ，Λ），使得M＝M（Σ，Λ）.由于冪等元只含在Hii（1≤i≤nm）中，且 Hii?M（i∈｛1，2，…，nm｝），故存在非冪等元f∈，但f?M.不妨設(shè)f∈Hks，則f∈Rk.Rk中有nm個(gè)R類(lèi)：Hk1，Hk2，…，Hk（nm）.注意到若f∈M∩Hij（i，j∈｛1，2，…，nm｝），則 Hij?M，從而對(duì)任意的 H 類(lèi)Hij有Hij?M 或Hij∩M＝?（j∈｛1，2，…，nm｝）.設(shè) 在 Rk中 與 M 相 交 為 ? 的 H 類(lèi) 有q 個(gè)，記 為 Hki1，Hki2，…，Hkiq.令Λ＝｛i1，i2，…，iq｝，Σ＝X＼Λ.下 證 M ＝M （Σ，Λ）.由 M 與 M （Σ，Λ）的 極 大 性， 只 需 證 明［H（Σ，Λ）∪H（Λ，Σ）］∩M＝?.不妨設(shè)存在f∈M∩H（Σ，Λ），即存在i∈Σ，r∈Λ，使得f∈M∩Hir，從而Hir?M.由i∈Σ，則Hki?M.易見(jiàn)HirHki＝Hkr，從而Hkr?M，這與r∈Λ矛盾.故H（Σ，Λ）∩M＝?.同理可證，H（Λ，Σ）∩M＝?，從而［H（Σ，Λ）∪H（Λ，Σ）］∩M＝?.注意到（Σ，Λ）為X的一個(gè)二劃分，知M（Σ，Λ）是OIE＊（X）的一個(gè)極大逆子半群.由M?M（Λ，Σ）且M 具有極大性，則M＝M（Λ，Σ）.

綜上所述結(jié)論成立.

［1］Gomes G M S，Howie J M.On the Ranks of Certain Semigruops of Order－Preserving Transformations ［J］.Semigroup Forum，1992，45（1）：272－282.

［2］Fernandes V H.The Monoid of All Injective Order－Preserving Partial Transformation on a Finite Chain ［J］.Semigroup Forum，2001，62（2）：178－204.

［3］YANG Xiuliang，LU Chunghan.Maximal Properties of Some Subsemigroups in Finite Order－Preserving Transformation Semigroups［J］.Communication in Algebra，2000，28（7）：3125－3135.

［4］徐波.關(guān)于有限保序部分一一變換半群的極大逆子半群 ［J］.貴州師范大學(xué)學(xué)報(bào)：自然科學(xué)版，2007，25（1）：72－73.（XU Bo.On Maxinal Inverse Subsemigroups of Certain Semigroups of Order－Preserving Partail One－One Transformation［J］.Journal of Guizhou Normal University：Natual Sciences，2007，25（1）：72－73.）

［5］許新齋，孟玲.奇異保序變換半群的極大正則子半群 ［J］.純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)，2009，25（3）：508－511.（XU Xinzhai，MENG Ling.The Maximal Regular Subsemigroups of Singular Order－Preserving Transformation Semigroups［J］.Pure and Applied Mathematics，2009，25（3）：508－511.）

［6］XU Bo，ZHAO Ping，LI Junyang.Maximal Properties of Some Subsemigroups in Finite Singular Partial Order－Preserving Transformation Semigroups［J］.Journal of Mathematics，2010，30（4）：617－621.

［7］徐波，趙平.半群 POn的極大子半帶 ［J］.吉林大學(xué)學(xué)報(bào)：理學(xué)版，2012，50（3）：445－451.（XU Bo，ZHAO Ping.Maximal Subsemibands of the Semigroup POn［J］.Journal of Jilin University：Science Edition，2012，50（3）：445－451.）

［8］龍偉鋒，游泰杰，龍偉芳，等.保E＊關(guān)系的部分一一變換半群 ［J］.西南大學(xué)學(xué)報(bào)：自然科學(xué)學(xué)報(bào)，2013，35（4）：63－66.（LONG Weifeng，YOU Taijie，LONG Weifang，et al.The Rank of Semigroup of Injective E＊－Preserving Partial Transformations［J］.Journal of Southwest University：Natual Science Edition，2013，35（4）：63－66.）

［9］Howie J M.An Introduction to Semigrpoup Theory［M］.London：Academic Press，1976.