分數階半正邊值問題一個正解的存在性定理

王麗穎，許曉婕

（1.白城師范學院 數學學院，吉林 白城137000；2.中國石油大學（華東）理學院，山東 青島266555）

考慮分數階半正邊值問題：

分數階微分方程在數學、力學、分數控制系統與分數控制器、各種電子回路以及回歸模型等領域，特別是與分形維數有關的物理與工程方面應用廣泛［1－8］.文獻［9］應用Leray－Schauder非線性抉擇、錐不動點定理和混合單調算子理論研究了奇異和非奇異邊值問題多重正解的存在性，并給出了奇異問題正解的唯一性，考慮了非線性項正的結果，即f：（0，1）×［0，＋∞）→［0，＋∞）.本文考慮“半正”問題，即存在M≥0，使得f：（0，1）×［0，＋∞）→［－M，＋∞）.

下面給出分數階微分方程邊值問題的格林函數及性質.

引理1［9］給定h∈C［0，1］和3＜α≤4，方程

稱為邊值問題（2）－（3）的格林函數.

引理2［9］由式（4）定義的格林函數G（t，s）滿足如下條件：

其中M0＝max｛α－1，（α－2）2｝.

本文主要利用Hammerstein積分方程和Krasnosel’skii錐不動點定理［10］.

引理3［10］令X是一個Banach空間，且P?X是X中的一個錐.假設Ω1，Ω2是X中的開子集，滿足0∈Ω1??Ω2，且令S：P→P是全連續算子，使得下列兩個條件之一成立：

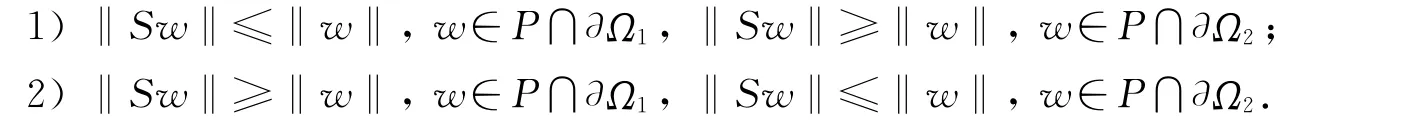
本文主要結果如下.

定理1 假設下列條件成立：

（H1）f：（0，1）×［0，＋∞）→（－∞，＋∞）是連續的；

（H3）存在非負函數h∈C（0，1）∩L1［0，1］，使得f（t，u）＋h（t）≥0，（t，u）∈（0，1）×［0，＋∞）；

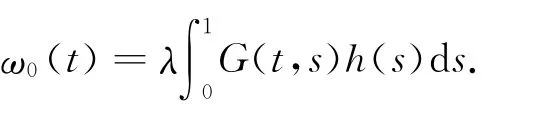
其中

事實上，如果0≤t≤s≤1，則

2）證明T：K→K是全連續的.

由假設（H1）～（H3），Tu∈C［0，1］.如果un∈K（n＝1，2，…），使得‖un－u‖→0，則當t∈（0，1）時，

由Lebesgue控制收斂定理可得

因此，T：K→C［0，1］是連續的.

令V?K 是有界集，且r2＝sup｛‖u‖：u∈V｝＋‖ω0‖＋1.如果u∈V，則max｛u（t）－ω0（t），0｝≤r2，0≤t≤1.由假設（H2），存在非負函數jr2∈L1［0，1］，使得f＊（t，（u（t）－ω0（t）））≤jr2（t），0＜t＜1.因此，

從而T（V）?C［0，1］是一致有界的.

由1），對任意的u∈V，

表明T（V）?C［0，1］是等度連續的.從而由 Arzela－Ascoli定理知，T：K→C［0，1］是全連續的.

另一方面，由引理2知，

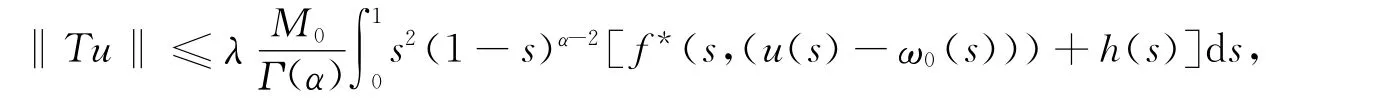
因此T（K）?K.

因為不動點等價于邊值問題

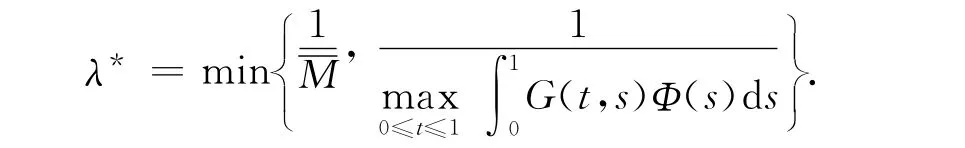
如果u∈?Ω（r3），則0≤max｛u（t）－ω0（t），0｝≤r3，0≤t≤1.因此f＊（t，（u（t）－ω0（t）））＋h（t）≤Φ（t），0＜t＜1.從而有

另一方面，當α≤t≤β時，

由Fatou引理可得

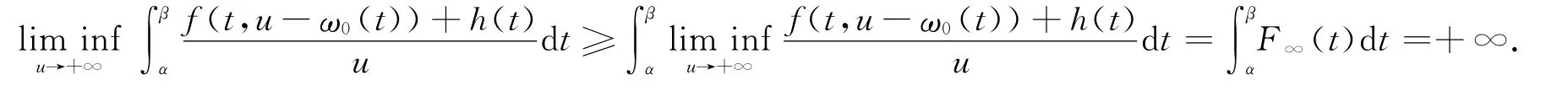
因此，存在一個正數r4＞r3，使得

如果u∈?Ω（r4），則‖u‖＝r4，且

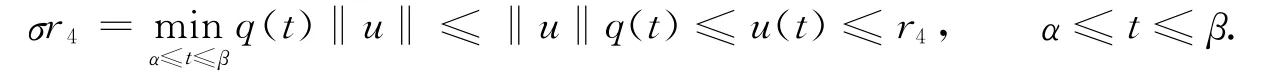
因此，

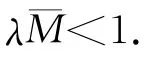
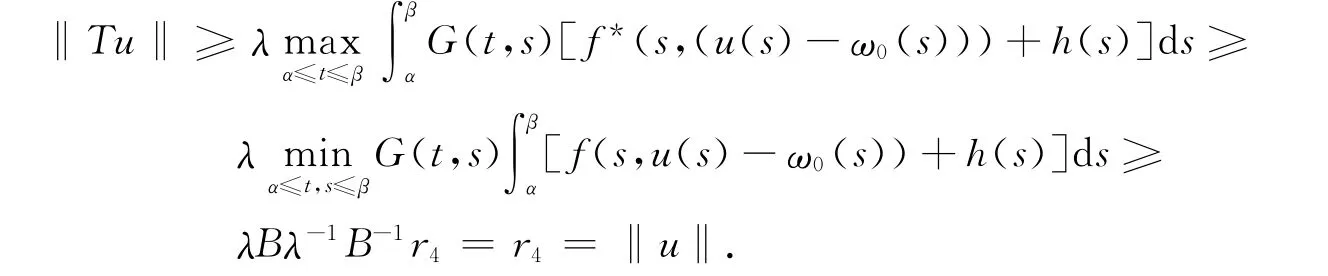
［1］Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations［M］.Amsterdam：Elsevier，2006.

［2］Oldham K B，Spanier J.The Fractional Calculus［M］.New York：Academic Press，1974.

［3］Ross B.Fractional Calculus and Its Applications［M］.Lecture Notes in Mathematics.Vol.475.Berlin：Springer－Verlag，1975.

［4］Nonnenmacher T F，Metzler R.On the Riemann－Liouvile Fractional Calculus and Some Recent Applications［J］.Fractals，1995（3）：557－566.

［5］Tatom F B.The Relationship between Fractional Calculus and Fractals［J］.Fractals，1995，3（1）：217－229.

［6］Podlubny I.Fractional Differential Equations ［M］.Mathematics in Science and Engineering.Vol.198.New York：Academic Press，1999.

［7］Samko S G，Kilbas A A，Marichev O I.Fractional Integral and Derivatives：Theorey and Applications［M］.Switzerland：Gordon and Breach Science Publishers，1993.

［8］Lakshmikantham V，Leela S，Vasundhar J，de.Theory of Fractional Dynamic Systems ［M］.Cambridge：Cambridge Academic Publishers，2009.

［9］XU Xiaojie，JIANG Daqing，YUAN Chengjun.Multiple Positive Solutions for Boundary Value Problem of a Nonlinear Fractional Differential Equation［J］.Nonlinear Analysis：Theory，Methods and Applications，2009，71：4676－4688.

［10］YAO Qingliu.An Existence Theorem of a Positive Solution to a Semipositone Sturm－Liouville Boundary Value Problem ［J］.Applied Mathematics Letters，2010，23（12）：1401－1406.