一類具有變指數偽拋物型方程解的存在唯一性

王長佳，代 群

（長春理工大學 理學院，長春130022）

0 引 言

考慮如下具有變指數偽拋物型方程的初邊值問題：

其中：Ω∈?N（N≥2）為一邊界充分光滑的有界開集；QT＝Ω×（0，T］；ΓT＝?Ω×（0，T］；p（x）為一給定的可測函數；q＞0為常數.

上述類型的方程通常稱為非線性偽拋物（pseudo－parabolic）型方程，它是一般拋物型方程的擴展，在聲學、電磁學、黏彈性力學和熱傳導等領域應用廣泛［1－3］，目前已取得許多研究結果，如文獻［4］利用Galerkin方法研究了一類算子形式偽拋物方程解的局部存在性；文獻［5］在加權Sobolev空間中給出了可解性條件并證明了解的唯一性，而且還對一些動力學問題的漸近性進行了討論；文獻［6］討論了一類具有雙非線性項的偽拋物型方程；文獻［7］對非線性項具有單調性的偽拋物型方程進行了研究.本文考慮具有變指數偽拋物型方程的初邊值問題（1），在參數滿足一定條件下，證明了此類問題弱解的存在唯一性.由于此類問題的解通常隸屬于變指數Lebesgue空間Lp（x）和變指數Sobolev空間Wk，p（x），在此類空間中許多經典的數學工具與技術不再適用，如平移算子的有界性、卷積不等式、與極大值算子和其他奇異積分算子相應的不等式，特別是龐加萊不等式以及Sobolev嵌入不等式在“模型式”下也將不再成立.

定義1 如果函數u（x，t）滿足下列條件：

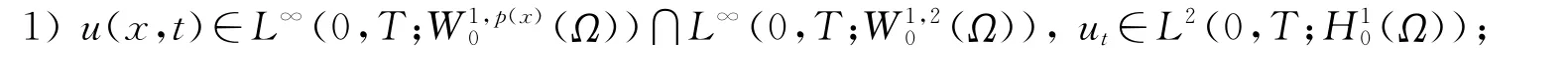
則u（x，t）稱為問題（1）的弱解.

注1 事實上，式（2）等價于下式［8］：

1 預備知識

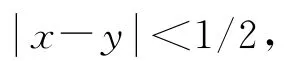
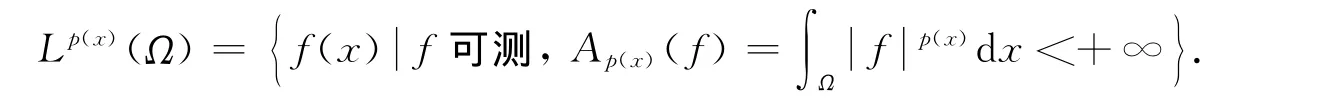
2）Lp（x）是可分的且其對偶空間為Lp′（x）（Ω），其中1／p′（x）＋1／p（x）＝1；對給定的f∈Lp（x），g∈Lp′（x），如下 H?lder不等式成立：

2 弱解的存在唯一性

2.1 近似解的構造

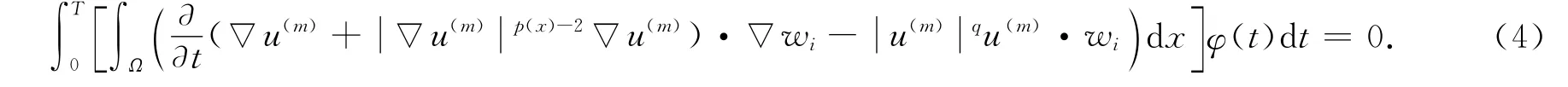
其中i＝1，2，…，m.

記

2.2 一致性先驗估計

由于

將式（7）代入式（8）并整理可得

將式（10）在（0，t）（0＜t＜T）上積分可得

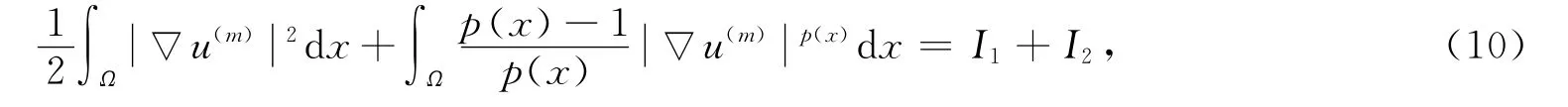
其中：

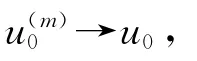
下面分兩種情形對Ym（t）進行估計.

情形1）p－＜q＋2＜2n／（n－2）.

將式（11）代入式（10）得

解微分不等式（12）可得

其中C，C1均為與m無關的常數.

情形2）p－≥q＋2（此時恒有q＋2≤np／（n－p－））.

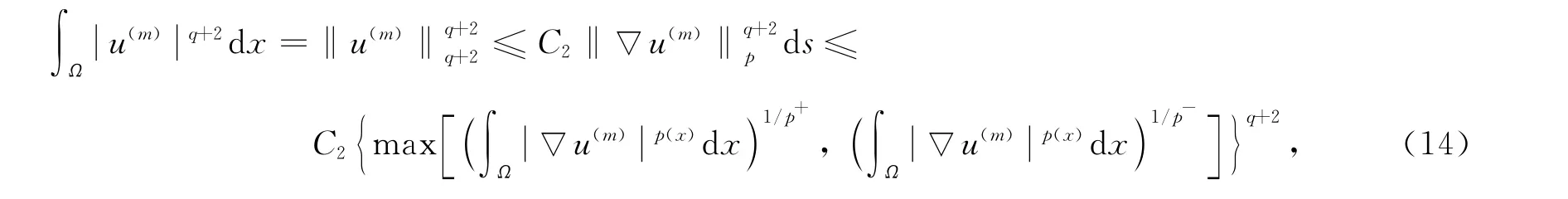
而

將式（14）～（16）代入式（8）得

其中：ν＋＝（q＋2）／p＋；ν－＝（q＋2）／p－.

如果ν±＜1，則解微分不等式（17）可得

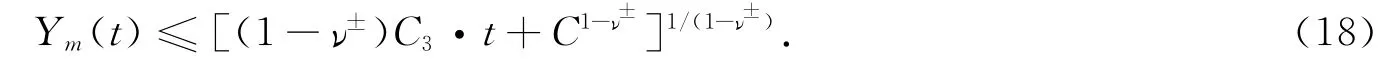
其中C，C3，C4均為與m無關的常數.

綜合式（13），（18），（19），可得Ym（t）≤C（T），即

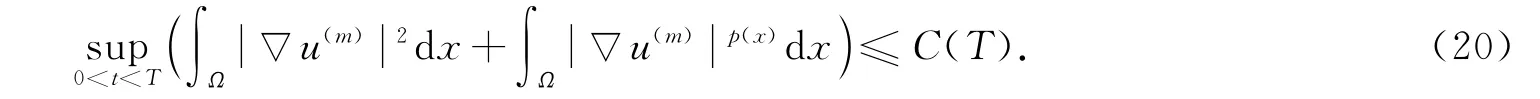
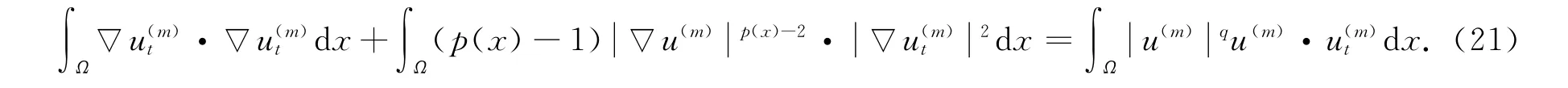
由于

將式（22），（23）代入式（21），并在（0，t）上積分可得

2.3 收斂性與解的存在性

由一致估計并結合 Aubin－Lions引理可得下述收斂性：u（m）?u弱＊收斂于L∞（0，T；W1，2∩W1，p（x）（Ω））；?u弱收斂于L2（0，T；W1，2（Ω））；u（m）（s）→u（s）強收斂于Lq＋2（Ω），a.e.s∈［0，T］；弱＊收斂于L∞（0，T；Lp′（x）（Ω））.

對固定的i∈?，令m→∞，可得

從而由弱上半連續性知

對任意的λ≥0，w∈W1，p（x）0，取v＝u－λw，則有

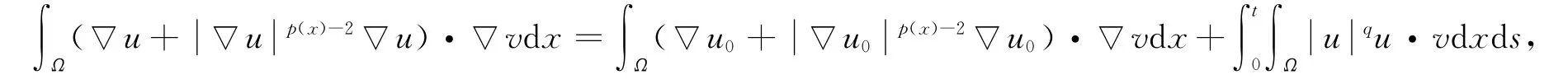
即在廣義函數意義下成立：

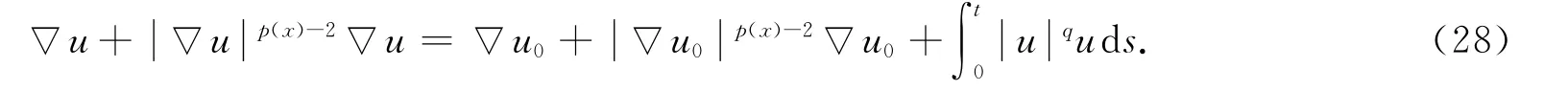
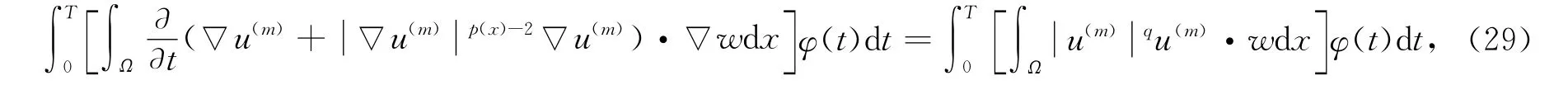
令m→∞對式（29）兩端取極限可得，對?w∈W1，p（x）0（Ω），φ（t）∈L2（0，T），有

2.4 唯一性

令u1，u2為問題（1）的兩個解，則由上述討論可知對?w∈W1，p（x）0（Ω），u1，u2滿足等式：

將式（30）－式（31），有

由u1，u2的有界性，由式（32）可得

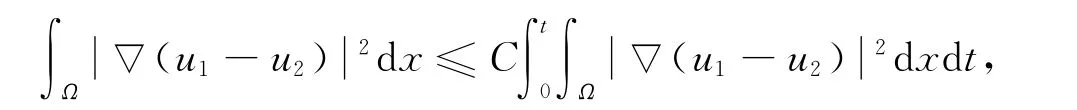
進而利用Gronwall不等式可得u1＝u2，a.e.（x，t）∈QT.

綜上，可得本文主要結果如下：

定理1 設Ω為一光滑有界區域，p（x）∈［p－，p＋］滿足條件（3），p－＞2，q＋2＜2n／（n－2）.

2）若q≤p－－2，則對?T∈（0，＋∞），方程（1）在（0，T）上存在定義1意義下的唯一弱解.

［1］Barenblatt I G，Bertsch M，Dal Passo R，et al.A Degenerate Pseudoparabolic Regularization of a Nonlinear Forward－Backward Heat Equation Arising in the Theory of Heat and Mass Exchange in Stably Stratified Turbulent Shear Flow ［J］.SIAM Journal on Mathematical Analysis，1993，24（6）：1414－1439.

［2］Bock I.On the Semidiscretization and Linearization of Pseudoparabolic Von Kármán System for Viscoelastic Plates［J］.Mathematical Methods in the Applied Sciences，2006，29（5）：557－573.

［3］Ptashnyk M.Pseudoparabolic Equations with Convection ［J］.IMA Journal of Applied Mathematics，2007，72（6）：912－922.

［4］Gajewski H，Gr?ger K，Zacharias K.Nichtlineare Operatorgleichungen und Operatordifferentialgleichungen［M］.Berlin：Akademie－Verlag，1974.

［5］Demidenko G V，Upsenskii S V.Partial Differential Equations and Systems Not Solvable with Respect to the Highest－Order Derivative［M］.New York：CRC Press，2003.

［6］Stefanelli U.On a Class of Doubly Nonlinear Nonlocal Evolution Equations［J］.Differential Integral Equations，2002，15（8）：897－1023.

［7］Showalter R E.Monotone Operators in Banach Space and Nonlinear Partial Differential Equations ［M］.Providence，RI：Amer Math Soc，1997.

［8］Al’shin A B，Korpusov M O，Sveshnikov A G.Blow－up in Nonlinear Sobolev Type Equations［M］.De Gruyter，Series：De Gruyter Series in Nonlinear Analysis and Applications 15.Berlin：Walter de Gruyter ＆Co.，2011.

［9］Diening L，Harjulehto P，H?st?P，et al.Lebesgue and Sobolev Spaces with Variable Exponents［M］.Berlin：Springer，2011.