線性互補問題與絕對值方程的轉(zhuǎn)化

雍龍泉，劉三陽，拓守恒，鄧方安，高 凱

（1.西安電子科技大學 數(shù)學與統(tǒng)計學院，西安710071；2.陜西理工學院 數(shù)學與計算機科學學院，陜西 漢中723001）

線性互補問題（linear complementarity problem，LCP）是一類應用廣泛的優(yōu)化問題，它為線性規(guī)劃和二次規(guī)劃提供了統(tǒng)一的研究框架，因此求解線性互補問題的有效算法備受關(guān)注［1－2］.對線性互補問題的研究，目前主要集中在理論與算法兩方面，前者主要研究其解的存在性、唯一性、穩(wěn)定性和靈敏度分析，后者主要建立其有效的求解方法和相應的收斂性分析.求解線性互補問題的算法有很多，經(jīng)典的有Lemke算法；近年來（針對單調(diào)線性互補）出現(xiàn)了一些具有多項式復雜性的算法，如投影法、內(nèi)點法、非光滑牛頓法、光滑牛頓法和迭代法等［3－7］.

絕對值方程（absolute value equation，AVE）等價于一個不可微的NP難優(yōu)化問題.目前對于絕對值方程的研究主要集中于其解的存在性和唯一性以及建立有效的算法并進行相應的收斂性分析［8－15］.

本文研究線性互補問題與絕對值方程之間的內(nèi)在關(guān)系，給出了二者的等價轉(zhuǎn)化，并進行了證明.本文用I表示單位矩陣，‖·‖表示2范數(shù)，⊥表示兩個向量正交：即

1 預備知識

定義1 如果對?z∈?n，都有zTMz≥0，則矩陣M∈?n×n稱為半正定矩陣；如果對?z∈?n，z≠0，都有zTMz＞0，則M稱為正定矩陣.這里定義的半正定矩陣與正定矩陣不限制對稱性［5，16－17］.

線性互補問題即求向量z∈?n，滿足Mz＋q≥0，z≥0，zT（Mz＋q）＝0，簡記為LCP（M，q）.

當矩陣M是半正定矩陣時，LCP（M，q）稱為單調(diào)線性互補問題［16］.

引理1［5］設矩陣M∈?n×n為一半正定矩陣，對于任意的q∈?n，若LCP（M，q）是可行的，則LCP（M，q）必有解，且其解集為凸集.

引理2［5］設矩陣M∈?n×n為一正定矩陣，則對于任意的q∈?n，LCP（M，q）有唯一解.

上述判定線性互補問題解存在的條件僅是充分條件，而非必要條件［17］.更多關(guān)于線性互補問題解存在的條件可參見文獻［5］.

引理3［8］絕對值方程

2 線性互補問題到絕對值方程的轉(zhuǎn)化

定理1 線性互補問題Mz＋q≥0，z≥0，zT（Mz＋q）＝0等價于如下絕對值方程：

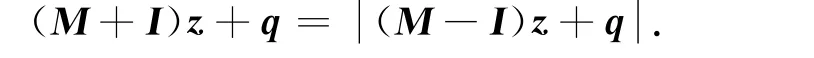
證明：對?a，b∈?，都有

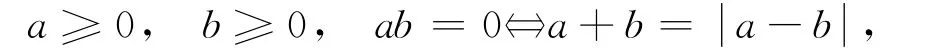
該結(jié)論對向量也成立.因此，令a＝Mz＋q，b＝z，則有

即

定理2 若1不是矩陣M的特征值，則LCP（M，q）等價于如下絕對值方程：

這里x＝（M－I）z＋q.

證明：利用定理1可知

由于1不是M 的一個特征值，故（M－I）－1存在.令x＝（M－I）z＋q，即z＝（M－I）－1（x－q），可得

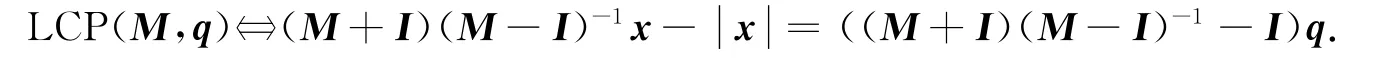
定理3 若1不是矩陣M的特征值，則LCP（M，q）等價于如下絕對值方程：

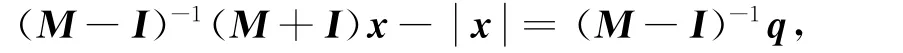
證明：令

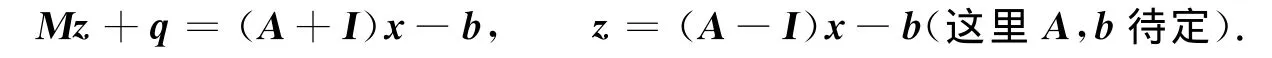
結(jié)合引理3，有

下面給出A，b的表達式.

把z＝（A－I）x－b代入Mz＋q＝（A＋I）x－b中，有

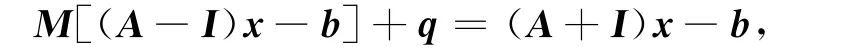
由于1不是M的一個特征值，故（M－I）－1存在.簡單計算可得

從而

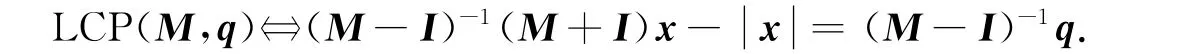
又由z＝（A－I）x－b得

證畢.

當1是矩陣M的特征值時，對線性互補問題中的M和q乘以某個正常數(shù)λ，使得1不是矩陣λM的特征值（此時線性互補問題的解不變），再應用定理2或定理3可把線性互補問題轉(zhuǎn)化為絕對值方程.

考慮LCP（M，q），其中：

M的特征值為

對于?z≠0，由于

因此矩陣M是正定矩陣，易求得該問題的唯一解為z＊＝（2.5，0.5，0，2.5）T.

由于1是矩陣M的特征值，因此定理2和定理3不能直接使用.令λ＝3，則λM 的特征值不為1，且LCP（λM，λq）與LCP（M，q）具有共同的最優(yōu)解z＊，而LCP（λM，λq）可應用定理2或定理3轉(zhuǎn)化為絕對值方程.

3 絕對值方程到線性互補問題的轉(zhuǎn)化

Prokopyev［21］給出了（在無任何條件下）絕對值方程轉(zhuǎn)化為線性互補問題的一種方法，但該轉(zhuǎn)化增加了問題的維數(shù)；胡勝龍等［22］通過重構(gòu)技巧（在無任何條件下）把絕對值方程轉(zhuǎn)化為線性互補問題，但該方法的實現(xiàn)有一定難度.

定理4（有條件轉(zhuǎn)化）若1不是A的特征值，則AVE等價于LCP（M，q）：

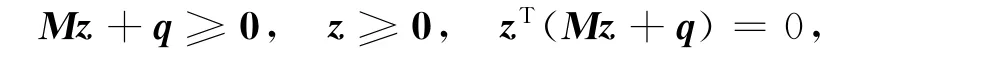
其中：z＝（A－I）x－b；M＝（A＋I）（A－I）－1；q＝（（A＋I）（A－I）－1－I）b.

證明：由于1不是A的一個特征值，故（A－I）－1存在.結(jié)合引理3，有

令z＝（A－I）x－b，即x＝（A－I）－1（z＋b），可得

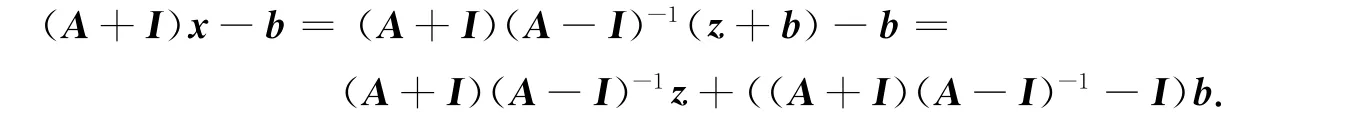
若令

則有

即

其中：z＝（A－I）x－b；M＝（A＋I）（A－I）－1；q＝（（A＋I）（A－I）－1－I）b.

推論1 若矩陣A的奇異值（即矩陣ATA特征值的非負平方根）都大于1，則矩陣M＝（A＋I）（A－I）－1是一個正定矩陣.

證明：若矩陣A的奇異值都大于1，則（A－I）－1存在（否則，?ξ≠0，使得（A－I）ξ＝0，即Aξ＝ξ，表明1是A的特征值，從而1也是A的奇異值，矛盾），且ATA的所有特征值都大于1，因此，對任意的z≠0都成立zT（ATA－I）z＞0.而

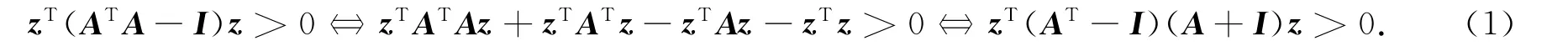
由于（A－I）－1存在，令z＝（A－I）－1v（z≠0，故v≠0），代入式（1）并整理得

即

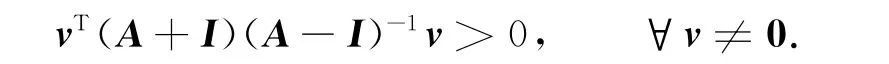
表明矩陣M＝（A＋I）（A－I）－1是一個正定矩陣.

矩陣A的奇異值都大于1?矩陣M＝（A＋I）（A－I）－1是一個正定矩陣?對應的LCP（M，q）具有唯一解?相應的AVE具有唯一解.

綜上可見，線性互補與絕對值方程具有密切的內(nèi)在聯(lián)系.基于上述對兩類問題的轉(zhuǎn)化，在求解任意絕對值方程時，都可以通過求解如下無約束優(yōu)化問題

獲得絕對值方程的解；在求解任意線性互補問題時，都可以通過求解如下無約束優(yōu)化問題

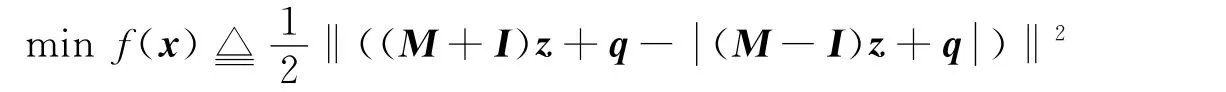
獲得線性互補問題的解.該方法對矩陣A或M 可以沒有任何限制，當目標函數(shù)值收斂到零，則達到最優(yōu)解；當目標函數(shù)值收斂不到零，則原問題可能無解；因此該方法具有較強的實用性.

［1］Billups S C，Murty K G.Complementarity Problems［J］.Journal of Computational and Applied Mathematics，2000，124：303－318.

［2］Cottle R W，PANG Jong－shi，Stone R E.The Linear Complementarity Problems［M］.San Diego：Academic Press，1992.

［3］Kojima M，Megiddo N，Noma T，et al.A Unified Approach to Interior Point Algorithms for Linear Complementary Problems：A Summary［J］.Operations Research Letters，1991，10（5）：247－254.

［4］Murty K G.Linear Complementarity，Linear and Nonlinear Programming［M］.Berlin：Heldermann Verlag，1988.

［5］韓繼業(yè)，修乃華，戚厚鐸.非線性互補理論與算法 ［M］.上海：上海科學技術(shù)出版社，2006：31－250.（HAN Jiye，XIU Naihua，QI Houduo.Theory and Algorithm for the Nonlinear Complementarity ［M］.Shanghai：Shanghai Science and Technology Press，2006：31－250.）

［6］YONG Longquan.Interior Point Algorithms for Monotone Linear Complementarity Problem ［J］.ICIC Express Letters，2011，5（3）：775－781.

［7］YONG Longquan.Research on Linear Complementarity Problem and Related Application ［J］.Engineering Technology Press，2010（2）：287－290.

［8］Mangasarian O L，Meyer R R.Absolute Value Equations［J］.Linear Algebra Appl，2006，419（2／3）：359－367.

［9］Rohn J.An Algorithm for Solving the Absolute Value Equation［J］.Electronic Journal of Linear Algebra，2009，18：589－599.

［10］YONG Longquan，LIU Sanyang，ZHANG Shemin，et al.A New Method for Absolute Value Equations Based on Harmony Search Algorithm ［J］.ICIC Express Letters，Part B：Applications，2011，2（6）：1231－1236.

［11］雍龍泉，拓守恒.基于凝聚函數(shù)的擬牛頓算法求解絕對值方程 ［J］.系統(tǒng)科學與數(shù)學，2012，32（11）：1427－1436.（YONG Longquan，TUO Shouheng.Quasi－Newton Method to Absolute Value Equations Based on Aggregate Function［J］.Journal of Systems Science and Mathematical Sciences，2012，32（11）：1427－1436.）

［12］YONG Longquan.An Iterative Method for Absolute Value Equations Problem ［J］.Information，2013，16（1）：7－12.

［13］雍龍泉，劉三陽，拓守恒，等.具有2n個解的絕對值方程問題 ［J］.吉林大學學報：理學版，2013，51（3）：383－388.（YONG Longquan，LIU Sanyang，TUO Shouheng，et al.Absolute Value Equations with 2n－Solutions［J］.Journal of Jilin University：Science Edition，2013，51（3）：383－388.）

［14］Caccetta L，BIAO Qu，ZHOU Guanglu.A Globally and Quadratically Convergent Method for Absolute Value Equations［J］.Computational Optimization and Applications，2011，48（1）：45－58.

［15］雍龍泉，張社民，張建科，等.絕對值方程研究進展 ［J］.陜西理工學院學報：自然科學版，2012，28（1）：33－38.（YONG Longquan，ZHANG Shemin，ZHANG Jianke，et al.Advance in the Study of Absolute Value Equations［J］.Journal of Shaanxi University of Technology：Natural Science Edition，2012，28（1）：33－38.）

［16］雍龍泉，鄧方安，陳濤.單調(diào)線性互補問題的一種內(nèi)點算法 ［J］.數(shù)學雜志，2009，29（5）：681－686.（YONG Longquan，DENG Fang’an，CHEN Tao.An Interior Point Method for Solving Monotone Linear Complementarity Problems［J］.Journal of Math，2009，29（5）：681－686.）

［17］雍龍泉，鄧方安.線性互補問題中矩陣正定性判別的2點注記 ［J］.吉首大學學報：自然科學版，2009，30（1）：33－35.（YONG Longquan，DENG Fang’an.Two Notes on Positiveness Judgement of Matrix in Linear Complementarity Problem ［J］.Journal of Jishou University：Natural Science Edition，2009，30（1）：33－35.）

［19］魏慶舉.絕對值方程的廣義牛頓算法及其收斂性 ［D］.北京：北京交通大學，2009.（WEI Qingju.A Generalized Newton Method and Its Convergence for Absolute Value Equations［D］.Beijing：Beijing Jiaotong University，2009.）

［20］雍龍泉.絕對值方程研究綜述 ［J］.陜西理工學院學報：自然科學版，2013，29（6）：25－30.（YONG Longquan.Review of Absolute Value Equation［J］.Journal of Shaanxi University of Technology：Natural Science Edition，2013，29（6）：25－30.）

［21］Prokopyev O.On Equivalent Reformulations for Absolute Value Equations［J］.Computational Optimization and Applications，2009，44（3）：363－372.

［22］HU Shenglong，HUANG Zhenghai.A Note on Absolute Value Equations ［J］.Optimization Letters，2010，4（3）：417－424.