基于樣本修整和支持向量機(jī)算法的并網(wǎng)風(fēng)電機(jī)組運(yùn)行特性研究

王吉東， 許 昌， 王 欣， 韓星星， 鄭 源， 劉德有

（河海大學(xué) 能源與電氣學(xué)院，南京 210098）

由于風(fēng)資源的不可預(yù)測(cè)性以及機(jī)械、電氣等多重因素的影響［1］，風(fēng)電機(jī)組運(yùn)行工況復(fù)雜多變，系統(tǒng)具有明顯的非線性、隨機(jī)性和強(qiáng)耦合性，因此，很難建立精確的物理模型［2］.在傳統(tǒng)的風(fēng)力機(jī)建模中，風(fēng)能計(jì)算通常采用文獻(xiàn)［3］中提供的風(fēng)能利用系數(shù)Cp的經(jīng)驗(yàn)公式，由于機(jī)組類型、參數(shù)等差異，該公式不能適用于不同機(jī)組，所以，采用經(jīng)驗(yàn)公式建立的控制理論缺乏實(shí)用價(jià)值.而以實(shí)際運(yùn)行數(shù)據(jù)為基礎(chǔ)，通過(guò)現(xiàn)代智能算法探究風(fēng)電機(jī)組的實(shí)際運(yùn)行規(guī)律，為風(fēng)力發(fā)電系統(tǒng)建模與控制提供了新思路.

現(xiàn)代智能建模領(lǐng)域應(yīng)用最為廣泛的是人工神經(jīng)網(wǎng)絡(luò)算法，而神經(jīng)網(wǎng)絡(luò)模型中最常用的是BP（back propagation）神經(jīng)網(wǎng)絡(luò)，該方法結(jié)構(gòu)簡(jiǎn)單、處理非線性問(wèn)題能力強(qiáng)，但是，由于其基于經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化原則（ERM），預(yù)測(cè)時(shí)常出現(xiàn)局部誤差過(guò)大的問(wèn)題，對(duì)于小樣本模型無(wú)法達(dá)到理想的預(yù)測(cè)精度［4］.Vapnik在統(tǒng)計(jì)學(xué)習(xí)理論基礎(chǔ)上提出的支持向量機(jī)（SVM）是一類新型的機(jī)器學(xué)習(xí)算法，它基于結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則（SRM），克服了常規(guī)神經(jīng)網(wǎng)絡(luò)算法的缺陷，具有預(yù)測(cè)精度高、泛化能力強(qiáng)、能收斂于全局最優(yōu)等特點(diǎn)［5］.文獻(xiàn)［6－7］針對(duì)不同類型的訓(xùn)練數(shù)據(jù)，討論了SVM 核函數(shù)的選擇方法.文獻(xiàn)［8］討論了SVM中懲罰參數(shù)C 和預(yù)設(shè)誤差ε 對(duì)回歸函數(shù)的影響.文獻(xiàn)［9－11］分別介紹了利用雙線性搜索法、網(wǎng)格搜索法、雙線性網(wǎng)格搜索法、二分法及粒子群算法等對(duì)SVM 參數(shù)進(jìn)行優(yōu)化的方法.SVM 算法用于回歸估計(jì)時(shí)輸出為實(shí)函數(shù)集，多用在非線性函數(shù)逼近、時(shí)間序列預(yù)測(cè)、過(guò)程建模和控制領(lǐng)域［12－14］.

本文從歷史運(yùn)行數(shù)據(jù)入手，針對(duì)風(fēng)電機(jī)組實(shí)際運(yùn)行特點(diǎn)，對(duì)原始樣本進(jìn)行分類、剔除壞點(diǎn)、歸一化等處理，得到新的訓(xùn)練樣本，大大增強(qiáng)各個(gè)輸入變量和目標(biāo)值之間的相關(guān)性，克服了支持向量機(jī)在處理龐大雜亂數(shù)據(jù)時(shí)速度慢、預(yù)測(cè)精度低的缺點(diǎn)［15］.通過(guò)對(duì)實(shí)際樣本訓(xùn)練分析，比較樣本修整前后和分別運(yùn)用SVM 算法與BP神經(jīng)網(wǎng)絡(luò)算法的訓(xùn)練結(jié)果，證明本文提出的方法能夠縮短訓(xùn)練時(shí)間、具有更高的訓(xùn)練精度和預(yù)測(cè)精度，是一種切實(shí)有效的風(fēng)電機(jī)組系統(tǒng)辨識(shí)方法.

1 樣本預(yù)處理方法

圖1是風(fēng)力機(jī)標(biāo)準(zhǔn)運(yùn)行曲線，據(jù)此可以看出，在運(yùn)行點(diǎn)B 并網(wǎng)以后，風(fēng)電機(jī)組運(yùn)行狀態(tài)可分成兩段：a.額定風(fēng)速以下的部分負(fù)荷區(qū)，控制風(fēng)力機(jī)轉(zhuǎn)速變化，跟蹤最佳葉尖速比實(shí)現(xiàn)最大風(fēng)能捕獲；b.額定風(fēng)速以上的滿負(fù)荷區(qū)，調(diào)節(jié)槳距角，限制風(fēng)力機(jī)轉(zhuǎn)速和氣動(dòng)功率捕獲，確保發(fā)電機(jī)組輸出功率穩(wěn)定在額定值.

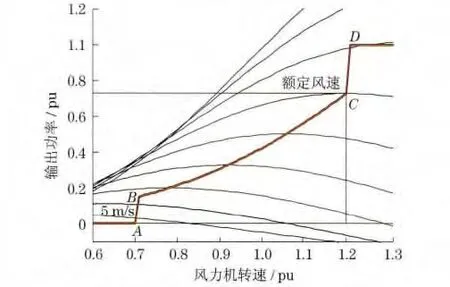
圖1 風(fēng)力機(jī)標(biāo)準(zhǔn)運(yùn)行特性曲線Fig.1 Standard operation characteristic curve of wind turbine

在圖1中，pu為標(biāo)幺值，風(fēng)力機(jī)轉(zhuǎn)速和輸出功率分別以發(fā)電機(jī)同步轉(zhuǎn)速和風(fēng)力機(jī)額定功率作為基準(zhǔn)值.

本文的研究目的是利用風(fēng)電場(chǎng)實(shí)測(cè)數(shù)據(jù)，在低風(fēng)速時(shí)，建立風(fēng)力機(jī)轉(zhuǎn)速給定值輸出模型；在高風(fēng)速時(shí)，建立實(shí)際的槳距角給定值輸出模型.得到轉(zhuǎn)速控制和槳距角控制的給定值，為采用智能轉(zhuǎn)速控制器和槳距角控制器取代傳統(tǒng)PID 控制器提供理論支持.

對(duì)樣本進(jìn)行預(yù)處理：

a.提取樣本.根據(jù)實(shí)際運(yùn)行特性按工況提取所需樣本數(shù)據(jù)，提取額定風(fēng)速以下的部分負(fù)荷區(qū)數(shù)據(jù)作為樣本I，提取額定風(fēng)速以上的滿負(fù)荷區(qū)數(shù)據(jù)作為樣本II.

b.剔除壞點(diǎn).訓(xùn)練樣本包括輸入和輸出樣本數(shù)據(jù)，輸入樣本Xk＝（xk1，xk2，…，xki，…，xkm），其中，主要變量設(shè)為M（本文中指風(fēng)速v）；輸出樣本Th＝（th1，th2，…，thj，…，thm），根據(jù)訓(xùn)練目標(biāo)不同，選定輸出的目標(biāo)變量T（輸出功率P、風(fēng)力機(jī)轉(zhuǎn)速ω 或槳距角β）.

在樣本中存在一些不合理的數(shù)據(jù)點(diǎn)，會(huì)嚴(yán)重影響訓(xùn)練和預(yù)測(cè)的精度，這些點(diǎn)大致分為兩類：第一類是由于設(shè)備檢測(cè)或數(shù)據(jù)記錄錯(cuò)誤等因素產(chǎn)生的與實(shí)際運(yùn)行規(guī)律相悖的數(shù)據(jù)點(diǎn)；第二類是由于機(jī)組慣性或湍流風(fēng)速過(guò)大等原因引起的嚴(yán)重偏離最優(yōu)運(yùn)行曲線的數(shù)據(jù)點(diǎn).對(duì)兩種“壞點(diǎn)”進(jìn)行數(shù)學(xué)定義，對(duì)于樣本內(nèi)的第i個(gè)數(shù)據(jù)點(diǎn)：

第一類

第二類

式中，δ為平整度，可自主設(shè)定.

以江蘇省某風(fēng)電場(chǎng)額定風(fēng)速以下的運(yùn)行數(shù)據(jù)為例，選擇風(fēng)速v 作為樣本主要屬性，輸出功率P 作為目標(biāo)變量，平整度δ＝15%.按照式（1）和式（2）逐個(gè)剔除樣本中的“壞點(diǎn)”，圖2（a）和2（b）分別顯示了樣本處理前后的數(shù)據(jù)點(diǎn)分布情況，比較發(fā)現(xiàn)，剔除壞點(diǎn)后樣本得到有效簡(jiǎn)化，數(shù)據(jù)間具有更強(qiáng)的相關(guān)性.

圖2 剔除壞點(diǎn)前后樣本數(shù)據(jù)比較Fig.2 Comparison of initial data and reduced data

c.數(shù)據(jù)歸一化處理.為了避免各指標(biāo)的數(shù)值之間相差過(guò)大影響學(xué)習(xí)訓(xùn)練的速度，對(duì)歷史數(shù)據(jù)進(jìn)行規(guī)一化處理，即將原始數(shù)據(jù)經(jīng)過(guò)線性變化至［0，1］區(qū)間中，構(gòu)成訓(xùn)練數(shù)據(jù)集［16］.

2 支持向量機(jī)回歸算法

在支持向量機(jī)回歸方法中，分為線性回歸與非線性回歸.對(duì)于線性回歸問(wèn)題，根據(jù)給定的訓(xùn)練集樣本｛（x1，y1），（x2，y2），…，（xl，yl）｝，xi∈?n，yi∈?，i＝1，2，…，l.xi為輸入量，yi為對(duì)應(yīng)的輸出量，尋求一個(gè)反映樣本數(shù)據(jù)輸出和輸入的最優(yōu)函數(shù)關(guān)系f（x），并且對(duì)于預(yù)測(cè)集樣本的輸入量｛xl＋1，xl＋2，…，xm｝，能夠由該函數(shù)得出較為準(zhǔn)確的預(yù)測(cè)值｛yl＋1，yl＋2，…，ym｝.

函數(shù)“最優(yōu)”是指按照某一確定的誤差函數(shù)來(lái)計(jì)算，所得的函數(shù)關(guān)系對(duì)樣本數(shù)據(jù)集擬合的累計(jì)誤差最小，SVM 算法用于回歸估計(jì)采用ε－intensive損失函數(shù)作為誤差函數(shù)，形式為

訓(xùn)練學(xué)習(xí)的過(guò)程是構(gòu)造最優(yōu)的線性擬合函數(shù)f（x）＝wx＋b，其中，w∈?n，b∈?.根據(jù)結(jié)構(gòu)風(fēng)險(xiǎn)最小化原理，將訓(xùn)練過(guò)程進(jìn)行轉(zhuǎn)化，通過(guò)最小化目標(biāo)函數(shù)來(lái)訓(xùn)練w 和b［17］.

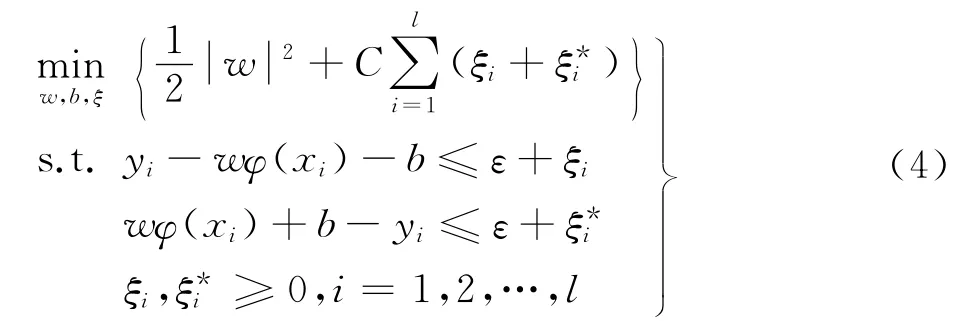
式（4）中第一項(xiàng)使擬合函數(shù)更為平坦，以提高泛化能力；第二項(xiàng)為減小誤差；懲罰參數(shù)C＞0，表示對(duì)超出預(yù)設(shè)誤差ε的樣本的懲罰程度，這是一個(gè)對(duì)偶二次凸規(guī)劃問(wèn)題，引入Lagrange函數(shù)，將式（4）的對(duì)偶最優(yōu)化問(wèn)題轉(zhuǎn)化為最大化目標(biāo)函數(shù)

約束條件為

參數(shù)b的求解，對(duì)于滿足0＜αi＜C條件的標(biāo)準(zhǔn)支持向量，有

式中，SV 表示標(biāo)準(zhǔn)支持向量的集合，包含所有在間隔區(qū)邊緣的訓(xùn)練樣本點(diǎn).

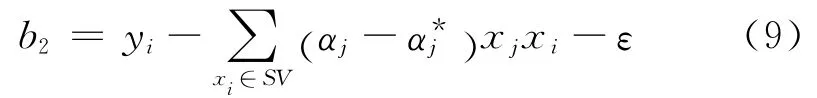
通過(guò)式（8）和式（9）對(duì)所有標(biāo)準(zhǔn)支持向量分別計(jì)算b的值，然后求平均值，即

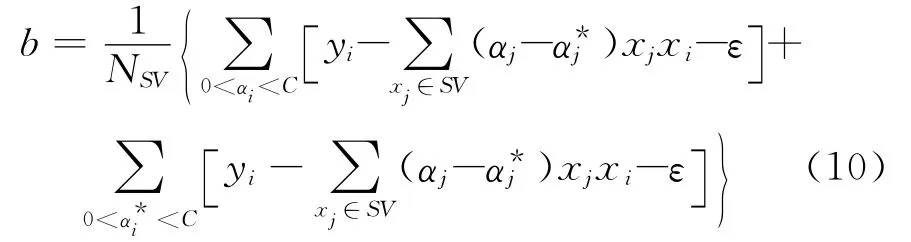
式中，NSV表示標(biāo)準(zhǔn)支持向量的個(gè)數(shù).

最終求得的線性擬合函數(shù)為

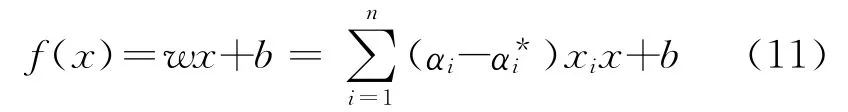
對(duì)于非線性回歸問(wèn)題，首先通過(guò)一個(gè)非線性映射Φ（x）將樣本數(shù)據(jù)映射到某個(gè)高維特征空間中，在高維特征空間中進(jìn)行線性回歸，這樣將原空間中的非線性回歸問(wèn)題轉(zhuǎn)化為高維特征空間中的線性回歸問(wèn)題.為了從原始空間中抽取特征，將原始空間中的樣本映射為高維特征空間中的一個(gè)向量，引入的映射函數(shù)K（xi，xj），稱為核函數(shù)［18］，核函數(shù)是連接低維與高維之間的橋梁.

常用的核函數(shù)有多項(xiàng)式核、S型核、RBF（radial basis function）核 等［19］.本 文 選 擇Gaussian 型RBF［20－21］作為SVM的核函數(shù)，其形式為K（x，x′）＝exp（－‖x－x′‖／2σ2），其中，x′ 為核函數(shù)中心，σ為函數(shù)的寬度參數(shù)，控制了函數(shù)的徑向作用范圍，通過(guò)徑向基函數(shù)實(shí)現(xiàn)了用一元函數(shù)表示多元函數(shù)的目的.

于是，式（5）轉(zhuǎn)化為

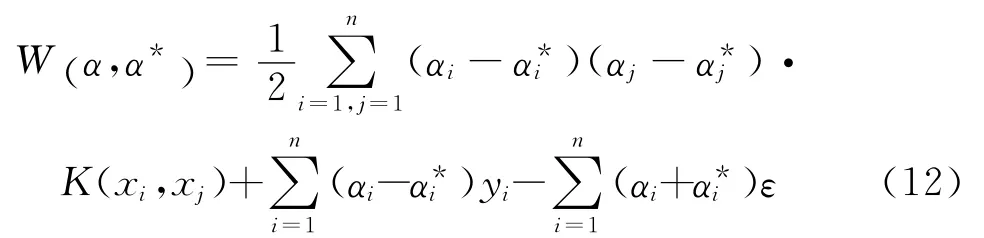
約束條件與線性問(wèn)題相同，這樣就得到非線性擬合函數(shù)的表達(dá)式為

3 樣本訓(xùn)練結(jié)果

以江蘇省某風(fēng)電場(chǎng)2013年1月的10min運(yùn)行間隔數(shù)據(jù)作為初始樣本，選定機(jī)組的額定風(fēng)速為11m／s，按工況條件提取樣本I和II，剔除樣本I，II中的壞點(diǎn)，再進(jìn)行歸一化處理.用SVM、BP 神經(jīng)網(wǎng)絡(luò)分別對(duì)預(yù)處理（DPP）后的樣本和處理前的樣本進(jìn)行訓(xùn)練，選取均方根誤差（RMSE）和平均相對(duì)誤差（MRE）作為訓(xùn)練和預(yù)測(cè)效果的主要判別依據(jù).

均方根誤差

平均相對(duì)誤差

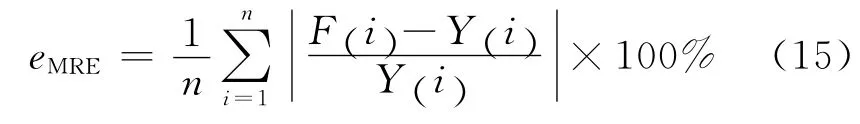
式中，Y（i）和F（i）分別為實(shí)際值和預(yù)測(cè)值.

選定風(fēng)速作為輸入變量，即X＝v，輸出功率作為輸出變量Y＝P，對(duì)樣本I進(jìn)行預(yù)處理后樣本點(diǎn)從3 608個(gè)縮減到了1 831個(gè).由于支持向量的數(shù)目隨著預(yù)設(shè)誤差ε的增大而減小，根據(jù)訓(xùn)練過(guò)程，取ε＝0.001，此時(shí)支持向量數(shù)目較少，數(shù)據(jù)點(diǎn)的逼近精度較高.選用雙線性網(wǎng)格搜索法，對(duì)SVM 參數(shù)σ2和C進(jìn)行優(yōu)選，得到最優(yōu)參數(shù)σ2＝0.328 2，C＝1 028.BP神經(jīng)網(wǎng)絡(luò)采用標(biāo)準(zhǔn)的3層網(wǎng)絡(luò)模式，SVM 和BP神經(jīng)網(wǎng)絡(luò)的輸入層節(jié)點(diǎn)數(shù)均為3，輸出層節(jié)點(diǎn)數(shù)為1，訓(xùn)練得到額定風(fēng)速以下P－v運(yùn)行曲線，結(jié)果如圖3和圖4所示（見(jiàn)下頁(yè)）.

圖3 BP神經(jīng)網(wǎng)絡(luò)算法下P－v 曲線預(yù)測(cè)結(jié)果Fig.3 P－v prediction curves by BP neural network algorithm

圖3和圖4分別為使用BP網(wǎng)絡(luò)和SVM 算法對(duì)處理前和處理后的樣本進(jìn)行訓(xùn)練，并將得到的預(yù)測(cè)曲線與標(biāo)準(zhǔn)風(fēng)功率曲線進(jìn)行對(duì)比，進(jìn)一步計(jì)算得到表1中的預(yù)測(cè)誤差.比較圖3中的BP和DPP－BP曲線以及圖4中的SVM 和DPP－SVM 曲線可以看出，數(shù)據(jù)預(yù)處理后的樣本訓(xùn)練得到的曲線比處理前貼合得更好；比較圖3、圖4和表1可以看出，與BP神經(jīng)網(wǎng)絡(luò)算法相比，運(yùn)用SVM 算法的訓(xùn)練結(jié)果更加靠近標(biāo)準(zhǔn)風(fēng)功率曲線，訓(xùn)練誤差更小并且訓(xùn)練時(shí)間更短.

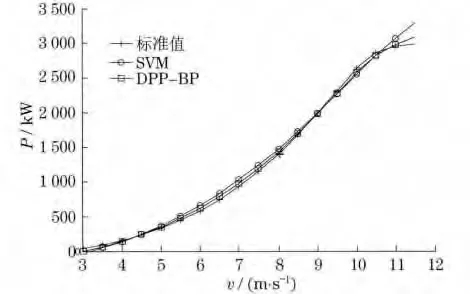
圖4 SVM 算法下P－v 曲線預(yù)測(cè)結(jié)果Fig.4 P－v prediction curves by SVM algorithm

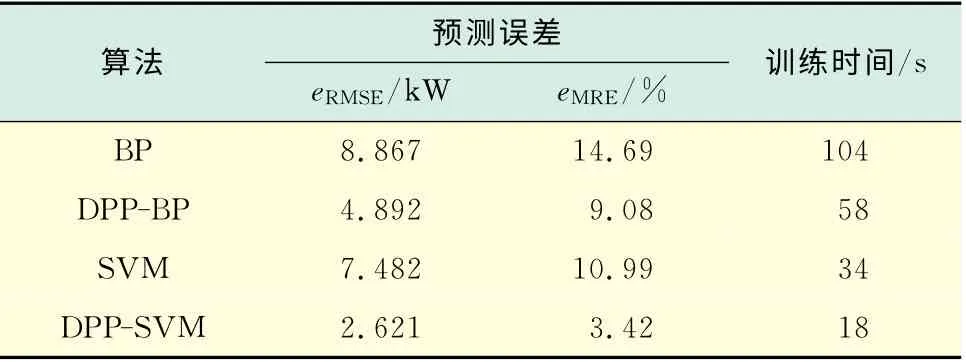
表1 P－v 曲線在不同算法下的預(yù)測(cè)誤差和訓(xùn)練時(shí)間Tab.1 Prediction error and training time of P－v curves by different algorithms

應(yīng)用上述方法，分別通過(guò)樣本I和II訓(xùn)練得到轉(zhuǎn)速－風(fēng)速（ω－v）曲線和槳距角－風(fēng)速（β－v）曲線，剔除壞點(diǎn)后樣本I（ω－v）數(shù)據(jù)點(diǎn)從3 573縮減到1 424個(gè)，樣本II（β－v）數(shù)據(jù)點(diǎn)從2 108縮減到971個(gè)，訓(xùn)練結(jié)果如圖5和圖6所示.

由于ω－v，β－v 標(biāo)準(zhǔn)曲線無(wú)法獲得，選擇訓(xùn)練誤差作為準(zhǔn)確性的判別依據(jù)，表2和表3分別是訓(xùn)練ω－v和β－v曲線得到的訓(xùn)練誤差和訓(xùn)練時(shí)間.

圖5 不同算法下ω－v 曲線預(yù)測(cè)結(jié)果Fig.5 ω－v prediction curves by different algorithms

圖6 不同算法下β－v 曲線預(yù)測(cè)結(jié)果Fig.6 β－v prediction curves by different algorithms

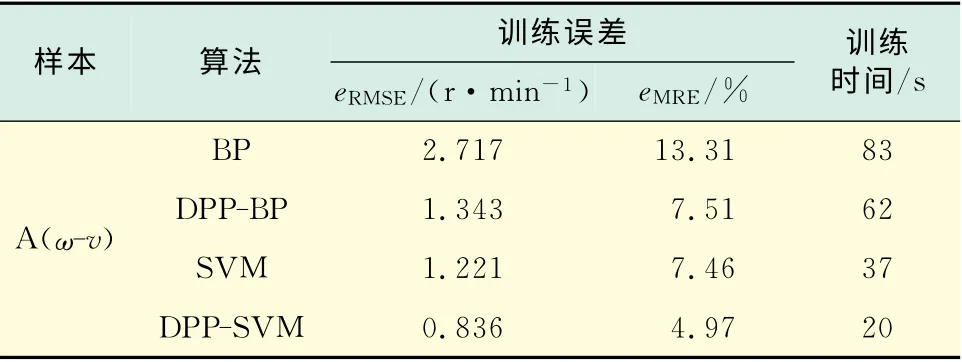
表2 ω－v 曲線在不同算法下的訓(xùn)練誤差和訓(xùn)練時(shí)間Tab.2 Training error and training time ofω－v curve by different algorithms

表3 β－v 曲線在不同算法下的訓(xùn)練誤差和訓(xùn)練時(shí)間Tab.3 Training error and training time ofβ－v curve by different algorithms

比較圖3和圖4可知，訓(xùn)練得到的P－v 曲線與圖1的標(biāo)準(zhǔn)運(yùn)行曲線BC 段的走勢(shì)基本一致；在圖5中，ω－v曲線的風(fēng)速v 在5～8m／s變化時(shí)，轉(zhuǎn)速和風(fēng)速基本符合一次函數(shù)關(guān)系，說(shuō)明在這一工況區(qū)間機(jī)組是嚴(yán)格按照恒葉尖速比規(guī)律運(yùn)行的；在圖6中，β－v曲線的風(fēng)速未超過(guò)額定風(fēng)速時(shí)已經(jīng)開始進(jìn)行變槳操作，風(fēng)速較低時(shí)槳距角變化較慢，隨著風(fēng)速增大，變槳幅度呈現(xiàn)先增大后減小的趨勢(shì).進(jìn)一步比較表1、表2和表3中的誤差和訓(xùn)練時(shí)間，由于計(jì)算訓(xùn)練誤差時(shí)用到的樣本點(diǎn)遠(yuǎn)遠(yuǎn)多于計(jì)算預(yù)測(cè)誤差用到的樣本點(diǎn)，因此，訓(xùn)練誤差普遍大于預(yù)測(cè)誤差.比較可得本文提出的基于數(shù)據(jù)預(yù)處理的支持向量機(jī)算法的預(yù)測(cè)精度和訓(xùn)練精度最好，訓(xùn)練速度最快，并且沒(méi)有出現(xiàn)BP 神經(jīng)網(wǎng)絡(luò)中局部誤差過(guò)大的問(wèn)題，具有明顯的優(yōu)越性.

4 結(jié) 論

充分考慮了并網(wǎng)風(fēng)電機(jī)組的運(yùn)行特性，對(duì)實(shí)測(cè)大樣本進(jìn)行數(shù)據(jù)預(yù)處理，分別使用SVM 和BP神經(jīng)網(wǎng)絡(luò)方法對(duì)修整后的樣本進(jìn)行訓(xùn)練.結(jié)果表明，在非線性曲線擬合方面，基于結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則的SVM 算法致力于尋找全局最優(yōu)解，而基于經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化原則的BP神經(jīng)網(wǎng)絡(luò)算法容易出現(xiàn)局部誤差過(guò)大問(wèn)題.本文提出的基于樣本預(yù)處理方法和SVM算法的非線性擬合方法在預(yù)測(cè)精度和訓(xùn)練速度上都存在明顯優(yōu)勢(shì).由于本方法原理簡(jiǎn)單，易于實(shí)現(xiàn)，在風(fēng)電機(jī)組運(yùn)行特性研究領(lǐng)域具有很強(qiáng)的實(shí)用性.

［1］李辰奇，許昌，楊建川，等.基于CFD 的復(fù)雜地形風(fēng)能分布研究［J］.上海理工大學(xué)學(xué)報(bào)，2013，35（3）：270－274.

［2］Hippert H S，Pedreirea C E，Souza R C.Neural networks for short－term load forecasting：A review and evaluation［J］.IEEE Trans，Power Systems，2001，16（1）：44－54.

［3］Hand M M.Variable－speed wind turbine controller systematic design methodology：a comparison of nonlinear and linear model－based designs［R］.Colorado：National Renewable Energy Laboratory，1999.

［4］Vapnik V N.Statistical learning theory［M］.New York：Wiley，1998.

［5］李盼池，許少華.支持向量機(jī)在模式識(shí)別中的核函數(shù)特性分析［J］.計(jì)算機(jī)工程與設(shè)計(jì)，2005，26（2）：302－304.

［6］周洪利，劉培玉.支持向量機(jī)中的模型選擇研究［J］.信息技術(shù)與信息化，2006（6）：61－63.

［7］王鵬，朱小燕.基于RBF 核的SVM 的模型選擇及其應(yīng)用［J］.計(jì)算機(jī)工程與應(yīng)用，2003，39（24）：72－73.

［8］劉東輝，卞建鵬，付平，等.支持向量機(jī)最優(yōu)參數(shù)選擇的研究［J］.河北科技大學(xué)學(xué)報(bào)，2009，30（1）：58－61.

［9］趙璐華，彭濤.一種有效的SVM 參數(shù)優(yōu)化選擇方法［J］.制造業(yè)自動(dòng)化，2010，32（9）：146－149.

［10］徐海龍，王曉丹，廖勇，等.一種基于PSO 的RBFSVM 模型優(yōu)化新方法［J］.控制與決策，2010，25（3）：367－370.

［11］賀媛媛.基于支持向量機(jī)的電力系統(tǒng)短期負(fù)荷預(yù)測(cè)模型研究［D］.大連：大連理工大學(xué)，2005.

［12］牛東曉，谷志紅，刑棉，等.基于數(shù)據(jù)挖掘的SVM 短期負(fù)荷預(yù)測(cè)方法研究［J］.中國(guó)電機(jī)工程學(xué)報(bào)，2006，26（18）：6－12.

［13］徐勤蘭，樊重俊，張鵬.灰色支持向量機(jī)在機(jī)場(chǎng)吞吐量預(yù)測(cè)中的應(yīng)用［J］.上海理工大學(xué)學(xué)報(bào)，2012，34（4）：347－350.

［14］靳忠偉，陳康民，閆偉，等.基于支持向量機(jī)的中長(zhǎng)期電力負(fù)荷預(yù)測(cè)研究與應(yīng)用［J］.上海理工大學(xué)學(xué)報(bào)，2008，30（2）：129－132.

［15］崔瑜琦.基于最小二乘支持向量機(jī)風(fēng)電機(jī)組的預(yù)測(cè)研究［D］.北京：華北電力大學(xué)，2010.

［16］Gunn S R.Support vector machines for classification and regression ［R］.Southampton：Unicersity of Southampton，1998.

［17］Atthajariyakul S，Leephakpreeda T.Neural computing thermal comfort index for HVAC systems［J］.Energy Conversion and Management，2005，46（15／16）：2553－2565.

［18］謝宏，魏江平，劉鶴立.短期負(fù)荷預(yù)測(cè)中支持向量機(jī)模型的參數(shù)選取和優(yōu)化方法［J］.中國(guó)電機(jī)工程學(xué)報(bào)，2006，26（22）：17－22.

［19］Wendland H.Piecewise polynomial，positive definite and compactly supported radial basis functions of minimal degree［J］.Adv Comput Math，1995，4（1）：389－396.

［20］Wu Z M.Generalized Bochner’s Theorem for radial function［J］.Approximation Theory and its Applications，1997，13（3）：47－57.

［21］Lu Y W，Sundararajan N，Saratchandran P.Performance evaluation of a sequential minimal radial basis function（RBF）neural network learning algorithm［J］.IEEE Trans，Neural Networks，1998，9（2）：308－318.