Mathematica在高等數學實驗中的應用

唐世星，毛羽強，楊光

(1.承德石油高等專科學校，河北 承德 067000;2.承德護理職業學院，河北 承德 067000)

高等數學實驗是當前高等數學教學改革中一項重要內容，目前已經在很多高校中開設了該課程［1-5］。通過高等數學實驗學生學會用數學軟件解決高等數學問題，并讓學生親身體會到數學知識在生產、經營和管理活動中的應用，從而增強他們學習數學和用數學的興趣，培養他們應用數學的能力。同時，也可讓學生領會不做數學理論研究，學好數學基礎知識和基本方法也很重要［6-7］。Mathematica軟件是由Wolfram公司開發的一個功能強大的符號計算系統，它提供了范圍廣泛的數學計算功能，支持在各個領域的人們所需要的各種計算功能，其主要功能包括數學分析、數值計算、動態可視化引擎和文件處理與演示工具［8］。本文將通過典型實例探討Mathematica軟件在高等數學實驗中的應用。

1 Mathematica軟件符號計算功能

在高等數學實驗中，函數的極限、一元函數與多元函數微積分、常微分方程、級數求和、冪級數展開等問題的直接求解均是重要的實驗內容。利用Mathematica軟件的符號運算功能可以直接求解這些問題，并得到該問題的解析解。特別是對于一些特殊的積分問題，Mathematica軟件提供了豐富的特殊函數和數值積分表示方法。下面通過幾個典型例子說明Mathematica軟件的符號計算功能:

在 Notebook 中輸入:Limit［x*Sin［b/x］*(1+a/x)^x，x － ＞ Infinity］，使用 Shift+Enter組合鍵執行上述命令即可得到輸出結果為bea。

例2:求微分方程y″－3y'+2y=cosx的通解。

該方程為常系數線性非齊次微分方程，方程的求解過程很繁瑣，很容易出錯。但是使用Mathematica軟件則很容易求得其通解。

在 Notebook 中輸入:DSolve［y″［x］－3y'［x］+2y［x］==Cos［x］，y［x］，x］，使用 Shift+Enter組合鍵執行上述命令即可得到輸出結果為

2 Mathematica軟件繪圖功能

在高等數學實驗中有很多內容是需要借助圖像來解決的，特別是對于定積分的應用、空間解析幾何中的曲線和曲面。借助直觀的幾何圖像能夠讓學生很容易理解函數的特性，對于高等數學中的一些復合函數的圖像，即使是教師也不容易直接畫出。但是借助于Mathematica軟件強大的繪圖功能，只需簡單的幾行命令就能畫出直觀準確的函數圖像，從而對函數的各種幾何特性更容易理解。

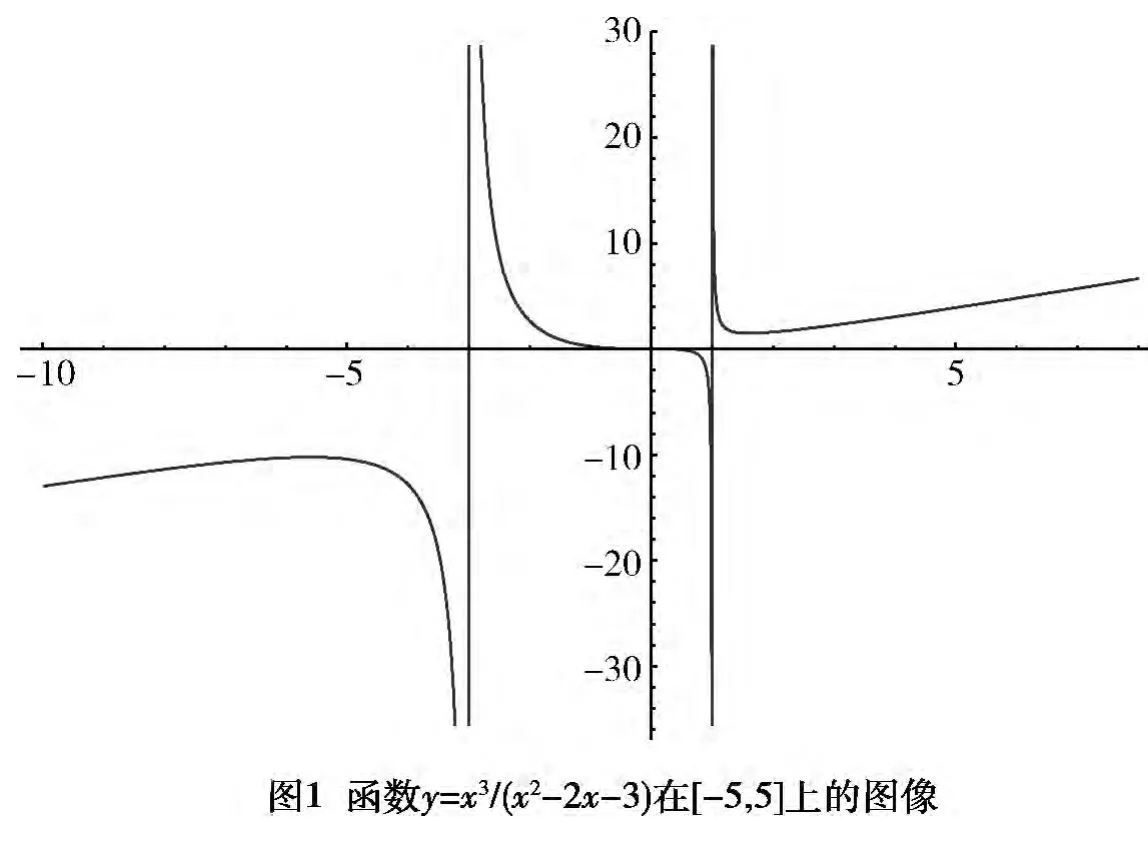
根據高等數學中函數畫圖的一般步驟，該函數的圖像是可以畫出的，但是計算過程較為復雜。使用Mathematica軟件則很容易做出該函數的圖像，在Notebook里輸入命令:Plot［x^3/(x^2－2x－3)，{x，－5，5}］，執行后即可得到如圖1所示的函數圖像。由圖像可以觀察出該函數的單調性、凹凸性及漸近線，其中該函數的斜漸近線在圖像上能夠直觀的觀察出來，但是沒有畫出。由斜漸近線的定義，不難得出該曲線的斜漸近線方程為y=x－2。

3 Mathematica軟件動態可視化功能

在較新版本的Mathematica軟件中提供了更加豐富的動態可視化功能，特別是Manipulate和Animate兩個命令使得交互式操作和可視化功能更加強大，從而為高等數學實驗中有很多內容的動態演示和交互式操作提供了強有力的幫助。通過交互式操作和動態演示使得學生能夠更清晰的看到變化過程，觀察到每一個細節，這樣對高等數學實驗的教學工作大有裨益，同時也增加了學生學數學、用數學的興趣。

例4:某電器廠在對冰箱制冷后斷電測試其制冷效果，t小時后冰箱的溫度為(單位:℃)。問冰箱溫度T關于時間t的變化率是多少?

根據高等數學中導數的相關知識，可以比較容易的得到冰箱溫度T關于時間t的變化率為但是這樣的結果對于理解冰箱溫度關于時間的變化率不夠直觀、明了，下面通過該問題的動態交互式操作功能實現過程來簡要介紹一般的交互式功能實現過程:

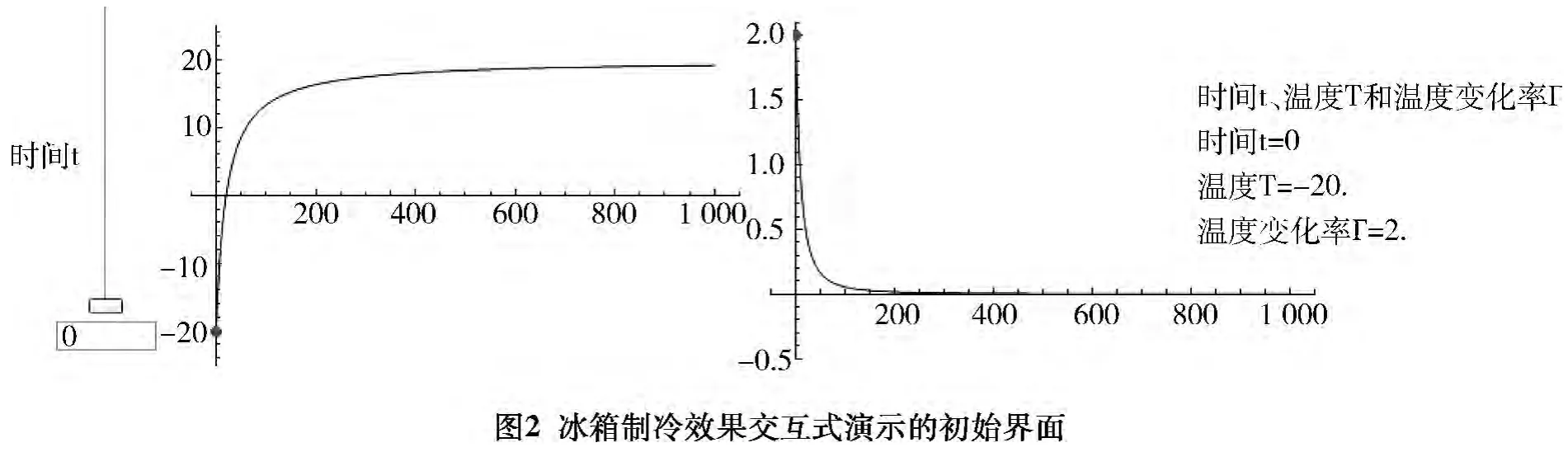
首先:設計界面。根據該問題可以考慮設計四個部件來實現交互式過程:1)時間軸;2)冰箱溫度隨時間的變化圖像;3)冰箱溫度關于時間的變化率圖像;4)時間、冰箱溫度及溫度變化率的動態數字顯示。

其次:根據每一個組件的功能分別設計代碼予以實現，同時通過執行代碼直觀的觀察效果，根據需要進行微調。

本示例的代碼如下:

執行后得到圖2所示的設計界面:

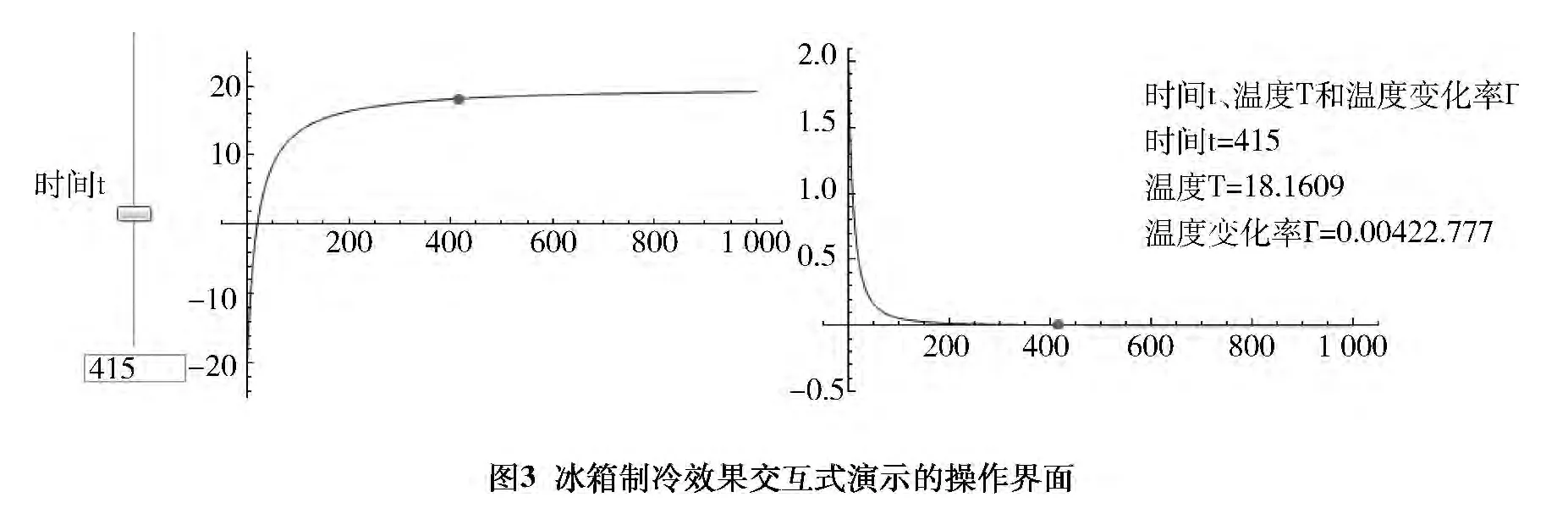
通過點擊右上角的“+”按鈕，可以進行相關的操作，例如粘貼快照、自動運行等，也可以手動調節時間軸，其它三個部件會隨著時間t的變化而變化，充分實現交互式操作功能，可對冰箱制冷效果有一個更為直觀的理解(如圖3所示)。

4 結束語

高等數學實驗對提高學生學習數學的興趣、動手能力和創新能力起著積極的推動作用，能夠有效提高學生分析處理實際問題的能力。通過Mathematica軟件在高等數學實驗中的應用，學生可以充分利用計算機和Mathematica軟件處理運算復雜的工程問題，從而大大簡化了繁瑣的運算過程，提高工作效率，培養了學生的科技創新意識，取得了良好的教學效果。

［1］郭科.數學實驗高等數學分冊［M］.北京:高等教育出版社，2009.

［2］章棟恩，許曉革.高等數學實驗［M］.北京:高等教育出版社，2004.

［3］彭華，吳昶.高等院校的數學實驗課程建設［J］.黑龍江高教研究，2006(141):145－146.

［4］王學會.高等農業院校大學數學實驗課滲透理論教學的實踐與探討［J］.山東社會科學，2011(5):197－198.

［5］黃寬娜.基于信息技術的高等數學實驗教學模式研究［J］.西南師范大學學報(自然科學版)，2011，36(2):210－214.

［6］蕭鐵樹.大學數學實驗(第二版)［M］.北京:高等教育出版社，2006.

［7］唐世星，劉穎華.基于GUI的高等數學實驗教學系統［J］.承德石油高等專科學校學報，2012(3):83－86.

［8］面向高等教育的Mathematica:高等教育解決方案［EB/OL］.http://www.wolfram.com/solutions/education/higher-education/2011－01－18.

［9］楊波.Mathematica與高職高等數學教學的整合研究［J］.高職教育，2012(6):211－213.

［10］艾冬梅.加強數學實驗教學，培養學生應用數學的能力［J］.實驗技術與管理，2007，24(4):25－27.