基于多尺度熵-BP神經網絡的采煤機搖臂齒輪故障診斷
胡 曉,錢沛云,陳曦暉,程 剛
HU Xiao1,QIAN Pei-yun2,CHEN Xi-hui1,CHENG Gang1
(1.中國礦業大學 機電工程學院,徐州 221116;2.上海天地股份有限公司 上海分公司,上海 200021)
0 引言
煤炭是我國的主體能源,隨著采煤機械化的發展,采煤機成為綜采工作面最主要的采煤機械設備。隨著設備的老化和高強度的生產模式,作為采煤機最薄弱部分,搖臂齒輪箱成為了采煤機的故障多發區[1]。為了提高采煤機搖臂運行可靠性,對其進行故障診斷研究有著重要的工程意義。
在目前的故障診斷技術中,因振動信號采集方便,使得振動分析方法比較常見。故障診斷的關鍵就是從機械振動信號中提取特征信息,采集到的振動信號一般是非平穩信號,含有干擾信號和噪聲。為了后期精準的診斷分析,必須在研究過程中對振動信號進行降噪等處理。樣本熵算法是用來刻畫時間序列在單一尺度上的自相似性和復雜性程度,具有抗干擾和抗噪的能力,但是時間序列的復雜度與其在尺度上的特性有著密切的關系,而且考慮到多尺度算法具有高效率、收斂性好和精度較高等優點,在此提出利用多尺度熵算法對齒輪振動信號進行復雜度分析,能有效地提取其中的特征信息[2~4]。最后結合BP神經網絡具有通過學習逼近任意非線性映射的能力,就能有效的對齒輪故障類型進行診斷識別[5~8]。
1 模型建立
1.1 多尺度熵
1.1.1 多尺度演算
對于給定長度為N的時序信號 x1,x2,...,xN,按尺度因子τ 分割成多個長度為τ的數據組,本文取τ=20。然后再利用式(1)求得分割后的每個數據組的平均值,構成新的時間序列,這一過程稱為粗粒化,如圖1所示。


圖1 粗粒化過程
1.1.2 樣本熵定義
樣本熵是2000年由Richman提出的一種與近似熵類似但精度更好的度量時間序列復雜性的方法。其計算方法大致如下:
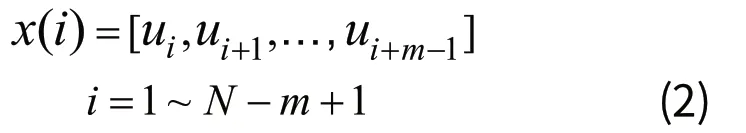
2)定義其中任意兩個樣本 x (i)和 x (j)之間的距離dij:
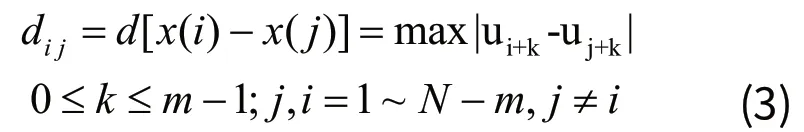
3)引入相似容限t,統計dij<r的個數 Dij(r),求其平均值:

4)當重構數據維數為m 時,計算樣本的平均相似度 φm(r):

5)當重構數據維數為m+1 時,重復步驟2)~5)計算得到,進一步得到φm+1(r);
6)原始時間序列的樣本熵定義為:

當N 為有限數時,上式表示為:

由上式可知樣本熵值SampEn (m,r ,N)與嵌入維數m,相似容限r和數據長度N有關,根據數據長度,嵌入維數m值取值為2,考慮到對信息的保留以及對結果噪聲的敏感性,相似容限r一般取0.1~0.25σ(σ為原始時間序列的標準差),本文取r=0.15σ。
1.2 多尺度熵分析
對每個粗粒序列求樣本熵值,得到τ個粗粒序列的樣本熵值,并把熵值轉化成關于尺度因子的函數,稱之為多尺度熵分析。
多尺度熵定義為時間序列在不同尺度因子下的樣本熵,熵值越大,序列越復雜;熵值越小,序列越簡單,序列自身的相似性越高。多尺度熵曲線反映的是時間序列在不同尺度因子下的自相似性、復雜性以及維數變化時序列產生新模式的能力。因此利用多尺度熵的計算,能有效提取該時間序列的特征信息[4]。
1.3 BP神經網絡
BP神經網絡診斷過程包含訓練過程和應用過程。訓練過程由前向計算過程和誤差反向傳播過程組成,通過訓練使網絡具有聯想記憶和預測能力。應用過程只包含前向計算過程。如圖2所示。

圖2 BP神經網絡診斷過程
2 實驗裝置及數據采集方式
采煤機搖臂齒輪故障診斷識別實驗在采煤機搖臂綜合模擬實驗臺上進行,選用3個加速度傳感器對齒輪振動進行監測,如圖3所示。通過對采煤機搖臂傳動系統第一級傳動齒輪進行更換,模擬出正常、斷齒、少齒和磨損四種齒輪狀態。本文主要對這四種齒輪狀態進行實驗,采集振動信號進行診斷識別分析,確定齒輪故障類型。

圖3 采煤機搖臂試驗臺及傳感器布置
實驗過程中盡量保持四種狀態齒輪工作條件相同,采樣頻率設置為10KHz。采煤機搖臂四種狀態齒輪采集的原始振動信號如圖4所示。

圖4 四種齒輪狀態下振動信號
3 實驗與分析
本實驗測得的采煤機搖臂齒輪振動信號共有四種類型,分別為正常、斷齒、少齒和磨損四種齒輪狀態。將采集到的振動信號每2048個數據點分割為一個樣本,每種齒輪狀態類型截取100個樣本。由于采用振動信號1~20尺度的樣本熵作為信號特征,并且最終需將信號準確分成4類,即輸入層有20個節點,輸出層有4個節點。
針對單隱含層網絡,其在快速性和可靠性方面存在一定缺陷。為了提高網絡的診斷精度,對隱含層節點數進行優化處理。
一般來說網絡隱含層節點數太少,網絡將不能建立復雜的映射關系;節點數過多,網絡學習時間過長。因此,本文選取刪除法,先采用一個較大的隱含層節點數,若網絡輸出誤差不符合設定的要求,則逐步刪除隱含層節點,直至合適為止。下面對隱藏層節點數進行優化。
首先,隱含層節點數l 的初始確定按經驗公式l=(0.5~1.5)m,本文選取:l=1.5×20=30,然后采用刪除法,逐步刪除節點,根據實驗測得的分類誤差率選擇最優值,如圖5所示。

圖5 誤差率變化
由圖5可知,當隱含層節點數l=23 時,網絡的預測精度最高,選取 l=23 為隱含層節點數最優值。BP神經網絡的網絡結構選定為20-23-4。
然后將經過多尺度熵計算處理后的振動信號樣本進行隨機混合,從混合的樣本中隨機抽取75%的數據作為訓練樣本,剩下的25%作為驗證樣本。最后利用訓練后BP神經網絡對驗證樣本進行分類。
圖6為實際故障類型與預測對比圖,由此我們可以直觀的看到對故障類型的識別情況,其中“△”表示預測的齒輪類型,“*”表示實際的齒輪類型,“△”和“*”重合表示齒輪類型識別正確,單獨出現的“△”表示齒輪類型識別錯誤。

圖6 實際故障類型與預測對比圖
統計實驗對測試樣本的故障識別率如表1所示。

表1 齒輪故障類型識別率
由表1可知,實驗中對于四類齒輪類型的識別率達到84.0%以上,說明該方法能夠有效的對采煤機搖臂齒輪故障診斷識別。
4 結論
實驗結果表明:采用多尺度熵結合優化后的BP神經網絡的搖臂齒輪故障診斷方法,對于齒輪故障類型的識別率達到84.0%以上,特別是對正常齒輪的識別率達到了95.65%,減少了出現誤診斷的幾率,因此該方法對采煤機搖臂齒輪的故障類型能夠有效地診斷識別。未來將進一步研究對神經網絡優化處理,提高故障診斷識別效率,加強在故障實時診斷、預測方面的應用。
[1]周久華,米林.采煤機搖臂齒輪箱故障與可靠性分析[J].內蒙古科技與經濟,2011,(14):107-108,110.
[2]林庭毅.基于多尺度方均根、多尺度熵、費雪法與倒傳遞網絡之軸承錯誤診斷系統[D].臺北:國立臺灣師范大學,2012:8-12.
[3]鄭近德,程軍圣,楊宇.基于多尺度熵的滾動軸承故障診斷方法[J].湖南大學學報(自然科學版),2012,39(5):38-41.
[4]M.Costa,A.L.Goldberger and C.K.Peng.Multi-scale Entropy Analysis of Complex Physiologic Time Series[J].Physical Review Letters,2002,6(89):1-4.
[5]史峰,王小川,郁磊,等.MATLAB神經網絡30個案例分析[M].北京:北京航空航天大學出版社,2010:1-10.
[6]李萍,曾令可,稅安澤,金雪莉,劉艷春,王慧.基于MATLAB的BP神經網絡預測系統的設計[J].計算機應用與軟件,2008,25(4):149-151.
[7]呂硯山,趙正琦.BP神經網絡的優化及應用研究[J].北京化工大學學報(自然科學版),2001,28(1):67-69.
[8]張山,何建農.BP神經網絡的優化算法研究[J].計算機與現代化,2009,(1):73-75.

