求極限的常用方法與技巧

金世國 王廣江

（河南廣播電視大學(xué)，河南 鄭州 450008）

極限是高等數(shù)學(xué)的基本研究工具， 高等數(shù)學(xué)中的一些重要概念——連續(xù)性、導(dǎo)數(shù)、微分、定積分、級數(shù)等都是建立在極限的基礎(chǔ)上。 本文將介紹求極限的常用方法與技巧。

1 利用極限的四則運算法則

利用極限四則運算法則時，需注意以下兩點：

（1）保證各項極限均存在，對商的運算法則還要確保分母極限不為零。

例1：求下列極限，

2 利用兩個重要極限

兩個重要極限的一般形式為：

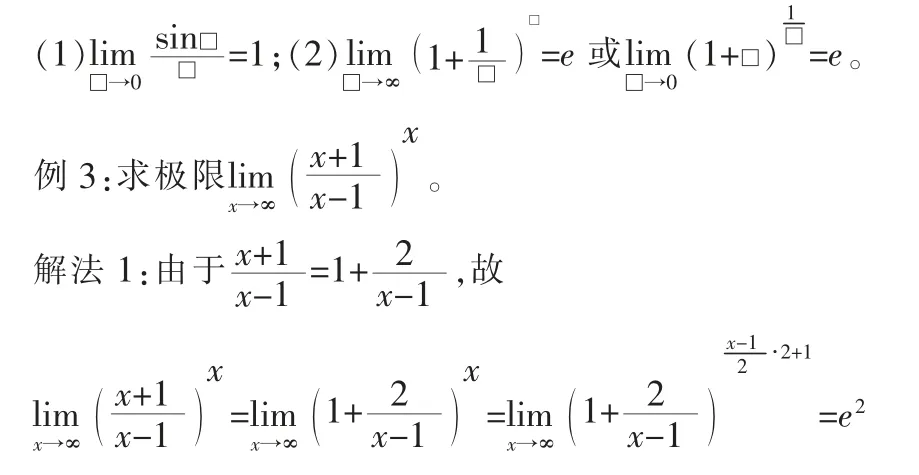
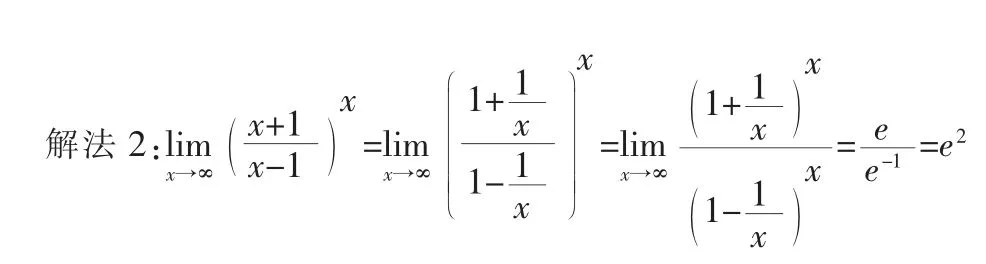
3 利用極限存在準(zhǔn)則

（1）夾逼準(zhǔn)則

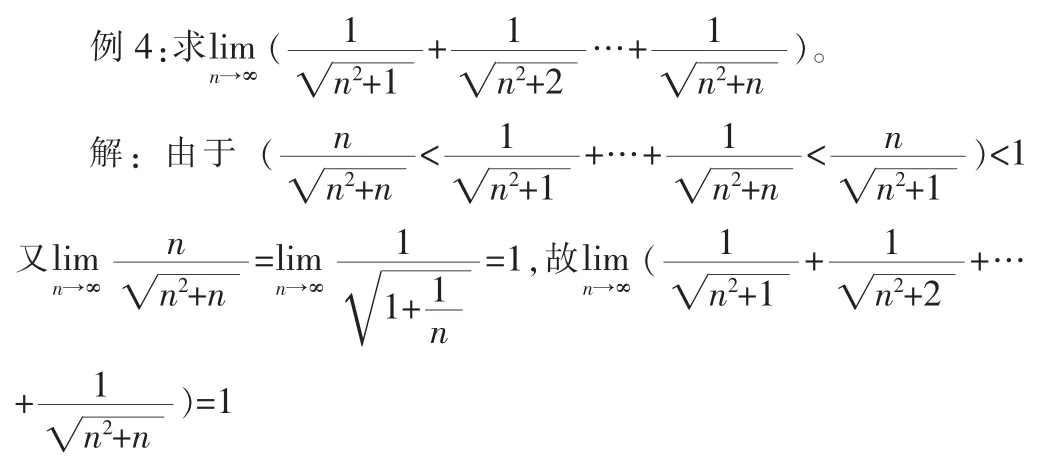
（2）數(shù)列的單調(diào)有界收斂準(zhǔn)則

4 利用無窮小量的性質(zhì)

有限個無窮小量的和、差、積仍是無窮小量；有界量與無窮小量之積仍是無窮小量。

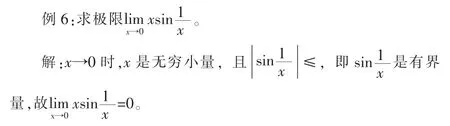
5 利用等價無窮小替換定理

利用等價無窮小替換定理求極限，必須對分子、分母的整體進行代換，或者對分子、分母的部分因式進行代換，對分子、分母中由“+”、“”相連接的各部分不能分別作代換。

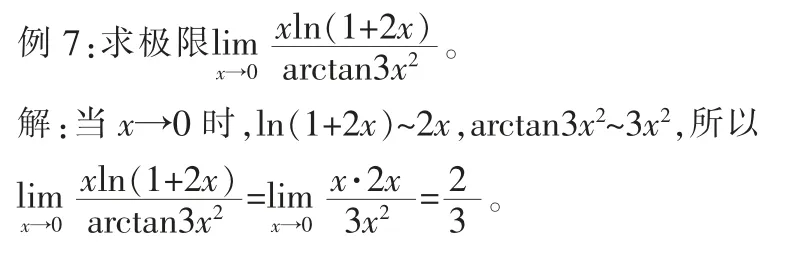
6 利用初等函數(shù)在其定義區(qū)間內(nèi)的連續(xù)性

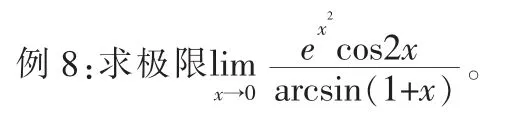
7 利用洛必達法則

解：該極限是1∞型未定式，可先取對數(shù)，然后按照上例方法進行求解。

8 利用泰勒公式求極限

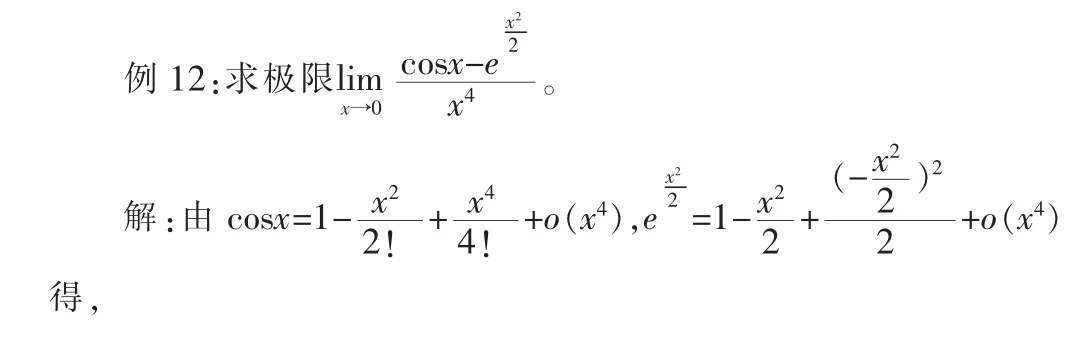
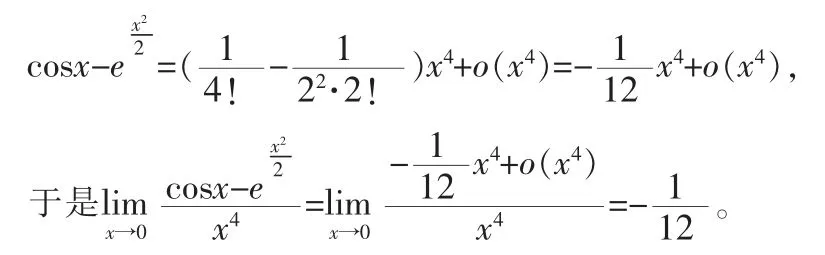
9 利用定積分的定義

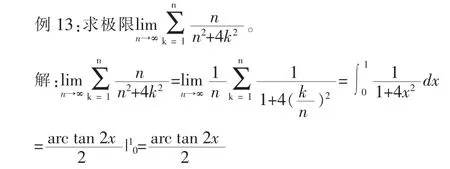
10 利用積分中值定理

上面對求極限的方法做了比較全面的總結(jié)，由此可見，極限方法靈活多樣，要想掌握各種方法，必須多做多練。

[1]同濟大學(xué)數(shù)學(xué)系.高等數(shù)學(xué)（第六版）[M].北京：高等教育出版社，2007.

[2]華東師范大學(xué)數(shù)學(xué)系.數(shù)學(xué)分析（第四版）[M].北京：高等教育出版社，2011.

[3]張靜茹.高等數(shù)學(xué)[M].南京：江蘇教育出版社，2012.