破解實質蘊涵怪論之謎

●李鐵強

(武警學院部隊管理系，河北廊坊 065000)

(本欄責任編輯、校對 李獻惠)

在經典命題演算系統中，出現了四個讓人費解的實質蘊涵怪論:(1)p→(q→p)。即真命題被任何命題所蘊涵。(2)～p→(p→q)。即假命題蘊涵任何命題。(3)(p→q)∨(q→p)。即任一兩個命題之間都有蘊涵關系。(4)(p→q)∨(p→～q)。即任意命題p不是蘊涵任意命題q，就是蘊涵～q。

對于為什么會出現這些怪論又如何消除它們，是邏輯學研究的一項重要任務。要完成這一任務，我們必須仔細審視如下對于實質蘊涵理論一般性評價的真實性:“實質蘊涵抽象、概括出了語言中‘如果，則’這類聯結詞的共性，在對‘如果，則’的各種解釋中是最弱的，因而具有普遍適用性和簡單性，而這種普適性和簡單性是邏輯的本質要求”［1］，并由此出發，探討消除實質蘊涵怪論的途徑。

一、實質蘊涵經典含義的內在矛盾性

把真值和真值函項的概念引入邏輯，是現代命題邏輯取得實質性進步的關鍵環節。但是，在用“→”來表示的實質蘊涵以概括性地把握“如果…那么…”的條件句時，“p→q”的真值與“如果p那么q”這種形式的條件句的真假是否是一致的?

如果我們把討論問題的范圍限定在原子命題的范圍之內，那么非常明顯的是，命題p的真值與命題p的真假是完全一致的。但是，如果我們把討論問題的范圍限定在除了～p之外的復合命題的范圍之內，那么情況就會變得復雜起來。事實上，自古希臘提出蘊涵概念開始，將“如果p那么q”的真假與“p→q”的真值就混淆起來。我們以實質蘊涵的首倡者斐洛為例。他認為“一個條件命題是正確的，不是前件真，后件假。”這就是說，一個真的充分條件假言命題可以用三種方式得到:(1)以真的前件開始并且以真的后件結束。例如:“如果這是白天，那么這是亮的。”(2)以假的前件開始并且以假的后件結束。例如:“如果地球會飛，那么地球有翼。”(3)以假的前件開始以真的后件結束。例如:“如果地球會飛，那么地球存在。另外當且僅當前件真而后件假時，條件命題才是假的。例如:“如果是白天，那么是黑夜。”［2］從斐洛對蘊涵命題的定義和他舉例的方式來看，他的核心思想是，條件命題的真值與條件命題的真假是完全一致的。這種思想深刻地影響了從皮爾士、弗雷澤，到羅素、維特根斯坦等眾多的現代邏輯學家，使他們普遍繼承并堅持這一觀點，所以，他們才絲毫不懷疑斐洛所例示的條件命題的真實性，進而構造出不計其數且認為是正確的類似命題。此種對條件命題的理解所導致的最為致命的后果是，一個條件命題的真假可以由前件和后件的一組真值來確定。［3］而這一點卻給條件命題的描述引入不可避免的矛盾:用前件和后件的一組賦值的真正目的是確定條件命題的真假。但如果是這樣的話，我們將無法確定一個條件命題的真假。以“如果兩物體產生摩擦，那么地面會濕”這個命題為例，在某種場景之下，前件和后件都是真，依據斐洛的觀點，這個條件命題是真的;但是，這個命題在另外的場景之下，會出現前件真而后件假的情形，這樣依據斐洛的觀點，這個條件命題是假的。所以，如果斐洛的觀點是正確的話，那么我們不得不得出這樣的結論，條件命題的真假因時而異、因地而異!

這樣的結論與我們通常要建立“如果p那么q”形式的條件命題、特別是用這種形式建立科學理論的目的是背道而馳的。建立條件命題的目的是要尋求前件和后件之間的必然聯系，通過利用這種聯系，我們可以有效地預期未來或者對事物的運動變化和發展實施有效的控制，以達到認識世界和改造世界的目的。在通常情況下，條件命題，如“如果兩物體產生摩擦，那么會產生熱”，并不對前件和后件的真假做出具體的承諾，它只是承諾:當兩物體確實產生摩擦時，一定會產生熱;當兩物體沒有產生摩擦時，它可能會產生熱也可能不產生熱;不會發生這樣的情況，當兩物體產生摩擦時，沒有熱量產生。這樣的承諾與墨子學派的經典描述:“有之必然，無之未必不然”完全吻合，而與實質蘊涵的經典描述不完全相符。

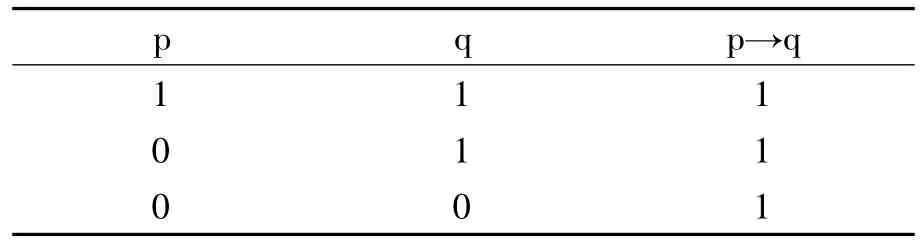
國內普通邏輯教材中充分條件假言命題的定義，由于采用墨家學派的經典描述，因而與科學中條件命題的使用相符合;它把充分條件假言命題之真與真值在不自覺間有效區分開來，即前件和后件的一組確定真值賦值不足以確定充分條件命題的真假，其真必須在綜合地考察前件和后件的全部賦值對后才能確定:它既要考察前件p與后件q在不同的情形下是否會出現賦值對〈1，1〉與〈1，0〉以確定是否滿足“有之必然”，也要考察在不同的情況下是否會出現〈0，1〉與〈0，0〉以確定是否滿足“無之未必不然”。當然作為邏輯的抽象，當我們用符號表示充分條件假言命題的變項和常項后，一個真的充分條件假言命題的真值情況就可以用真值表(如下)來表示。這個真值表的地位極其重要。因為就是依據這個真值表我們才得到充分條件假言命題推理的基本規則和兩個基本推理有效形式:肯定前件式和否定后件式。在此我們應特別注意其基本有效式的建立過程(以肯定前件式為例):假定“如果p那么q”是真的，p和 q的真值有三種可能:〈1，1〉、〈0，1〉和〈0，0〉，這清楚地表明，一個真充分條件假言命題是不能斷定前件與后件具體真值情況的;當第二個前提斷定了前件真的情況下，我們才從這三行真值中斷定，只有第一行才滿足“如果p那么q”和p都是真，所以，q必真。

p q p→q 1 1 1 0 1 1 0 0 1

既然在建立基本有效推理式的時候，從假定“如果p那么q”是真的不能具體斷定前件和后件的真值，那么我們有什么樣的理由在知道前件和后件的一組真值組合后就斷定“如果p那么q”是真或假的呢?即使在這種情況下我們有充分的理由斷定“如果p那么q”的真值，但有什么確切的理由說其真值與其真假是一致的呢?實質蘊涵理論恰恰做出了這樣的斷定。這種把真值與真假視為等同的觀點導致了實質蘊涵的內在矛盾性:一方面，當這種理論建立基本推理有效式時默認了前面的真值表，即從“p→q”是真的出發，只能陳列p和q的各種可能的真值組合，而不能具體斷定前件和后件的真值;但另一方面，當p和q的某種真值組合確立后，這種理論卻不僅立即斷定“p→q”的真值，也同時斷定了“p→q”的真假，并以此為依據構造出眾多的與人們的直觀相違背的條件命題。

二、產生實質蘊涵怪論的原因

當邏輯學家用真值函項理論刻畫實質蘊涵以及整個命題邏輯時，他們都沒有真誠地、科學地對待真值函項這個概念，進而導致實質蘊涵的內在矛盾性;這種矛盾性的進一步后果是實質蘊涵的多樣化，而這一點正是產生實質蘊涵怪論的原因。

既然實質蘊涵理論是用函數理論來刻畫的，那么，用函數做類比既是恰當的也是有益的。我們的問題是:在什么情況下，函數f(x)和g(x)兩者相等;又在什么情況下它們不相等呢?用標準的數學語言來說其答案非常簡單:f(x)=g(x)，當且僅當對于x的任意賦值 xi，f(xi)=g(xi);f(x)≠g(x)，當且僅當存在著賦值xi，使得f(xi)≠g(xi)，而不管有多少情況xj，使f(xj)=g(xj)。數學家乃至學習函數的學生，從來沒有把一個點或幾個點看作曲線或曲面，因為有無數條曲線或曲面會通過一個或幾個點，但當經典實質蘊涵理論把復合命題的真值充當其真假時，恰恰是用一個或幾個點來代替曲線或曲面。于是，多種實質蘊涵就出現了。

當且僅當p與q的真值組合至少有一種不可能實現時，這種情況下的實質蘊涵“p→q”是限定賦值實質蘊涵。事實上，日本學者石黑滿雖然沒有提出限定賦值實質蘊涵的概念，但從本質上講，他已經提及缺行真值表，并提出相應的推理規則［4］。限定賦值實質蘊涵包括單賦值實質蘊涵(共四種)、二賦值實質蘊涵(共六種)、三賦值實質蘊涵(共四種)和四賦值實質蘊涵(一種)。其中，單賦值實質蘊涵就是斐洛所舉實例所理解的實質蘊涵，這相當于把一個點看作曲線或曲面，或者把函數自變量和因變量的一組確定的值看作函數本身。以此方式理解而得的實質蘊涵導致兩個不良后果:一是它無法與許多其它邏輯常項所構成的單賦值真值函項進行有效區分。如在單賦值〈1，1〉的情況下，p→q 與 p∧q、p∨q、p←q及p?q的真值都為1，這樣一來，幾個真值形式就無法區別開來;二是以單賦值的實質蘊涵的有效推理規則與充分條件假言推理規則不完全相同。仍以單賦值〈1，1〉情況為例，以p→q為大前提的推理規則有兩條，即肯定p可以肯定q和肯定q可以肯定p。但這樣一來，推理有效式將得到極大地擴張，然而其存在的合理性卻存在疑問。

當然，這兩個后果也體現在其它不同賦值數量的實質蘊涵當中。但各種實質蘊涵的類型是否有實際的意義及其深入研究不是本文的目的，在此我們只要證明“→”有不同的意義就足夠了。事實上，前件實質蘊涵后件不同種類的存在可以從形式上得到枚舉證明。p∨～p→q∨～q和p∧～p→q∧～q是單賦值實質蘊涵;p→p和p→～p是二賦值實質蘊涵;p∧q→p和p→p∨q是三賦值實質蘊涵中充分實質蘊涵;p∧q→～p和p∨q→p是全賦值實質蘊涵。由此我們可以得出這樣的結論:當邏輯學用符號“→”做出統一的處理后，不但沒有揭示出“如果…那么…”不同用法的共同涵義，反而將其差異和邏輯特性掩蓋起來了。正如美國學者科庇所指出的:“→”這個符號“不應被看做表達了‘如果…那么…’或者蘊涵關系的含義，而應看做用‘如果…那么…’這一短語表示的各種不同的蘊涵所共有的局部因素的符號化。”［5］

正是經典實質蘊涵理論把真值與真假等同起來的觀點所導致的實質蘊涵的多樣性，為我們揭示產生實質蘊涵怪論的根源打開了大門。因為，由此我們可以得出一個重要的結論:在以真值函項理論為基礎的有效推理形式中，“→”的每一次出現往往代表不同的實質蘊涵。

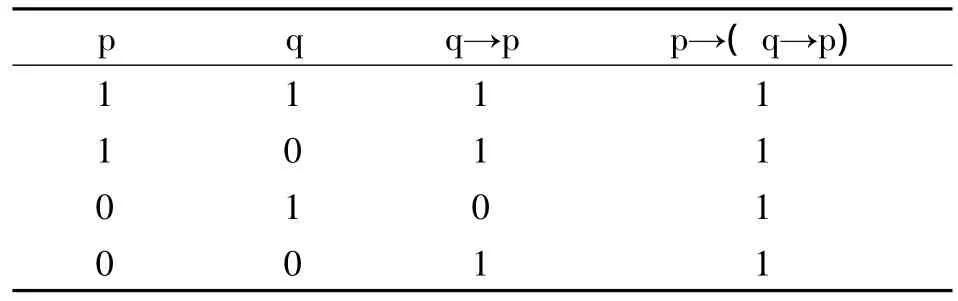
我們以文章開頭所列出的⑴為例。⑴可以表述為:“如果一個陳述是真的，那么它被任何一個陳述所蘊涵”(如，由于“地球是圓的”是真的，可以推出“現任美國總統是奧巴馬蘊涵地球是圓的”)。要說明為什么會出現這樣的怪論，我們只需看這一推理的真理形式中“→”兩次出現的語義是否相同即可。在⑴的真值表中(如下)，我們不難發現:第一，p與q→p的真值組合只有〈1，1〉、〈0，1〉和〈0，0〉三種，但沒有〈1，0〉的真值組合，這說明推理的前提p是結論q→p的充分條件;但是，第二，在結論中的q→p，q與 p的真值組合卻有〈1，1〉、〈0，1〉、〈0，0〉和〈1，0〉四種，是四賦值實質蘊涵，其中q不是p的充分條件。

p q q→p p→(q→p)1 1 1 1 1 0 1 1 0 1 0 1 0 0 1 1

所以，我們可以得出一個重要的結論:在以真值函項理論為基礎的有效推理形式中，“→”的每一次出現往往代表不同的實質蘊涵。一句話，由于把復合命題的真值與復合命題的真假等同起來，導致實質蘊涵理論沒有科學地對待真值函項概念而產生多種多樣的實質蘊涵，由此使實質蘊涵怪論的產生成為必然。

三、消除實質蘊涵怪論的形式途徑

既然我們已經知道實質蘊涵怪論是如何產生的，那么就有可能尋找到某種途徑，通過它我們可以有效消除實質蘊涵怪論。當然，這樣的途徑有語義途徑和形式途徑之別。語義途徑即通過真值方法以判明命題推理形式中“→”在前提中的每一次出現保證為充分實質蘊涵的條件下，其后續的每一次出現是否為充分實質蘊涵，并進而判明命題推理形式是否為實質蘊涵怪論;如果是，則在命題推理系統中取消其定理的地位;如果不是，則保留它，將它視為命題推理系統中的定理。語義途徑從實質上講，是一種對實質蘊涵進行語義限制的方法，以此來消除實質蘊涵怪論。應該說語義途徑只是一種理論上的能行途徑，但由于可以被稱為定理者不計其數，所以不可能通過這種途徑完成此項任務。這迫使我們不得不把考察的視野轉向形式途徑。

科庇提供了由9條推理規則、10條置換規則、(加強)條件證明規則和間接證明規則所構成的命題演算系統。［5］現在我們就以此系統為對象，尋求有效消除實質蘊涵怪論的形式途徑。

綜觀前述推理⑴-⑷，在科庇提供的命題演算系統內如果沒有推理規則中的加法規則“p，∴p∨q”(即∨引入規則)，⑴-⑷都不能得到有效證明;相反，有了加法規則，它們都可以得到簡易而有效的證明。但就是這條規則的地位是十分可疑:它不僅在實際的思維過程中很少得到應用，而且就是借助于它的存在和使用，⑴-⑷才在命題演算中得以產生;更為重要的是，如果我們承認，說推理能夠有效進行下去是建立在假定了前提為真的情況下，那么，在假定p的情況之下，所能得出的確切結論是p∨q的真值為真，而不是p∨q的真，這樣一來，我們即使能合邏輯地推出～p→q(或～q→p)的真值為真，卻無法推出～p→q(或～q→p)的真，否則，就會犯用真值函項的某個真值來取代真值函項真的錯誤。如果這一結論是真實的，那么如下結論就是正確的:取消加法規則在推理規則中的合法地位就可以消除一切實質蘊涵怪論。另外還有一個強有力的理由來消除加法規則。為了保證推理的有效性，謂詞演算系統中的存在例示和全稱概括兩個規則都對變項是否為自由出現有所限定，而命題演算系統中的加法規則卻對變項q的出現沒有任何限定，其結果一是結論中出現了在前提中沒有出現過、可以作任意解釋的同時可能與實際思維過程毫不相關的變項，二就是實質蘊涵怪論的產生。

必須承認，我在這里只是提供了消除實質蘊涵怪論的一種可能途徑。這與其說是提供了一種確切的形式方法，倒不如說是提出了一系列有待研究的問題:消除加法規則在科庇命題演算系統內真的能夠消除一切命題推理反例和實質蘊涵怪論嗎?如果說不能，那么是否存在著其它的途徑?如果說能，那么在自然演算SN系統如何消除它們?是否在公理演算系統如弗雷澤系統、丘奇、希爾伯特-阿克曼系統中重新考察其設定公理的合理性(不管怎樣，在這些系統中要么以實質蘊涵怪論要么以加法規則為其有效公理)呢?進一步地，當我們實現了這一目標之后，那些為克服實質蘊涵怪論而建立起來的其它系統(如嚴格蘊涵理論等)是否還有存在的必要呢?在消除了實質蘊涵怪論之后，命題邏輯系統還是完備的嗎?這些問題，我并沒有找到確切的解決方法和途徑，也超出了本文討論的范圍。現在把它們提出來供廣大同仁深入探討。

［1］陳波．邏輯哲學導論［M］．北京：中國人民大學出版社，2000：117．

［2］馬玉珂．西方邏輯史［M］．北京：中國人民大學出版社，1985：258．

［3］斯蒂芬·里德．對邏輯的思考［M］．遼寧：遼寧教育出版社，1988：82．

［4］末木剛博．邏輯學——知識的基礎［M］．北京：中國人民大學出版社，1984：144-145．

［5］I·M·科庇．符號邏輯［M］．北京：北京大學出版社，1988：43-81，25．