單脈沖作用下在軌攔截器覆蓋范圍研究
武健,劉新學,舒健生,李亞雄,閆建崢
(1.第二炮兵工程大學906教研室,陜西西安710025;2.中國人民解放軍96251部隊,河南洛陽471003)
0 引言
軌道機動是動能型在軌攔截器對目標航天器實施攔截作戰的前提,脈沖軌道機動在工程上易于實現,是各種軌道機動設計的基礎[1-2]。為保證機動軌道設計和優化的可行性,在脈沖軌道機動設計與優化前,應該考慮目標航天器是否在在軌攔截器覆蓋范圍內。
文獻[2]研究了在衛星軌道上任意一點施加大小固定、方向任意的脈沖后生成軌道的可達區域。文獻[3]考慮脈沖幅值較小、生成軌道為橢圓軌道的情況,對初始軌道上任意點施加平面內幅值固定、方向任意的脈沖后衛星的機動范圍進行了研究,所得結論適用于初始軌道為圓軌道和小偏心率橢圓軌道的情況。文獻[4]推導了施加脈沖后生成軌道的運行規律,提出了利用優化理論確定衛星可達范圍邊界的方法,可用于初始偏心率較大的橢圓軌道。文獻[5]利用包絡線的方法確定了衛星在軌道平面內的可達范圍。目前,這些理論研究大都集中于平面脈沖作用下衛星可達范圍的確定[6-7],但對任意方向單脈沖作用下衛星的可達范圍研究較少。
本文圍繞單脈沖作用下在軌攔截器覆蓋范圍展開研究,將初始軌道分為圓軌道和橢圓軌道,研究了單脈沖作用下在軌攔截器覆蓋范圍及描述形式。
1 模型假設與坐標系定義
本文研究中作如下假設:
(1)地球為均勻圓球,半徑Rc=6 371 km;
(2)只考慮地球引力,忽略其他攝動力的影響;
(3)脈沖施加過程瞬間完成,忽略脈沖施加過程中在軌攔截器位置的變化;
(4)在軌攔截器提供的脈沖幅值較小,可提供大小不超過Δvmax、方向任意的脈沖。
本文研究主要在近焦點坐標系下,同時為了數學描述簡捷,設計了一種近焦點坐標系球面坐標表示形式。
(1)近焦點坐標系
以軌道焦點為坐標原點,xy平面為軌道平面且x軸從焦點指向近地點,z軸與角動量方向一致,y軸與x軸和z軸構成右手正交坐標系[8]。
(2)近焦點坐標系的球面坐標描述形式
如圖1所示,定義近焦點坐標的球面坐標形式為(ρ,φ,θ),ρ為某矢量 T 的模;φ 為矢量 T 與其在xOy投影T'夾角;θ為T'與Ox軸夾角。
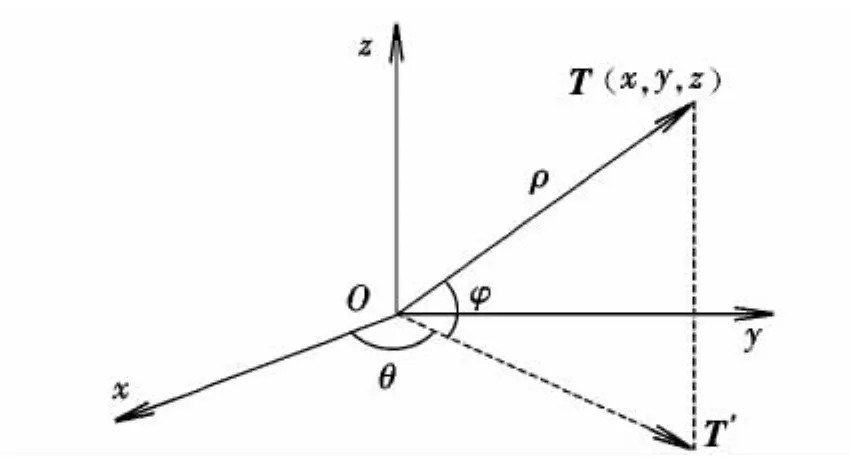
圖1 近焦點坐標系的球面坐標形式Fig.1 Spherical coordinate of near focus coordinate system
球面坐標與直角坐標的轉化關系為:
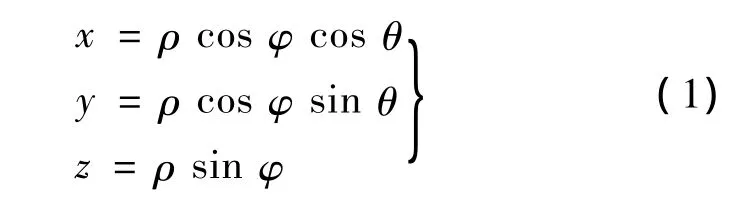
2 圓軌道在軌攔截器覆蓋能力
脈沖Δv可分解為在軌道面內的脈沖ΔvR及垂直軌道面方向的脈沖ΔvW,且滿足:
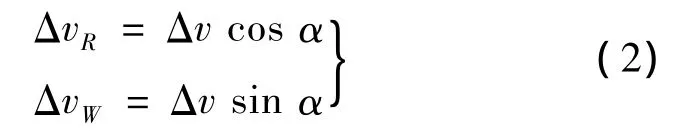
式中,α為脈沖矢量與其在軌道面的投影夾角。
2.1 平面脈沖作用下在軌攔截器覆蓋范圍
平面脈沖ΔvR作用下,利用活力公式推導出脈沖施加前后在軌攔截器的半長軸 a0和 af,具體為[9]:
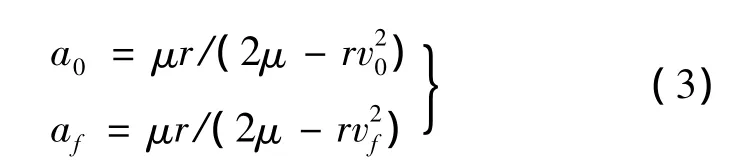
式中,μ為地球引力常數,r為脈沖施加時刻在軌攔截器的地心距;v0,vf為脈沖施加前后在軌攔截器的速度大小。vf計算如下:
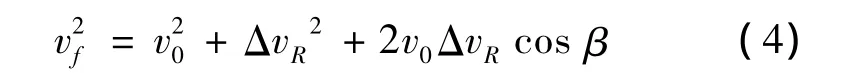
式中,β為脈沖矢量ΔvR與速度矢量v0的夾角。
脈沖施加前后在軌攔截器半長軸改變量為:
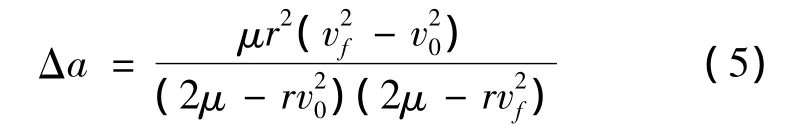
分析可知,Δa為vf的單調遞增函數,當β=0且ΔvR=Δvmax時,半長軸增加最大;當β=π且ΔvR=Δvmax時,半長軸減少最大。由于圓軌道的特性(軌道上各點的地心距、速度大小都相等),則在軌道上每一點施加大小相同、方向與該點速度方向一致(相反)的速度脈沖后,在軌攔截器生成軌道的地心距最大值(最小值)相等。初始軌道為圓形軌道時,平面單脈沖作用下在軌攔截器覆蓋范圍為一圓環,用球面坐標描述為:
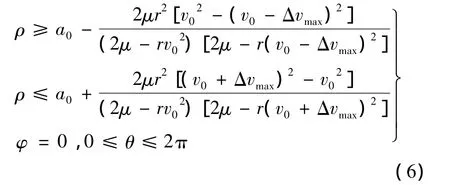
2.2 垂直軌道面脈沖作用下在軌攔截器覆蓋范圍
在垂直軌道面脈沖ΔvW作用下,軌道半長軸的變化Δa及軌道傾角變化Δi計算公式為:
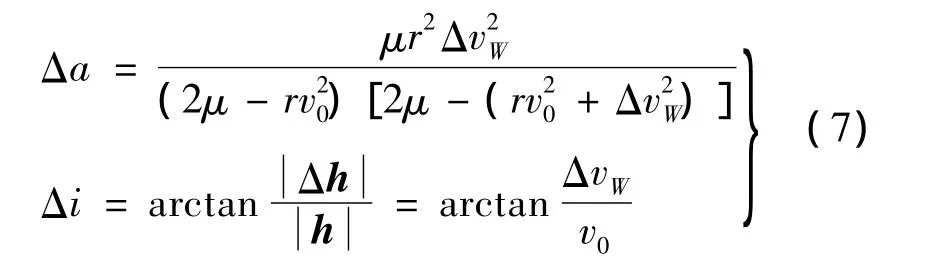
式中,h為角動量;Δh=r×ΔvW,為角動量改變量。
由于圓軌道的特征,在任意點施加方向、大小相同的垂直軌道面脈沖,在軌攔截器生成軌道地心距最大值(最小值)相等,垂直軌道面脈沖引起軌道傾角變化且大小相同。因此,垂直軌道面脈沖作用時,在軌攔截器覆蓋范圍為一曲面繞z軸旋轉形成的區域,用球面坐標描述如下:
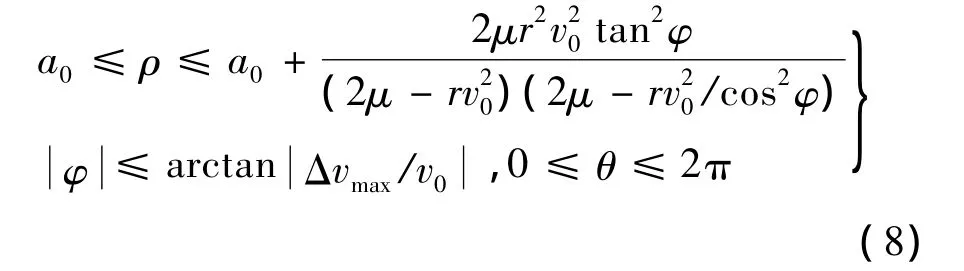
2.3 單脈沖作用下圓軌道在軌攔截器覆蓋范圍
任意方向、大小單脈沖作用時,可看成兩個過程的疊加,平面脈沖改變軌道半長軸,垂直軌道面脈沖改變軌道傾角和軌道半長軸。綜合2.1節和2.2節模型可得在軌攔截器覆蓋范圍為一曲面繞z軸旋轉形成的包絡區域,數學描述為:
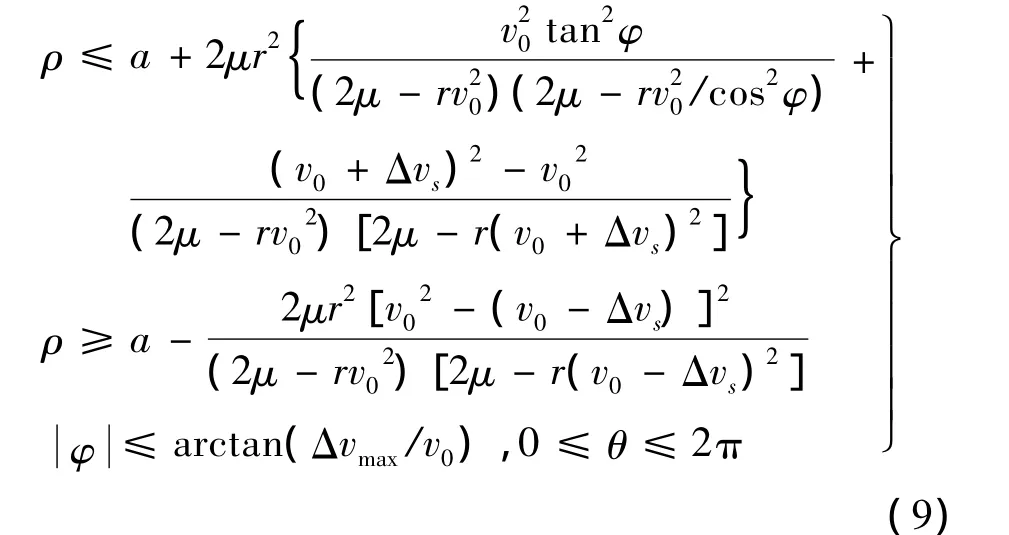
3 橢圓軌道在軌攔截器覆蓋能力
3.1 平面脈沖作用下在軌攔截器覆蓋范圍
平面脈沖ΔvR作用下,在軌攔截器生成軌道的動量矩 h1和偏心率e,計算如下[10-11]:
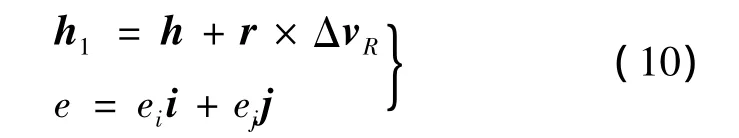
式中,i,j為近焦點坐標系 x,y軸的單位矢量;ei,ej為偏心率e在x,y軸的分量值,計算如下:
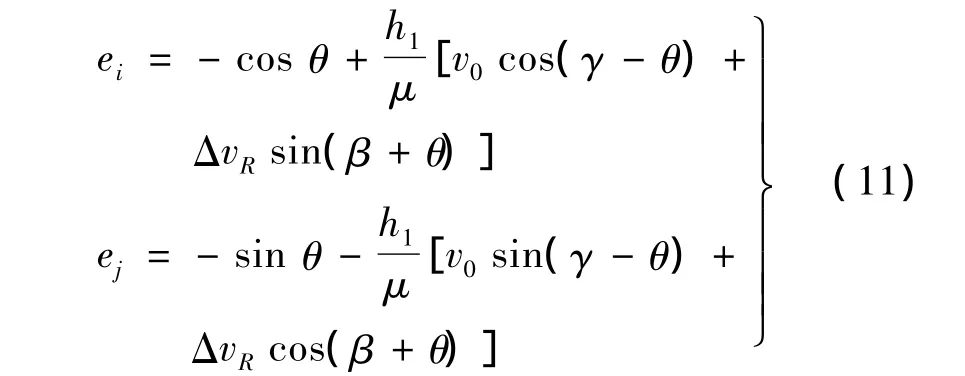
式中,θ為脈沖施加點的真近點角;γ為脈沖施加點在軌攔截器速度矢量與矢徑垂線方向夾角。
θ,β 在[0,2π)變化時生成軌道曲線族[5],生成的軌道半徑統一描述為:
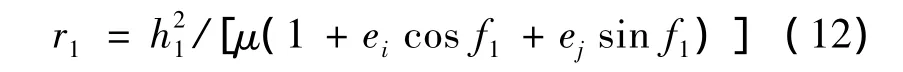
式中,f1為生成軌道上某點矢量與x軸夾角。
根據包絡線的定義,曲線族的包絡線即為在軌攔截器覆蓋范圍的邊界。在軌攔截器覆蓋范圍的內外邊界計算[5]如下:
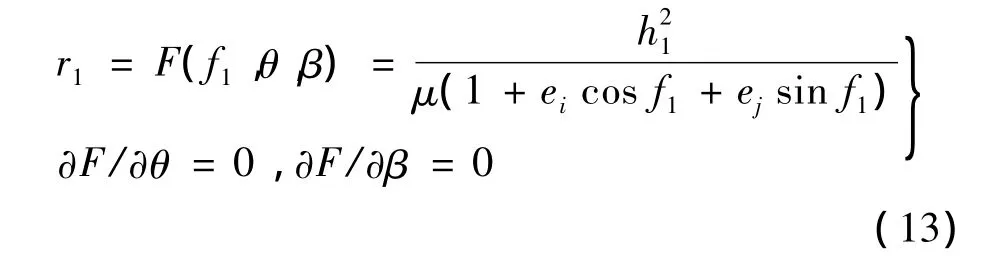
對上式進行求解,得到平面脈沖作用下在軌攔截器覆蓋范圍,具體求解過程參見文獻[5]。
3.2 垂直軌道面脈沖作用下在軌攔截器覆蓋范圍
初始軌道為橢圓軌道,在垂直軌道面的脈沖作用下,用位置矢量描述在軌攔截器的覆蓋范圍較為復雜,本節用軌道根數描述垂直軌道面脈沖作用下在軌攔截器的覆蓋范圍。
在垂直軌道面脈沖作用下,根據高斯攝動方程得到在軌攔截器的軌道根數變化如下:
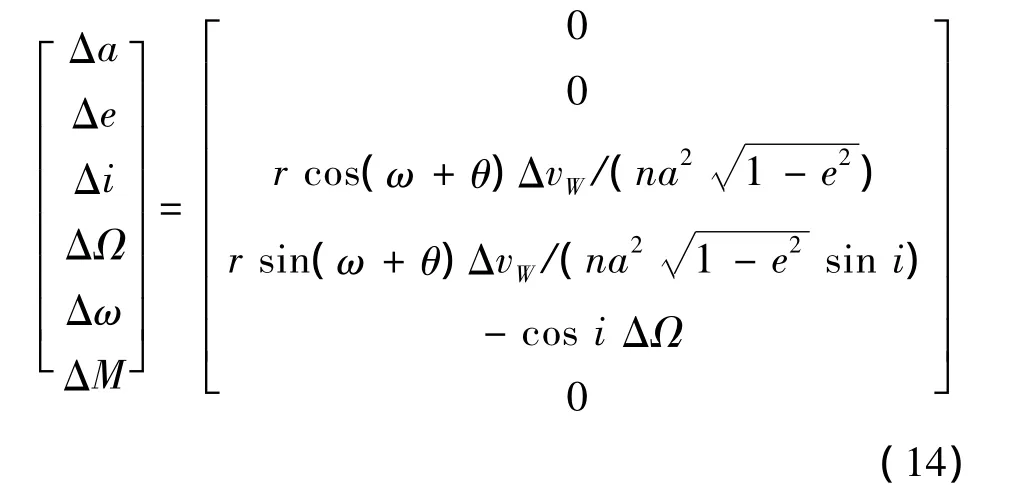
式中,Δa,Δe,Δi,ΔΩ,Δω,ΔM 為軌道根數變化量;n為平均運動常數。暫不考慮高斯攝動方程極值點情況,從式(14)可以得出,Δi,ΔΩ,Δω中兩個變量獨立。選Δi,ΔΩ作為描述在軌攔截器覆蓋范圍的參數,它們滿足:
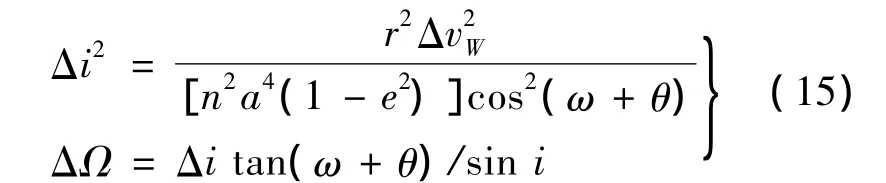
3.3 單脈沖作用下橢圓軌道在軌攔截器覆蓋范圍
在軌攔截器初始軌道為橢圓軌道,當有任意方向、大小的單脈沖作用時,可把該沖量看成平面脈沖和垂直軌道面脈沖的疊加。綜合3.1節和3.2節模型,將(Δi,ΔΩ,r)作為描述在軌攔截器覆蓋范圍的參數。Δi和ΔΩ確定時,施加脈沖真近點角θ的位置確定,則式(13)退化為:
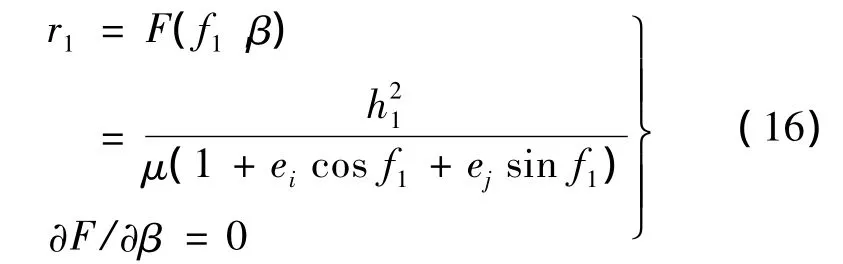
對上式求解,得到真近點角θ與β的關系[5],聯立式(15)得到單脈沖作用下在軌攔截器覆蓋范圍的數學描述如下:
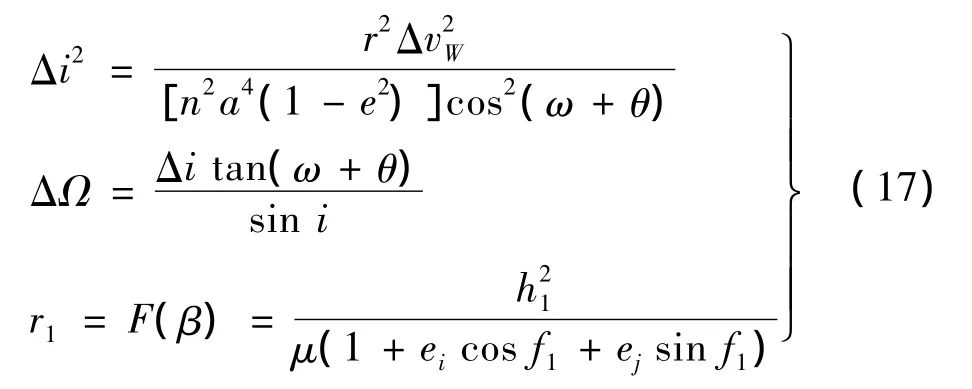
4 仿真計算及結果分析
4.1 初始軌道為圓軌道的情況
仿真條件取為:r=8 000 km,v=7.059 km/s,Δvmax=0.3 km/s。圖2給出了平面脈沖作用下在軌攔截器的覆蓋范圍。
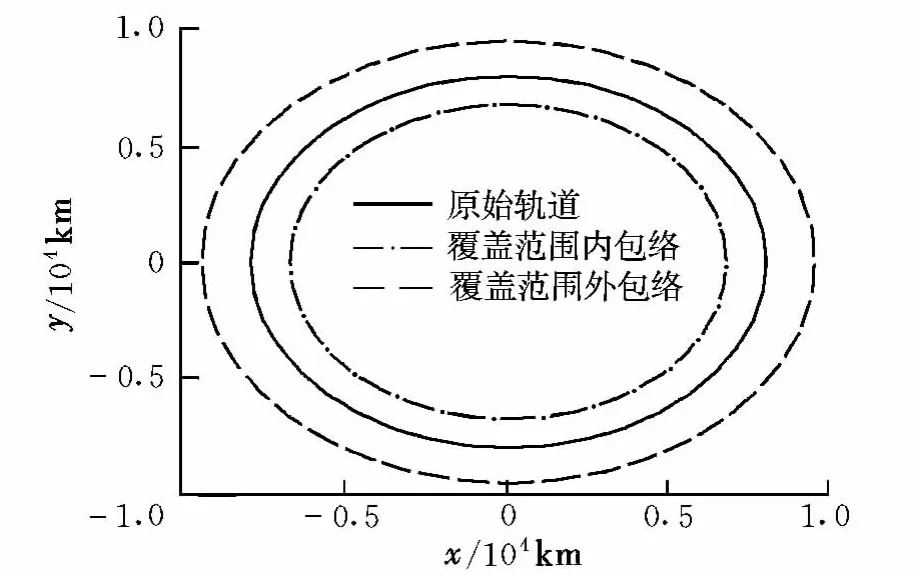
圖2 在軌攔截器覆蓋范圍(平面脈沖)Fig.2 Coverage area of orbit-interception(coplanar impulse)
垂直軌道面脈沖作用下為繞近焦點坐標系z軸的旋轉體,沿z軸且x>0切面如圖3所示。
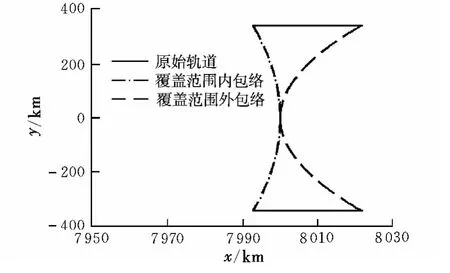
圖3 覆蓋范圍切面圖(垂直軌道面脈沖)Fig.3 Section diagram of coverage area(vertical impulse)
任意方向、大小單脈沖作用下,在軌攔截器的覆蓋范圍也是繞近焦點坐標系z軸的旋轉體,沿z軸且x>0切面如圖4所示。
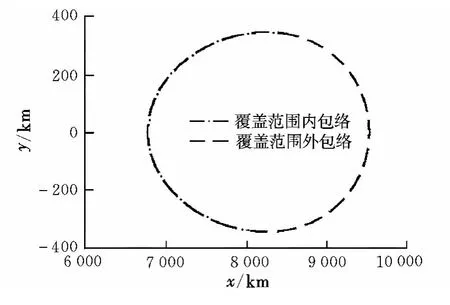
圖4 覆蓋范圍切面圖(任意方向)Fig.4 Section diagram of coverage area(any direction)
4.2 初始軌道為橢圓軌道的情況
仿真條件設置為:(a,e,i,Ω,ω,M)=(20 000 km,0.5,30°,45°,60°,0°),Δvmax=0.3 km/s。圖 5給出了平面脈沖作用下在軌攔截器覆蓋范圍。垂直脈沖作用下Δi,ΔΩ的變化范圍如圖6所示。任意方向、大小作用下,ΔΩ=0時在軌攔截器覆蓋范圍如圖7所示。圖8給出了ΔΩ=0時在軌攔截器覆蓋范圍。
從仿真結果可以看出,當最大變軌能力給定時,利用文中方法可以快速確定單脈沖作用下在軌攔截器的覆蓋范圍。
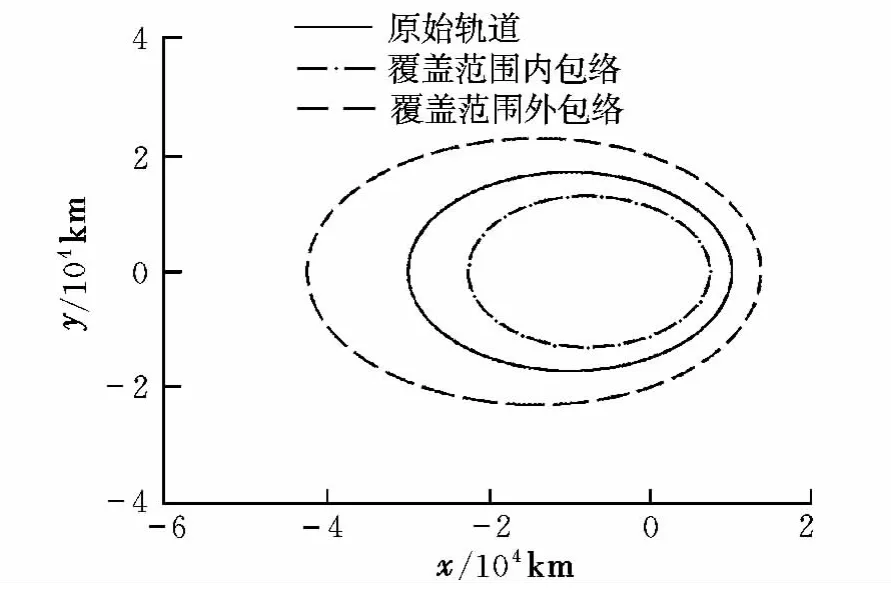
圖5 在軌攔截器覆蓋范圍(平面脈沖)Fig.5 Coverage area of orbit-interception(coplanar impulse)
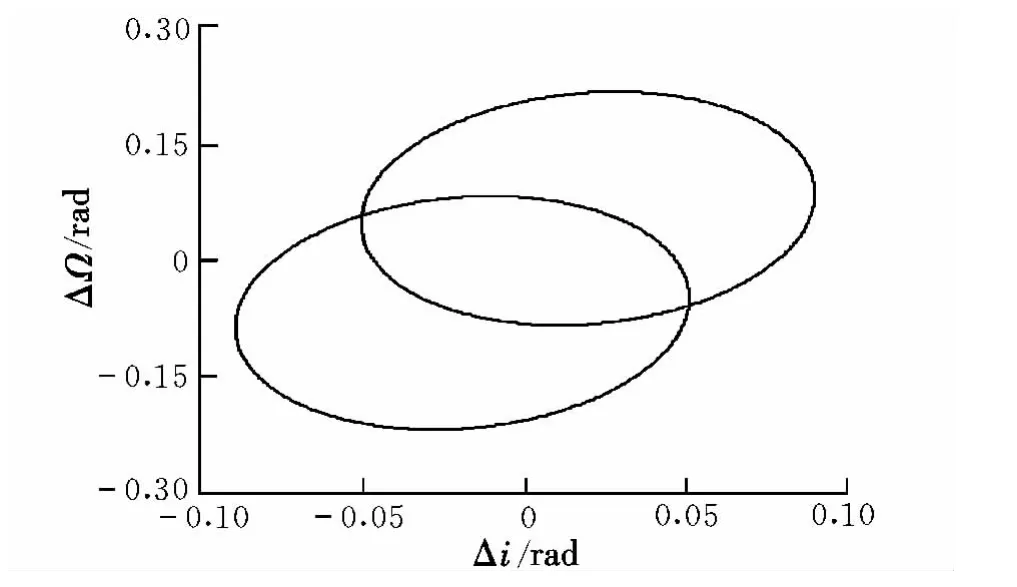
圖6 在軌攔截器覆蓋范圍(垂直軌道面脈沖)Fig.6 Coverage area of orbit-interception(vertical impulse)
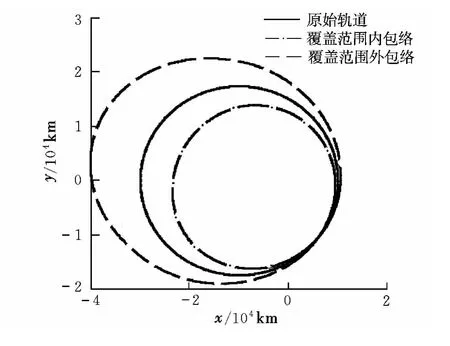
圖7 在軌攔截器覆蓋范圍(Δi=0,ΔΩ=0)Fig.7 Coverage area of orbit-interception(Δi=0,ΔΩ =0)
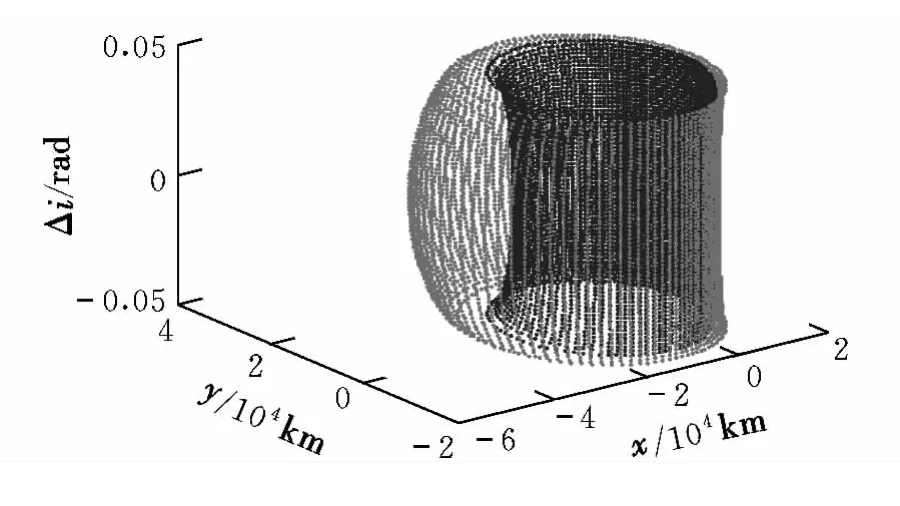
圖8 在軌攔截器覆蓋范圍(ΔΩ=0)Fig.8 Coverage area of orbit-interception(ΔΩ =0)
5 結束語
作為動能型在軌攔截器實施機動及優化的前提,在給定最大變軌能力下的覆蓋范圍研究具有重要意義[12]。本文利用運動方程及高斯方程,分別研究了初始軌道為圓軌道及橢圓軌道在共面、垂直軌道面脈沖、任意方向脈沖作用等三種情況下在軌攔截器的覆蓋范圍。仿真表明,文中模型能夠簡捷有效地確定在軌攔截器的覆蓋范圍,為機動軌道設計與優化前提判斷以及在軌攔截器的軌道設計提供技術支持。
[1] Kamel O M,Soliman A S.On the optimization of the generalized coplanar Hohmann impulsive transfer adopting energy change concept[J].Acta Astronautica,2005,56(4):431-438.
[2] 李雪華,和興鎖,仲勤芳.單脈沖作用下衛星軌道的可達區域研究[J].西北工業大學學報,2011,29(1):114-117.
[3] 雪丹,李俊峰,寶音賀西.平面脈沖作用下衛星軌道的可達范圍研究[J].宇航學報,2009,30(1):88-92.
[4] 雪丹,李俊峰.確定衛星可達范圍的優化方法[J].清華大學學報(自然科學版),2009,49(11):1825-1855.
[5] 雪丹,李俊峰,蔣方華.衛星在軌道平面內的可達范圍研究[J].力學學報,2010,42(2):337-342.
[6] 常燕,周軍.空間飛行器追蹤區設計[J].宇航學報,2006,27(6):1228-1232.
[7] 陳茂良,周軍,常燕.空間攔截攻擊區和威脅區仿真研究[J].航天控制,2009,27(1):41-48.
[8] 周建華,徐波,馮全勝.軌道力學[M].北京:科學出版社,2009:59-61.
[9] 楊嘉墀,范劍峰,范秦鴻.航天器軌道動力學與控制[M].北京:宇航出版社,1995:54-56.
[10] Vinh N X,Gilbert E G,Howe R M,et al.Reachable domain for interception at hyperbolic speeds[J].Acta Astronautica,1995,35(1):1-8.
[11] Ranieri C L.Path-constrained trajectory optimization for proximity operations[R].AIAA-2008-6275,2008.
[12]曹裕華,馮書興,管清波.航天器軍事應用建模與仿真[M].北京:國防工業出版社,2010:1-8.

