地磁姿態探測器的實時標定方法研究

楊宇彬，湯國建，包為民

(1.國防科學技術大學航天科學與工程學院，湖南長沙410073;2.四川航天系統工程研究所，四川成都610100;3.中國航天科技集團公司科技委，北京100830)

0 引言

地磁場是地球固有物理矢量場，具有穩定、隱蔽、難以人為干擾的特性。自從1989年美國Cornell大學Psiaki等人率先提出利用地磁場確定衛星軌道概念以來，這一方向逐漸發展成為國際導航領域的研究熱點，所衍生出的地磁導航、地磁制導與地磁姿態探測是航空、航天領域重要的研究方向。

地磁測量具有無輻射、全天時、全天候、全地域的特征，與其他有源制導、導航或探測方式相比，地磁測量在軍事領域有著無可比擬的優勢。使用地磁制導的導彈抗干擾性能強、突防能力強，俄羅斯新型機動變軌的SS-19導彈采用地磁等高線制導系統，實現了導彈的變軌制導［1］，以對抗美國的反彈道導彈攔截系統。SS-19導彈再入大氣層后，不按拋物線飛行，而是沿地磁等高線飛行，使美國導彈防御系統無法準確預測導彈的飛行軌跡，增強了導彈的突防能力。法國正在研究一種全新的以地磁測量為基礎的炮彈制導系統。德國則研究了基于卡爾曼濾波的地磁導航系統，應用于導彈并成功試射。近年來，國內工業界和學術界也十分重視地磁姿態測量、地磁導航的應用研究。由于地磁測量的成本低、無輻射、隱蔽性好、全天候、抗沖擊振動特性好，特別適合用于導彈實時姿態探測。但是，工程實用尚需解決地磁測量易受鐵磁性物質或其他設備引起的磁場畸變影響、溫度漂移、強磁干擾等問題，磁差標定與補償是工程應用的研究重點。

本文針對當前普遍采用的磁差標定方法不適用于導彈飛行環境的工程問題，提出了一種實時磁差標定與補償方法。

1 地磁場模型

地磁場具有磁位特征，即:

式中，B為地磁場強度矢量;U為地磁場磁位。通常采用當地地理坐標系OxTyTzT來描述磁場強度分量，可以得到沿坐標軸xT，yT，zT三個方向磁場強度的分量為:

式中，r為空間一點距地心的距離;RE為地球平均半徑;λ為格林尼治起算的東經;θ為余緯;為n次m階Lefendre函數為基本磁場的高斯系數。實測表明，采用國際參照地磁場(IGRF)模型即具有滿意的精度。

2 磁傳感器靜態磁差標定方法

2.1 工作原理

磁阻傳感器是利用合金電阻對某一個方向磁場敏感的原理制成。由于磁傳感器體積小且沒有活動部件，功耗很低，配合選用體積小、功耗低的外圍器件，可以將探測器微型化，已經有逐步取代磁通門的趨勢，因此，非常適合導彈、火箭等飛行器使用。

2.2 靜態磁差標定

磁傳感器因制造和環境影響，測量時會產生誤差，一般分安裝誤差、零偏、刻度因子誤差和非正交誤差。因此，實際應用需對磁傳感器的誤差進行補償。

基于補償精度和工程可實現性要求，建立如下磁傳感器輸出模型:

式中，Uhx，Uhy，Uhz為磁傳感器的輸出;Uhx0，Uhy0，Uhz0為磁傳感器零位;Kx，Ky，Kz為磁傳感器標度因數;Hx，Hy，Hz為磁傳感器輸入的激勵磁場強度;Kxy，Kxz，Kyx，Kyz，Kzx，Kzy為磁傳感器的安裝誤差系數。

靜態磁差標定可基于位置試驗對模型中的參數進行辨識，采用12位置標定方法來確定磁傳感器模型中的系數［2］。靜態磁差標定通常在產品交付前由研制廠家完成，標定系數燒寫在彈載計算機內置的Flash芯片內。

3 磁傳感器實時動態標定算法

3.1 橢圓擬合標定算法

現有的標定方法分三步依據磁傳感器的輸出辨識標定系數［3］，補償溫度引起的零偏、靈敏度漂移、導彈自身鐵磁干擾以及其他異常磁干擾引起磁場畸變導致的影響。算法步驟如下［4］:

(1)確定旋轉因子

圖1為橢圓旋轉示意圖。首先將橢圓旋轉δ角度，此時橢圓長軸由原來的r轉到r'的位置。取長短軸平方和的最大值，令

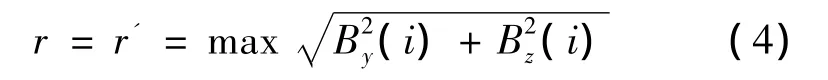
可得此時轉角δ有如下關系式:

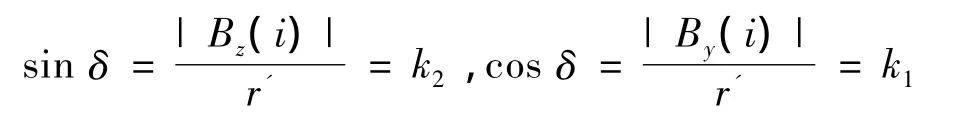
(2)確定伸縮因子，將橢圓修正成圓

在使用環境中，磁傳感器輸出數據經第一步旋轉后，記錄Y，Z軸的最大值和最小值，通過伸縮變換，將橢圓修正成圓，伸縮因子為:

(3)平移因子，將圓心與坐標原點重合

經旋轉和伸縮后的地磁數據圓心并不與坐標原點重合，需進行平移，平移因子為:

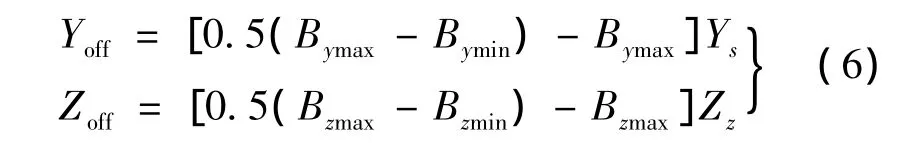
該算法在試驗室條件下被證實是有效的，但首次應用于某項目飛行試驗中未獲得滿意的結果。事后分析表明，由于該項目導彈執行機構采用了電磁閥驅動舵機動作，電磁閥工作瞬間產生的強磁脈沖信號疊加了磁干擾，該異常磁信號未被硬件濾波器以及FIR軟件濾波器濾除，而直接用于實時動態標定，導致標定失效，滾轉姿態測量失效。為解決該工程實際問題，必須研究專用的異常磁信號濾除算法。

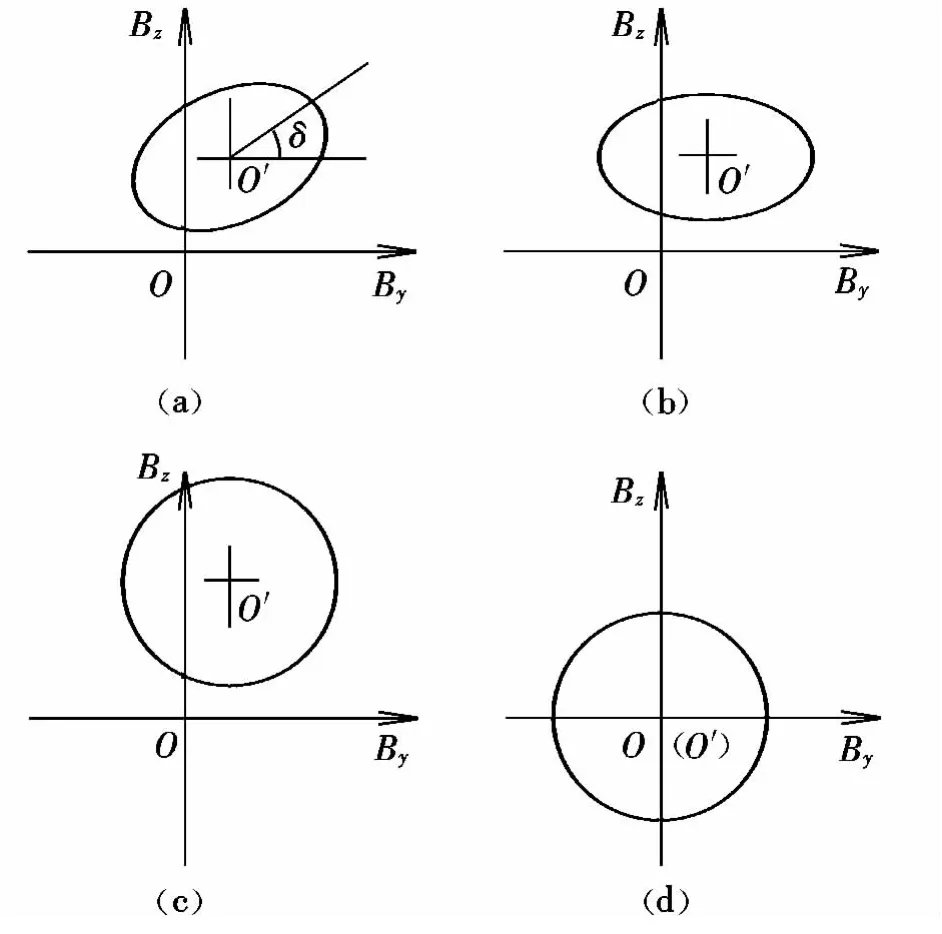
圖1 橢圓旋轉補償法Fig.1 Method of the ellipse rotation compensation

3.2 異常磁信號濾除算法

本文提出的異常磁信號濾除算法的思路是:首先使用白噪聲多項式最優線性移動平滑算法對磁采樣數據進行預處理，通過預測下一采樣時刻傳感器的輸出濾除可能出現的野值，濾除異常信號的采樣序列可用于3.1節描述的標定算法。

按移動平滑的基本思想，在連續采樣的數個毫秒內，傳感器的輸出x(i)總能用一個時間變量的p階多項式描述，假設磁傳感器的輸出為:

式中，P(i)為p階多項式;ε(i)為白噪聲序列。

用一組時間函數的多項式族{pj(i)，j=0，1，…，p}的線性組合來表示P(i)，可簡化多項式計算過程，即 ，其中 θj為系數。將式(7)寫為矩陣形式X=Pθ+ε，其中:

式中，N為窗口寬度，則:

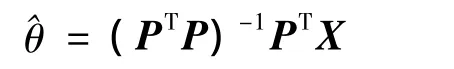
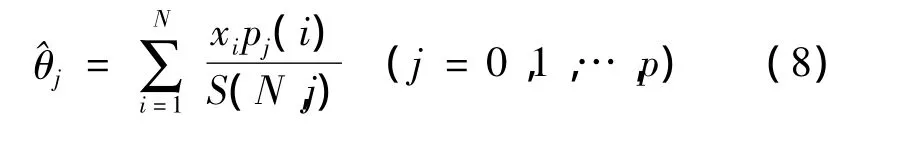
由式(7)得到擬合曲線:

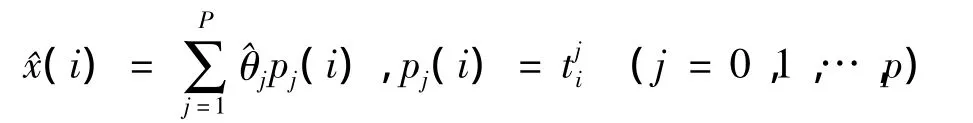
計算^x(i)在N+a處的零階微商的最優線性無偏估計，得:

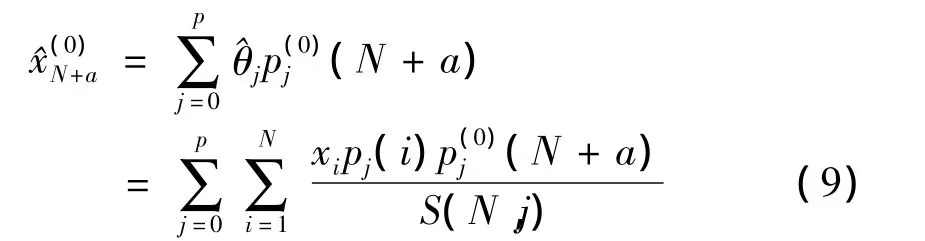
即權系數的無偏最優估計為:

式中，a為濾波位置點。當a=l時定義為l步預測算法;a=0時為濾波算法;a=－(N－1)/2時為中心平滑算法。本文取a=l=1進行一步預測。顯然，一旦確定了“窗口”寬度N和模型階數p，則預測算法的權系數也隨之確定。記序列{x(n－N+1)，…，x(n)}對x(n+1)的預測為 ^xn|n+1，有:

具體操作中，首先可從飛行試驗遙測數據中取出連續的N個磁數據進行p階多項式擬合，通過試算和全局要求確定參數N和p的具體值，由式(10)計算出 N 個權系數 WN－i(i=1，2，…，N);然后將這些權系數作為一個“窗口”存儲在彈載計算機中，對于觀測數據序列只需由式(11)計算一步預測值。該算法為一種動態預測方法，當后繼測量xn+1滿足時，判定xn+1為野值，用預測值代替，其中μ為判別閾，需根據實際情況選擇，閾值取得過小會引起誤判。實際使用時取為離線辨識的幅值參數，m的取值由采樣頻率和導彈的彈道特性確定。

3.3 標定補償算法對比驗證情況

通過地面轉臺和飛行試驗驗證異常磁信號濾除算法以及標定算法的效果。

3.3.1 轉臺驗證

轉臺試驗中，導彈執行機構的電磁鐵按設計頻率工作。未采用異常磁數據濾除算法時，計算的滾轉角與轉臺碼盤角度對比如圖2所示，可見顯著跳動。采用異常磁數據濾除算法后，標定并補償的磁數據如圖3所示，計算的滾轉角與碼盤角度對比如圖4所示。可以看出，計算的滾轉角與轉臺碼盤角度一致性好，可見野值濾除算法的效果明顯。采用本文提出的異常磁數據濾除算法后，標定、補償的精度顯著提高，不同轉速情況下的滾轉角測量誤差總小于1°，滿足工程應用需要，詳見表1。

圖2 滾轉角對比圖Fig.2 Comparison of roll angle

圖3 補償后的地磁信號Fig.3 Geomagnetic signals after compensation

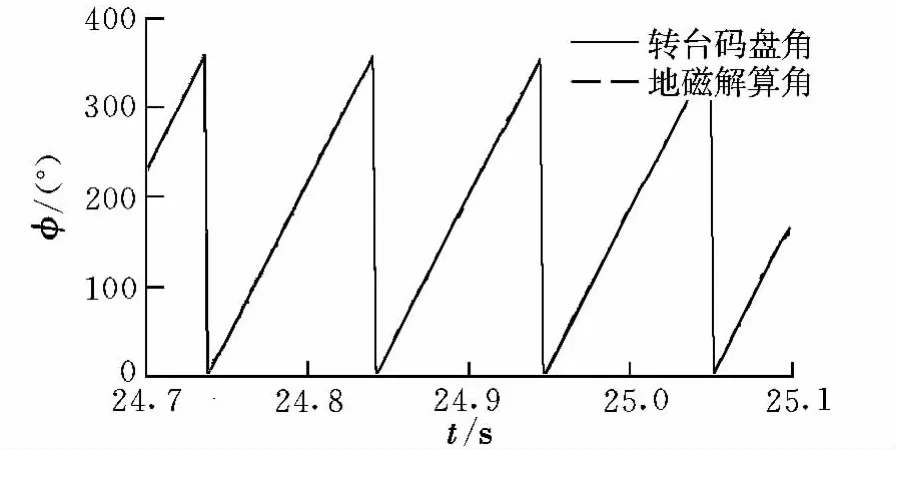
圖4 補償后的滾轉角對比圖Fig.4 Comparison of roll angle after compensation

表1 不同轉速下滾轉角測量誤差 (°)Table 1 Roll angle error of different revolutions

3.3.2 飛行試驗驗證

導彈飛行試驗采用本文提出的磁數據預處理與標定算法，結果表明算法能可靠濾除執行機構動作引起的磁信號野值，詳見圖5;彈上計算機實時解算的滾轉角見圖6，經實時標定補償后，磁解算滾轉角線性度有所提高。

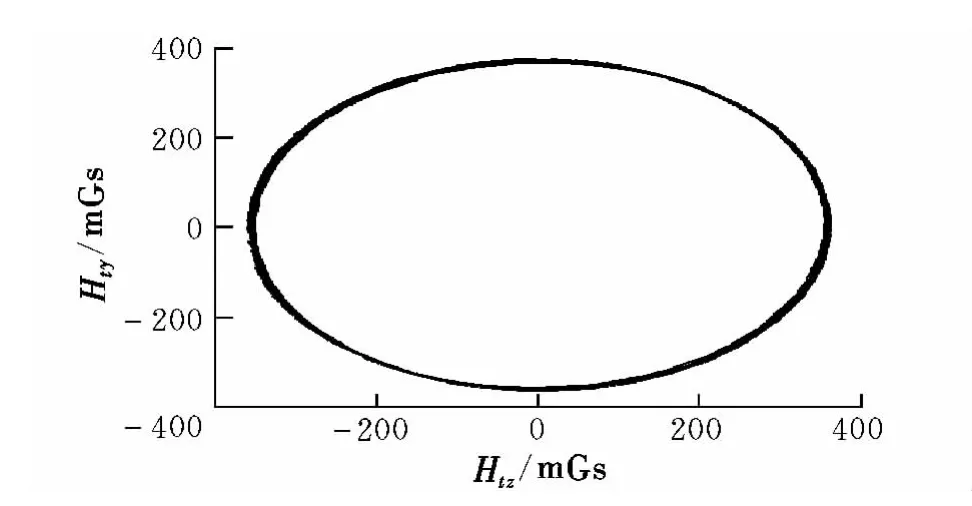
圖5 飛行中標定后的磁信號Fig.5 Magnetic signals after in-flight calibration

圖6 飛行中標定補償后的滾轉角Fig.6 Roll angle after in-flight calibration compensation

實測表明，進行一次實時標定耗時約0.7 ms，而計算周期為1 ms，即在一個計算周期內能實現快速標定，并將標定結果用于補償下一計算周期磁采樣數據;磁采樣到來時，標定與補償遞推進行，實時性滿足某轉速高達10 r/s的導彈制導控制的要求。

4 結束語

本文提出的實時磁差標定與補償方法重點解決了異常磁信號野值濾除問題。該方法經轉臺試驗與飛行試驗驗證，具有魯棒性優、精度高、實時性好的特點，解決了傳統磁差標定方法獲取的補償系數不適用于某型號高速滾轉導彈姿態探測的問題，具有工程應用價值。

［1］ 李素敏.地磁場資源在匹配制導中的應用研究［J］.制導與引信，2004，(3):19-21.

［2］ 張嬌，陳靜，楊栓虎.三軸磁阻式傳感器標定方法研究［J］.彈箭與制導學報，2010，30(6):46-48.

［3］ 邵婷婷，馬建倉，胡士峰，等.電子羅盤的傾斜及羅差補償算法研究［J］.傳感技術學報，2007，20(6):1335-1337.

［4］ 史連艷，宋文淵，王紅云.基于旋轉因子的磁傳感器誤差補償改進橢圓法［J］.探測與控制學報，2010，32(2):5-8.