基于改進差分進化算法的PIO預測評估方法

李琳，陳云翔，李千，紀小檸

(1.空軍工程大學 機要系，北京100195;

2.空軍工程大學裝備管理與安全工程學院，陜西西安710051;3.空軍裝備部，北京100843;4.空軍指揮學院，北京100097)

0 引言

隨著高增益電傳操控系統在現代飛機上的廣泛應用，PIO發生的概率不斷增加［1］，至今已造成多起機毀人亡的事故。因此，如何通過系統、高效的方法對PIO進行預測評估，是飛機研發階段和飛行安全保障工作中面臨的重要課題。目前國外已研發出多種PIO預測準則，為新型飛行器的研發和飛行控制系統設計、解決PIO問題、保障飛行安全提供了重要的理論依據。從國內研究現狀來看，PIO領域的研究仍處于理解和運用國外已有準則和方法階段，并且對PIO預測評估方法的研究不系統，缺少驗證PIO預測準則的飛行模擬與飛行試驗，未建立類似于國外的PIO評估數據庫，與國外仍然存在不小的差距。我國在該領域仍需進一步展開研究，以使我國的飛行器安全性設計水平與國際接軌。

本文提出了一種基于改進差分進化算法的PIO預測評估方法，以速率限制II型非線性PIO為例，構建了基于速率限制因素的人機閉環系統模型，根據Gap準則運用該算法對人機系統PIO進行預測評估。

1 改進型差分進化算法

目前全局搜索優化算法主要包括遺傳算法(GA)、粒子群進化算法(PSO)和差分進化算法(DE)。與其他兩類優化算法相比，DE算法結構簡單，便于操作，經驗型參數設置最少，且DE算法的收斂和優化效率相對優于GA和PSO算法。但基本型DE算法的參數被預先設定，并且在優化過程中一成不變，很難實現算法搜索與開發能力的平衡。針對DE算法的局限性，提出了一種基于混沌理論與高斯擾動的改進型差分進化(Differential Evolution Based on Chaos Theory and Gaussian Disturbance，CTGDDE)算法，圖1給出了該算法的流程圖，具體步驟與算法性能驗證見文獻［2］，其基本思想是通過引入混沌理論進行局部搜索以提高算法的尋優能力;通過在交叉階段引入高斯擾動算子來防止算法陷入局部最優，從而兼顧實現算法的局部尋優和全局尋優。

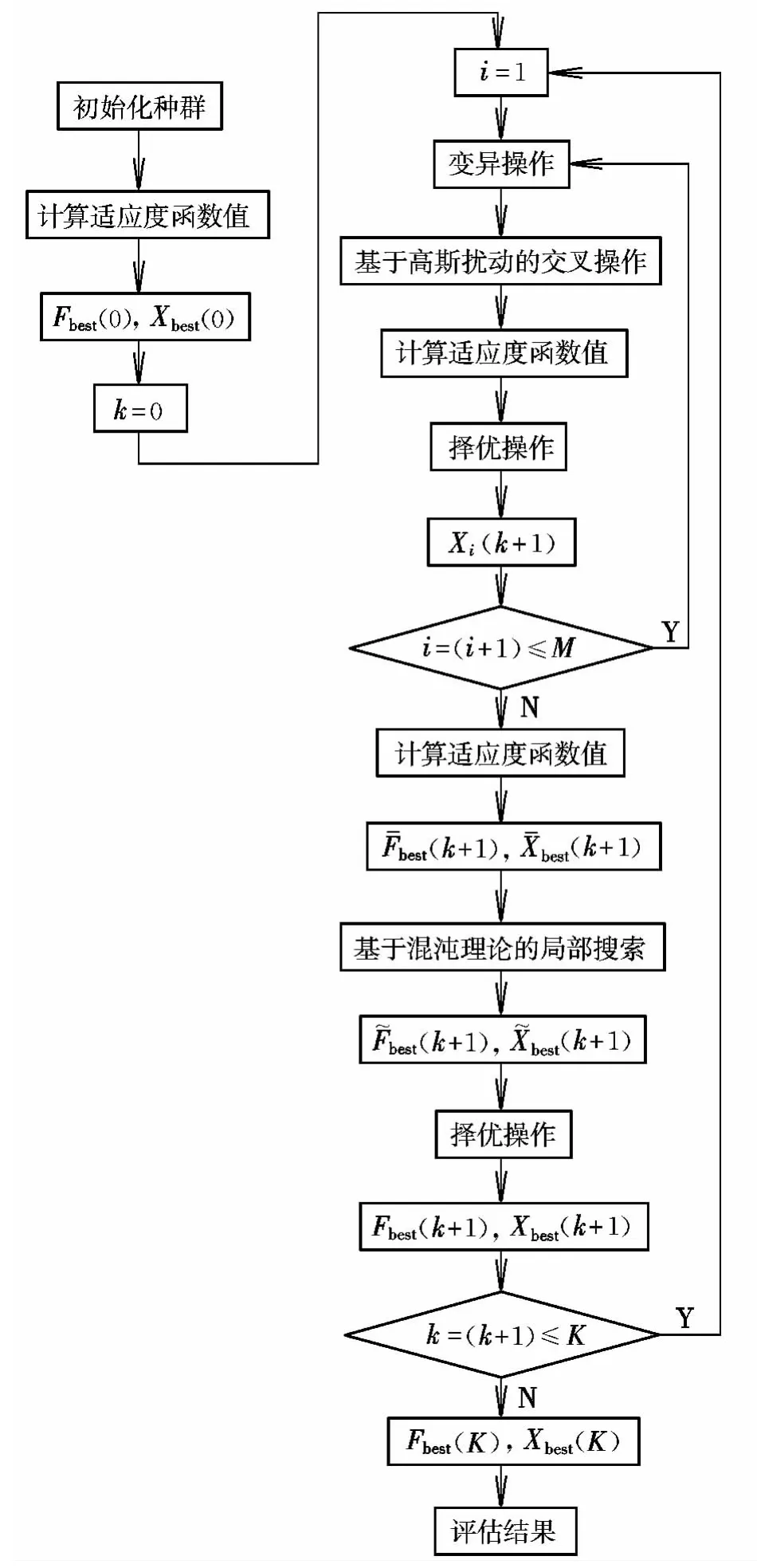
圖1 CTGDDE算法流程圖Fig.1 Process of CTGDDE algorithm

2 PIO預測評估方法

人機系統PIO預測評估的最終目的是確認所設計的控制系統能夠保證飛機在所有飛行包線和飛行參數變化范圍內都能匹配飛行員特性并安全穩定地完成任務，同時具有良好的飛行品質。具體而言，基于CTGDDE算法的人機系統PIO預測評估問題可描述為針對人機系統PIO評估的相關準則，根據具體的飛行任務建立人機系統閉環模型，設計并求解適應度函數的優化問題，進而搜索最壞情況及其人機系統狀態參數的集合，從而給出評估結論及設計更改建議，其具體步驟如下:

(1)初始化。確定待評估的飛行狀態，根據飛行任務與設計要求設置人機系統不確定狀態參數及其變化范圍;

(2)根據飛行任務和飛行狀態建立相應的飛行員控制行為模型、飛機本體動力學模型及其傳遞函數和控制系統模型，并構建該模式下的人機閉環回路;

(3)確定人機系統PIO預測評估準則，根據人機閉環模型建立相應的適應度函數，即將人機系統PIO評估轉化為適應度函數的優化問題;

(4)將標稱狀態的參數值代入適應度函數，檢驗飛行控制系統的設計是否與飛行員特性相匹配，即該設計是否滿足人機PIO準則的要求。若均滿足，則執行步驟(5)，否則該設計未達標，轉入步驟(7);

(5)通過文獻［2］提出的CTGDDE算法對適應度函數展開優化運算，即在不確定參數變化空間內搜索飛行狀態最壞情況下的參數集合;

(6)根據最壞情況下的適應度函數值判斷該情況下的控制系統設計是否滿足人機系統穩定性要求，若滿足，則保存分析結果，否則該控制系統設計未達標;

(7)轉入下一飛行狀態進行評估;

(8)遍歷飛行包線范圍內所有飛行狀態，若所有狀態均滿足人機PIO準則要求，則該飛行控制系統設計通過該準則確認，否則未予確認，需進行改進后再予以評估。

需要注意的是，為了更全面準確地對控制系統進行評估，通常采用多個人機系統PIO預測準則對其進行驗證;在人機閉環系統建模方面，也應考慮實際任務的多樣性，結合多種飛行員控制行為模式對飛行控制系統展開評估。

3 模型的建立

由于PIO屬于人機閉環不穩定振蕩，故閉環操縱是其必要條件。因此，構建人機閉環控制系統模型是研究PIO問題的基礎。本文對基于速率限制環節的Ⅱ型PIO進行預測評估，首先要建立基于速率限制因素的人機閉環系統模型，其俯仰軸模型如圖2所示。

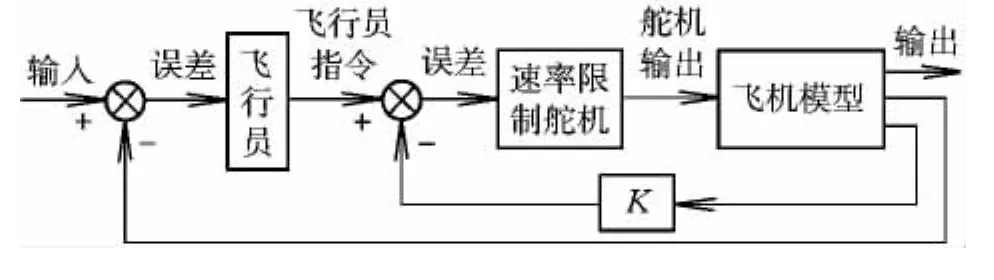
圖2 基于速率限制因素的人機閉環系統模型Fig.2 Human machine system model based on rate-limit

圖2 中，速率限制舵機模型可進一步分解，如圖3 所示［3］。

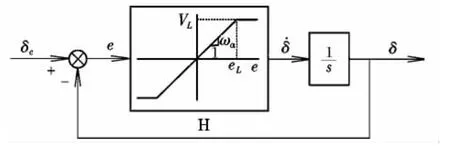
圖3 舵機速率限制模型Fig.3 Rate-limit model

操縱面偏角指令δc經速率限制模型后輸出操縱面偏角信號δ，通過偏角的實時反饋信息，使之形成閉環回路，其中前向通道誤差信號e=δc－δ作為非線性飽和環節H的輸入，飽和模塊的輸出是操縱面速率δ˙，通過對該信號進行積分運算可得到操縱面偏角信號δ。非線性飽和模型H可通過以下3個參數進行描述:飽和值VL，即舵機速率的限制值;增益值ωα，即模型H中線性部分的斜率，其值等于線性舵機閉環帶寬或簡化等于線性帶寬;速率飽和閾值eL=VL/ωα，當前向通道輸入的誤差值e＜eL時，環節H可簡化為線性一階滯后模型，其響應取決于時間常數T=1/ωα。相應地，當輸入誤差值e＞eL時，操縱面速率限制環節將被激活，該模式下會呈現出完全的非線性，其特點是。有研究表明，該模式下的響應特性完全獨立于線性部分的時間常數T，而取決于其輸入幅值與速率限制，非線性與線性時間常數比滿足如下關系式:

在實際研究中，通常采用描述函數的方法來研究速率限制模型等非線性系統，當輸入信號δc=A sin(ωt)時，舵機速率限制模型中的飽和非線性環節可描述為:

式(2)也稱為速率限制作用下舵機高度飽和時的正弦輸入描述函數模型，其形成的機理是由于輸入誤差值在大多數時間大于速率飽和閾值eL，造成系統長時間處于非線性狀態。相應地，當輸入誤差在少數時間超過eL時，系統輸出僅間斷性地出現速率限制，其響應呈現擬線性特征，該模式稱之為近飽和狀態，此模式下的正弦輸入模型可描述為［4］:

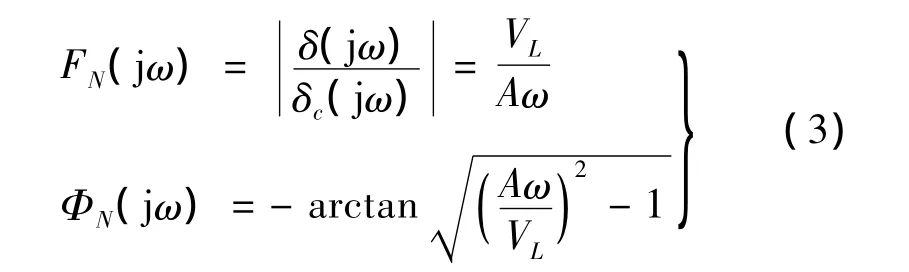
當速率限制高度飽和且舵機帶寬趨于無窮時，高度飽和正弦輸入模型可描述為正弦輸入/三角輸出的近似描述函數模型，具體表述為［5］:

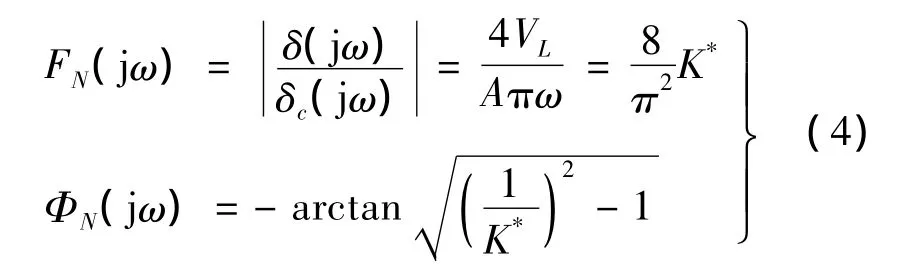
這里引入參數 K*= πVL/(2Aω)= πTωα/(2TNω)，且 K*∈［0，1］，其數值反映了系統速率限制的嚴重程度，當K*→0時，速率限制作用增強，系統呈現非線性，表現為幅值衰減，相位滯后增加;相應地，當K*→1時，速率限制作用減弱，系統的線性部分增強。

對比式(2)、式(3)和式(4)，不難發現，前兩式僅差一個比例常數π/4;而第3式的幅頻函數與第1式相同。實踐表明，在三者的應用方面，需滿足以下條件:

(1)當0.2≤T/TN＜0.8時，采用高度飽和正弦輸入描述函數模型;

(2)當T/TN≥0.8時，采用近飽和正弦輸入描述函數模型;

(3)當T/TN＜0.2時，采用正弦輸入/三角輸出描述函數模型。

4 實例分析

本文選用Gap準則對Ⅱ型PIO進行預測評估，Gap準則及其使用規范在文獻［6］中有詳細敘述，在此不加贅述。假設某飛機舵機帶寬為ωα=35 rad/s，速率限制值為VL=30(°)/s，最大可用偏角值Amax=30°。在飛機線性運動模型方面，選取該型飛機在高度為1.5 km，馬赫數為0.2處為標稱狀態，設定飛機質量、y軸轉動慣量、氣動參數和為攝動參數，該機型在標稱狀態下的俯仰傳遞函數為:

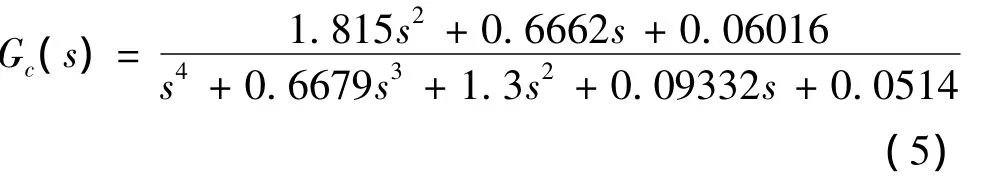
根據傳遞函數可求出飛機的中性穩定頻率ω0=9.5 rad/s。由于ωα?ω0，飛機舵機可認定為滿足無限帶寬條件，因此，可選擇正弦輸入/三角輸出描述函數為飛機舵機的數學描述模型。

大量事實表明，Neal-Smith飛行員模型在一定程度上可以較全面地反映飛行員的控制特性，根據美軍標中關于Neal-Smith飛行員駕駛模型的確定準則，建立飛行員駕駛模型為:

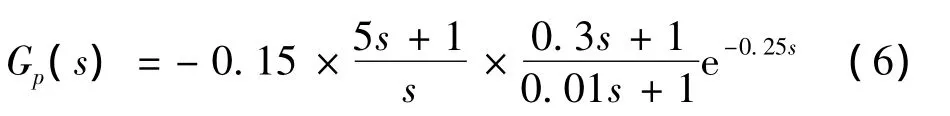
首先通過Matlab 2010a可獲得Gc(s)Gp(s)與速率限制舵機負倒數描述模型F(A，jω)的Nichols曲線，如圖4所示。

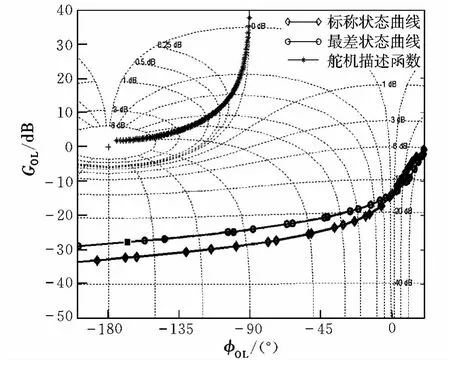
圖4 標稱情況與最差情況下的Nichols曲線Fig.4 Nichols curves of the normal case and the worst case

根據Gap準則可知，該情況屬于Ⅰ類應用模式，求解使兩條曲線恰好相切時飛行員需增加的有效增益的最小值ΔKp=34.3842 dB，相對應的K*=0.9675，ω=16.4 rad/s。因此，根據 Gap準則可計算出導致PIO的飛機舵機偏角幅值為:

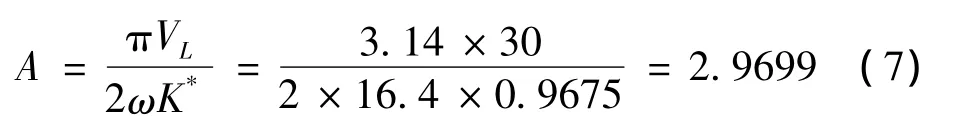
通過Gap準則，可計算出標稱狀態下的準則參數G為:

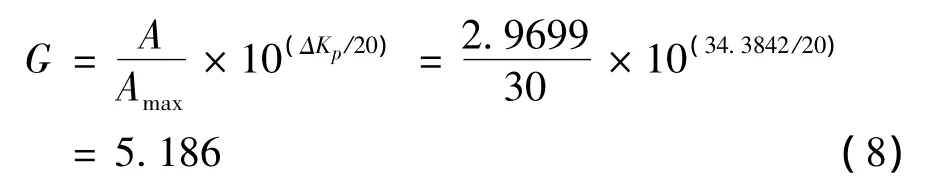
由于G＞1，因此，飛機在設計點處符合準則要求。根據Gap準則，構建Ⅰ類應用模式下的適應度函數模型:

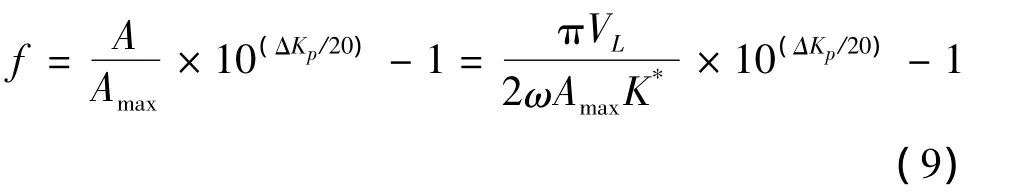
設置CTGDDE算法的參數 T=30，M=60，q=0.2，η=0.1，C=0.9，假設攝動參數在標稱值上下15%范圍內浮動，運用Matlab編程迭代搜索8次即可使適應度函數的最小值穩定至f=2.0205＞0。圖5給出了算法的尋優曲線。由圖5可知，該系統滿足準則要求。此時 ΔKp=29.8339 dB，ω=16.5 rad/s，K*=0.9778，適應度函數最小值對應的最差狀態下的Nichols曲線見圖4。圖4中，最差狀態處的增益為 －27.8 dB，相位為 －168°，頻率為16.5 rad/s。

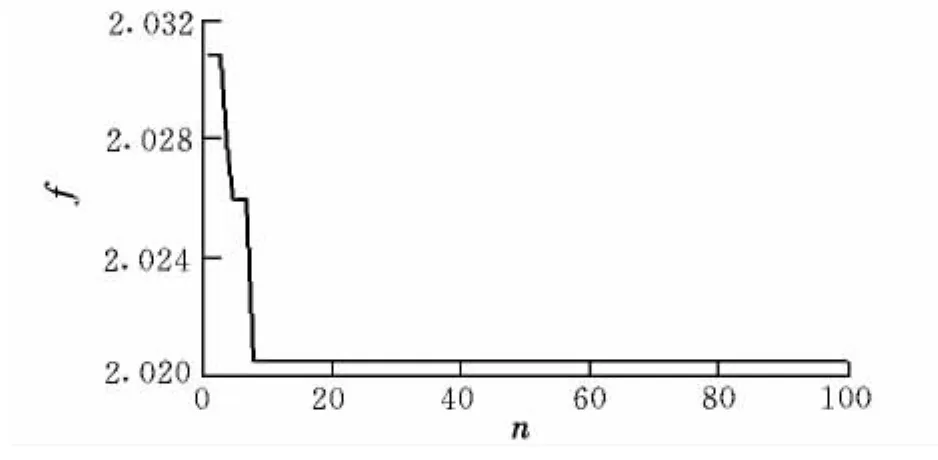
圖5 CTGDDE算法尋優曲線圖Fig.5 Optimization curve of CTGDDE algorithm

5 結束語

傳統的人機系統穩定性評估通常根據評估準則對飛行包線內設計點處的情況進行確認，而設計點間的情況只能借助于復雜的仿真運算，而且難以應對多參數同時變化的情況。針對上述不足，本文以控制系統中速率限制因素為例，建立相應的人機閉環系統模型，進而根據Gap準則利用CTGDDE算法對該情況下的人機PIO進行評估。該項研究為飛機研發階段PIO預測提供了一種新型高效的評估方法。

［1］ Liebst B S.Nonlinear pre-filter to prevent pilot-induced oscillations due to actuator rate limiting［J］.Journal of Guidance，Control，and Dynamics，2002，25(4):740-747.

［2］ 陳云翔，李琳，李千，等.基于改進差分進化算法的飛行控制律評估方法［J］.航空學報，2013，34(6):1261-1268.

［3］ 胡新江，胡浩軍，李大偉，等.速率限制舵機描述函數模型研究［J］.飛行力學，2011，29(5):14-17.

［4］ Ashkenas I L，Jex H R，McRuer D T.Pilot-induced oscillations:their causes and analysis［R］.Northrop-Norair Report，1964.

［5］ Hanke D.Handling qualities analysis on rate limiting elements in flight control systems［R］.Europe:AGARDAR-335，1995.

［6］ 孟捷，徐浩軍，張建康，等.Gap準則在II型PIO預測中的應用［J］.北京航空航天大學學報，2010，9(4):1067-1070.