關于單形穩定性的幾何不等式的改進

陳 士 龍

(安徽廣播影視職業技術學院 基礎教學部，安徽 合肥 230011)

0 引言

幾何不等式的穩定性也稱為穩定性版本，這個概念在上世紀80年代后才得到系統研究，其理論和方法被廣泛應用體視學、機器人中的幾何探索和仿晶學等領域.文獻［1－5］中對幾何不等式的穩定性概念給出了準確的描述.即指在一些含有等號的幾何不等式中，當其中的幾何體為某種特殊的幾何體或其中幾何體相似時取等號.假設某幾何體使得不等式與相等時相差很小，那么此幾何體與去等號的特殊幾何體的“偏差”也很小.比如在平面上凸體K 的等周不等式

當且僅當凸體K 為圓時取等號.其中P(K)與A(K)分別為凸體K 的周長與面積.假設對ε＞0，如果

能否斷定存在圓B，使得在某種“偏差”度量g(K，B)下，有

這里f(ε)是滿足當ε→0 時，f(ε)→0 的非負實函數.若存在某種“偏差”度量，使得當(2)成立時必有式(3)成立，則稱式(1)是穩定的，否則是不穩定的.

在不等式(1)中，存在圓盤B，K 與B 間的Hausdorff 度量為δ(K，B)，使得對任給實數ε＞0，當

時，有

若在(2)式中，令ε=(P(K))2－4πA(K)，便得到(1)式的一種加強形式

此時把不等式(5)稱為不等式(1)的一個穩定性版本.

設n 維歐氏空間En中的n 維單形Ωn的頂點集為{A1，A2，…，An+1}，它的棱長為aij=|AiAj|(1≤i＜j≤n+1)，有時也用表示單形的各個棱長，V 表示單形的體積，R 和r 分別表示n 維單形Ωn的外接球半徑和內切球半徑，Fi(i=1，2，…，n+1)表示單形頂點Ai所對的側面(n－1 維單形)的n－1維體積(面積).

設K 為n 維歐氏空間En中的有界凸體，對En中每個單位向量μ，凸體K 的一對與μ 垂直的支撐超平面之間的距離記為τ(K，μ)，令

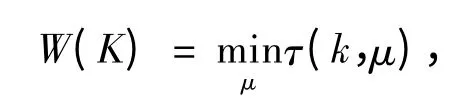
稱W(K)為凸體K 的寬度［6］.

Sallee 與1974年提出這樣的一個猜想:內接已知超球面的所有單形中，正則單形具有最大的寬度.Alexander 于1977年證明了這一個猜想，獲得如下的定量結果［6］:

在En中，n 維單形Ωn的寬度W(Ωn)與外接球面半徑R 之間成立不等式

當Ωn為正則單形時等號成立，其中

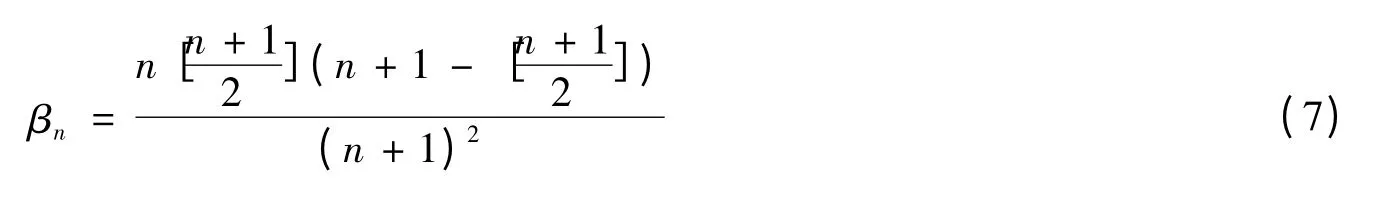
n 維單形Ωn的寬度W(Ωn)與體積V 之間成立不等式

當單形Ωn為正則單形時等號成立.上式即為著名的單形寬度的楊－張不等式.

1 主要結果

定理 設n 維單形Ωn的(n－1)－偏正度量為，則對任意的ε＞0，當

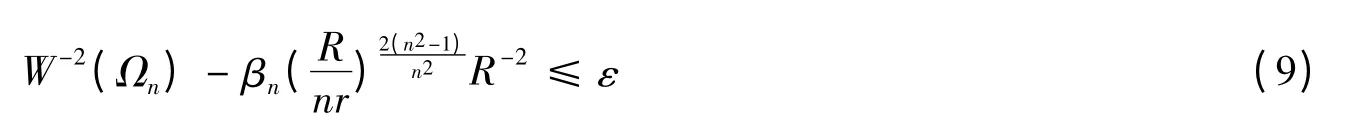
時，有

或不等式(6)的一個穩定性版本

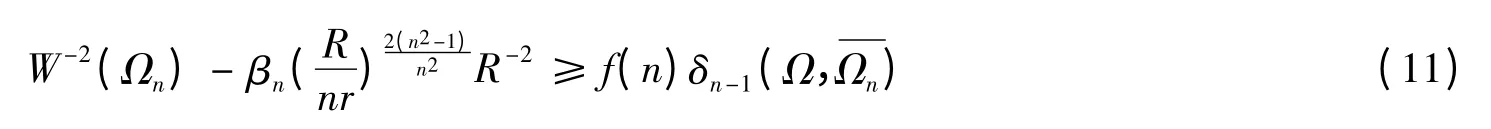
顯然不等式(10)是對不等式(6)的一種推廣.其中，

2 引理及引理的證明

為了證明上節中的幾個定理，需要引用下面幾個引理和定義，

定義1［8］設n 維歐氏空間En中n 維單形Ωn的棱長為是棱長為的正則單形，則單形Ωn的“偏正”度量定義為

更一般的，可對上面的定義進行推廣，則n 維單形Ωn的“k－偏正”度量為

其中Vi(k)(i=1，2，…，μn，k)是單形Ωn的k 維子單形的k 維體積

引理1［7］對n 維歐氏空間En中n 維單形Ωn的頂點集A={A1，A2，…，An+1}的每個非空真子集S，En中必存在一定向超平面H，使SAH，且A 中各點到H 的帶號距離都相等，若以v 表示H 的單位法向量，這個帶號距離就是τ(Ωn，v).令I={1，2，…，n+1}，θm表示I 的一切m 元子集所組成的集合，即:θm={σ|σI，|σ|=m}于是單形Ωn的頂點集A 的每一個子集Aσ，可以和I 的一個子集σ 對應Aσ={Sσ|α ∈σ，σI}，當1≤|σ|≤n 時，由引理1 可知存在定向超平面Hσ，使得Aσ中的一切點到Hσ的帶號距離都相等，若以vσ表示Hσ的單位法向量，記

引理2［7］對n 維歐氏空間En中n 維單形Ωn，有

引理3［7］對n 維歐氏空間En中n 維單形Ωn，記，則

引理4［9］對n 維歐氏空間En中n 維單形Ωn，有

等號成立當且僅當n 維單形Ωn維正則單形.

定理的證明:對一切σ ∈θm，計算的算術平均值為，由引理3 得，

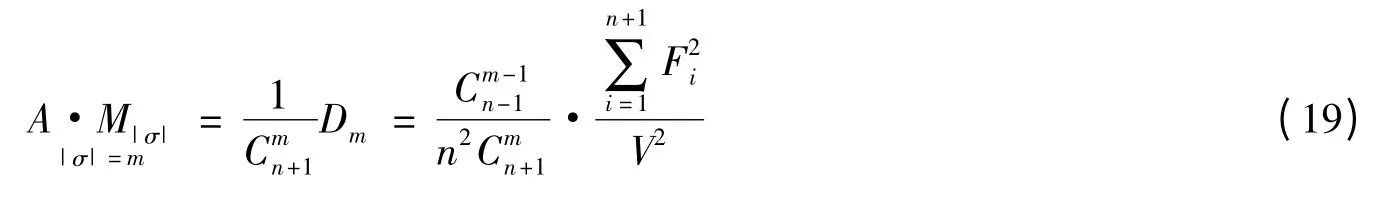
由單形寬度的定義可知

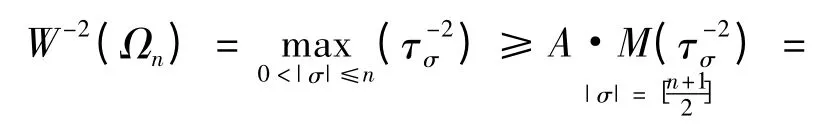
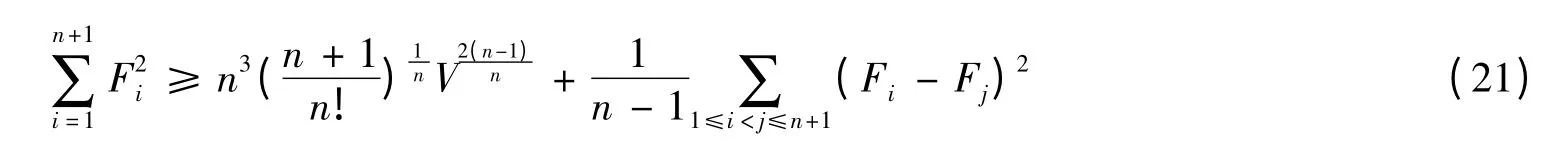
由不等式(20)和(21)得

由代數恒等式

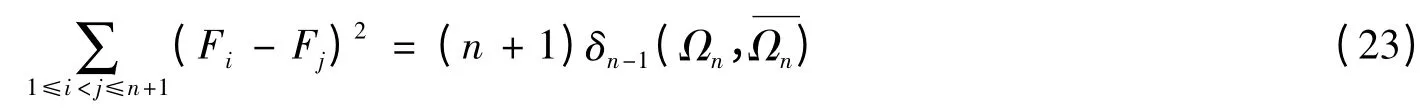
結合不等式(18)、(22)、(23)可得式(10).由推導過程可知當且僅當n 維單形Ωn為正則單形時等號成立.

由著名的Euler 不等式R≥nr 知，式(11)推廣了文［11］中的結論:在定理的條件下，成立

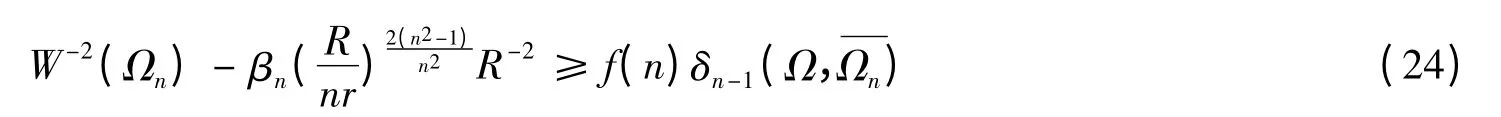
其中:

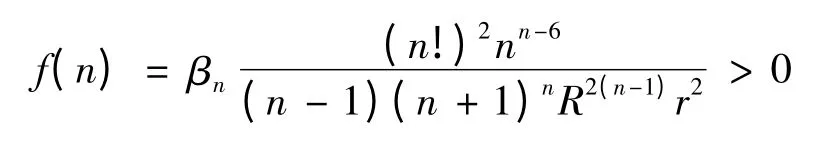
［1］Minkowski H.Volume und oberflache［J］.Math.Ann.，1903，57:447－495.

［2］Bonnesen.Probl emes des Isop im de Piphanes［M］.Paris:Gauthier－Villars，1929.

［3］Goodey P R，Groemer H.Stability results for first order projection bodies［J］.Poc.Amer.Math.Soc.，1990，109:1103－1114.

［4］Gardner R J，Vaddallo S.Stability inequalities in the dual Brun－Minkowski theory［J］.J.Math.Anal.and Appl.，1999，231:568－587.

［5］Grmer H.Stability properties of geometric inequalities［J］.Amer.Math，Monthly，1990，97:382－394.

［6］Alexander R.The width and diameter of a simplex［J］.Geometriate Dedicata，1997，6(1):87－94

［7］楊路，張景中.度量方程應用于Sallee 猜想［J］.數學學報，1983，26(4):488－493.

［8］馬統一.Veljan－Korchmaros’不等式的穩定性［J］.數學年刊，2008，29A(3):399－412.

［9］楊世國.關于內接單形的一個幾何不等式［J］.數學雜志，2003，23(2):218－220.

［10］冷崗送，唐立華.再論Pedoe 不等式的高維推廣及應用［J］.數學學報，1997，40(1):14－21.

［11］楊世國，等.關于單形幾個幾何不等式的穩定性［J］.浙江大學學報，2012，39(1):12－17.