船體結構強度評估的非線性設計波法研究

崔兵兵，王 瑜，曹 健

（上海船舶研究設計院，上海 201203）

0 引 言

20世紀七十年代末以來，水動力載荷非線性計算理論成為業內的研究熱點。目前工程實用的非線性載荷計算方法大體上可以分為時域方法和頻域方法兩類。國內外學者對于非線性波浪載荷時域計算方法的研究較多[1-3]。頻域非線性方法方面，具有代表性的是Jensen和Pedersen[4]基于攝動原理所建立的二階理論。

船體瞬時濕表面的顯著變化可導致流體靜力和動力的非線性特性。這一非線性特征，一方面導致波浪載荷響應包含有高頻分量；另一方面會使其幅值發生明顯變化，波浪彎矩的中拱與中垂分量不再相等，非線性波浪誘導應力范圍加大。而設計波方法是目前進行船體結構評估的主要方法，因此計及設計波的非線性對于更加合理地評估船體結構安全性具有重要意義。

以某深水多功能水下工程船為例：采用DNV船級社開發的Wasim軟件（基于三維Rankine源方法的時域線性/非線性船體運動與載荷預報程序），計算獲得目標船卷管盤重心處三個方向線加速度的幅頻響應算子RAO（response amplitude operator）及長期預報值；確定設計波參數，并對此規則波按Wasim軟件中的非線性理論進行計算，獲得目標船時域下的非線性運動和載荷響應；編寫并使用接口程序將時域下非線性波浪載荷傳遞到Patran有限元模型上；使用MSC.Patran/Nastran軟件對于目標船卷管盤區域的結構強度進行評估。

1 非線性設計波各要素確定方法

在采用非線性設計波法進行船體結構強度的評估時，非線性設計波各要素的確定是關鍵。非線性理論下設計波各個要素的確定方法一般說來有兩種[5]：

1) 嚴格法：從一開始便采用非線性波浪載荷理論，通過時域計算和取樣、擬合，分別求出中拱及中垂時運動和載荷響應的長期概率分布，進而得到中拱及中垂時的設計值；

2) 近似法：先采用線性理論，利用譜分析方法求得中拱與中垂運動和載荷響應的平均設計值，再根據不同航向角下算得的最大幅頻響應，將問題轉化為在響應最大的航向角（例如對于垂向波浪剪力與彎矩來說，就是迎浪）內的一個相當規則波，最后對此規則波按非線性理論進行計算，從而把中拱與中垂響應分離。該方法以其簡便易操作的特點，在工程實際中獲得廣泛應用。

2 設計波參數確定方法

設計波各要素的確定流程見圖1。設計波參數通常可按以下步驟確定：

1) 分析待評估部位的受力情況，確定運動或載荷控制參數；

2) 基于譜分析方法計算獲得選定的控制參數的幅頻響應；

3) 結合海浪譜和海況資料計算控制參數長期分布，得到對應一定概率水平的長期值；

4) 確定設計波參數，使待評估部位產生與長期預報值相當的控制參數響應值。

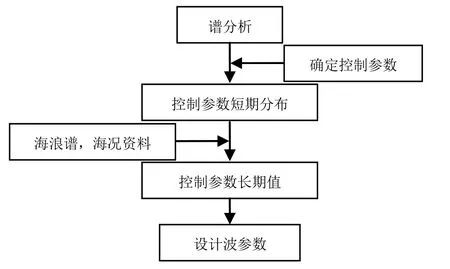
圖1 確定設計波各要素的流程

2.1 幅頻響應函數計算

幅頻響應函數H(ω)指的是船舶在單位波幅規則波中的各控制載荷參數的響應（如加速度，水動壓力，剖面載荷等）對應波浪頻率的傳遞函數，可用三維波浪載荷計算程序得到。

在實際的計算中，浪向角的范圍一般選取 0～330°以 30°為步長遞增，波浪頻率選取 0.1～2.0rad/s以0.1rad/s為間隔。

2.2 控制參數長期分布預報

求解獲得幅頻響應傳遞函數后，結合具體的波浪譜和海況散布圖就可以進行控制參數長期分布預報。

波浪譜一般采用ISSC（國際船舶結構會議）推薦的雙參數P-M譜（Pierson-Moschowitz譜），其表達式如下：

式中：Hs——有義波高，m；Tz——平均過零周期，s；ω——波浪圓頻率，rad/s；S(ω)——波浪譜密度函數，m2·s。

由傳遞函數H(ω)和波浪譜密度函數S(ω)，可以通過下式計算得到功率譜密度函數：

考慮到短期海況下波浪運動為平穩窄帶過程這一假設，對于船波構成的線性系統，控制參數的交變響應的峰值服從Rayleigh分布，概率密度函數為：

式中：R——控制參數響應峰值；m0——功率譜密度函數GXX(ω)的零階矩。

進而，可得到控制參數響應峰值的分布函數：

為得到控制參數在給定時間內的循環次數，需要給出控制參數交變響應過程的平均跨零率v，即單位時間內以正斜率跨越零均值的平均次數，其表達式為：

在計算控制參數響應平均跨零率時還要用到功率譜密度函數的2階矩。

控制參數功率譜密度函數GXX(ω)的n階矩計算通式為：

選定的海況分布資料，可獲得海況出現的概率。對于某一給定海況，船舶可能以任意航向航行，計算中可劃分nH個航向，并假定各個航向出現的概率相等。應力范圍的長期分布可表示為各短期分布的加權組合，其分布函數為：

式中：nS——海況分布資料中的海況總數；nH——劃分的航向總數；pi——第i個海況出現的概率，取為海況分布資料中各海況出現的頻率；pj——第j個航向出現的頻率；vij——海況i和航向j下，控制參數的平均過零率，由式(5)計算。

2.3 設計波參數確定

分析控制參數的幅頻響應計算結果，并在浪向和頻率范圍內進行搜索，獲得幅頻響應最大時對應的浪向、頻率及初相位，便為由該控制載荷參數出發得到的設計波要素（浪向β、頻率ω及初相位φ）。

通過式(7)可計算得到對應于一定超越概率的控制載荷參數長期值RL，通過搜索可獲得幅頻響應傳遞函數最大值RM，這樣對應的設計波的波幅[6]為：

3 實船分析

以某深水多功能水下工程船為例，依照“2”的方法確定設計波參數，應用Wasim軟件中的線性/非線性理論計算該設計波作用下船體波浪載荷和運動響應，按照船體結構強度評估流程，對于其卷管盤區域的船體局部結構強度進行評估。

3.1 有限元模型

采用MSC.Patran軟件建立了目標船艙段有限元模型（含卷管盤艙，月池等區域），目標船的主尺度及船型參數見表1，艙段有限元模型見圖2。

表1 目標船主尺度及船型參數 單位：m

3.2 設計波參數

選取 Wasim這一波浪載荷計算軟件進行目標船全船線性非線性水動力計算。目標船的水動力模型見圖3。計算參數設置見表2。

圖2 艙段有限元模型

圖3 目標船水動力模型

表2 Wasim軟件計算參數位置

3.2.1 幅頻響應函數計算

以卷管盤區域的局部強度評估為例。該處主要受到卷管盤慣性力載荷作用，因而選取目標船卷管盤重心處（見圖4）的縱向、橫向和垂向加速度值為控制參數。采用Wasim軟件計算獲得“2.1”所述單位規則波下選定控制參數的時歷響應，而后將其通過傅利葉轉換（Wasim軟件自帶模塊）得到控制參數的幅頻響應函數，結果見圖5～7所示。

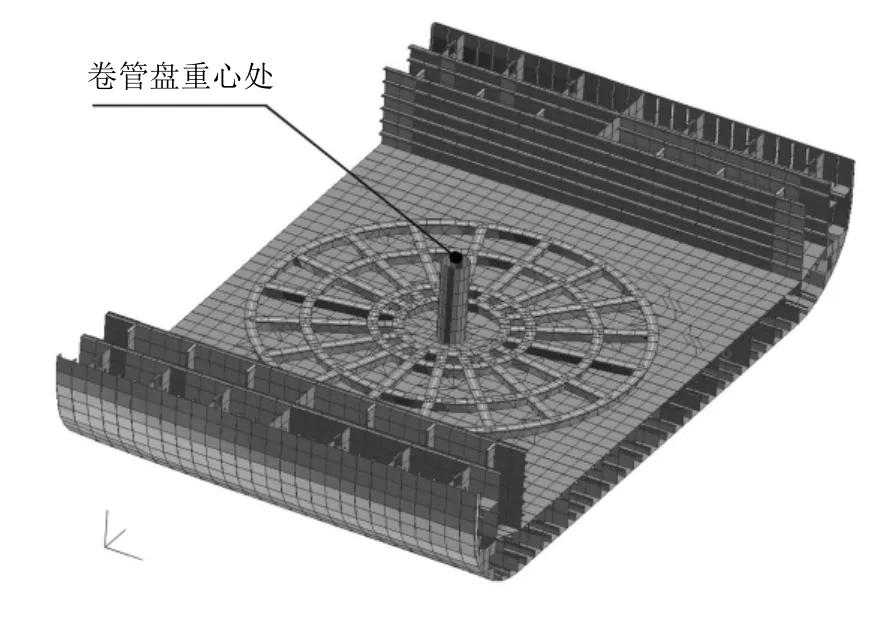
圖4 運動計算參考點位置

圖5 縱向加速度（Ax）傳遞函數

圖6 橫向加速度（Ay）傳遞函數

圖7 垂向加速度（Az）傳遞函數

3.2.2 控制參數長期分布預報

采用DNV船級社推出的Postresp后處理軟件，計算獲得目標船卷管盤重心處3個方向加速度的長期值，其計算參數選取：1) 海浪譜采用雙參數P-M譜；b) 海況選取北大西洋海況；3) 浪向等概率出現均為1/12；4) 超越概率水平選取10-8。計算獲得的目標船卷管盤重心處3個方向加速度的長期值（見表3）。

表3 長期值計算結果 單位：m/s2

3.2.3 設計波參數確定

依照“2.3”確定設計波參數的方法，確定的設計波見表4。

表4 設計波參數確定

3.3 船體結構強度評估

采用Wasim軟件非線性理論計算14kn航速下，線性/非線性設計波中船體的運動和載荷響應，計算時長取為1800s，時間步長0.1s。

該軟件所考慮的非線性因素[7]：1) 計及船體瞬時濕表面變化；2) Bernoulli方程中的速度平方項；3) 二階橫搖阻尼項。

通過計算可獲得考慮設計波的非線性條件下目標船重心及卷管盤重心處的加速度、端面處的彎矩和剪力、船體濕表面上的壓力響應時歷，作為后續船體結構強度評估的載荷輸入。同理選擇Wasim軟件的線性計算模塊，可計算獲得設計波線性理論下的載荷輸入。

3.3.1 模型靜力平衡與邊界條件選取

船體結構有限元模型通過分布質量點滿足靜水中的平衡條件（浮心與重心的縱向坐標之差為0.33m不超過船長的0.1%；排水量與規定的船舶重量之差為43.64t不超過排水量的0.5%）。目標船艙段模型兩個端面獨立點P1、P2（見圖8）處邊界條件[8]見表5。

圖8 端面邊界條件

表5 施加邊界條件

3.3.2 計算載荷施加

某一瞬時時刻，目標船艙段模型計算載荷的施加方式：1) 目標船全船的慣性力以在重心處建立加速度場的形式施加；2) 卷管盤的慣性力以力的形式施加到其重心處，并以Mpc的形式關聯到基座上；3) 端面所受的總體彎矩施加到端面的獨立點P1、P2上；4) 編寫并使用接口程序，將壓力計算結果（靜水和波浪壓力）由wasim水動力網格傳遞到patran有限元網格上，并將其以壓力場的形式施加到船體有限元外殼上[9]。

3.3.3 結構強度計算結果

計算表4設計波Ax作用下，卷管盤區域結構線性和非線性理論下的應力響應時歷。水動力載荷的計算時長為1800s，時間步長為0.1s，在進行船體結構應力響應計算時，選取1200～1220s時間段內的計算載荷進行施加。

采用MSC.Nastran軟件進行船體結構有限元準靜態分析，分別計算獲得線性/非線性設計波下，目標船卷管盤區域結構單元中心點X方向和Y方向應力時歷計算結果見圖9，剪應力和相當應力時歷計算結果見圖10。

由于水動力網格和有限元網格的差異，而導致水動壓力傳遞過程中產生的誤差等原因，會使得邊界處有不平衡力的產生，而導致模型邊界處應力響應過大。然而由于分析區域距邊界較遠，故在本文中邊界條件對目標區域應力分布的影響不作考慮。

圖9 X方向和Y方向應力響應時歷曲線

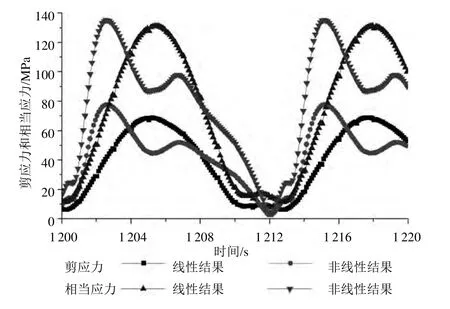
圖10 剪應力和相當應力響應時歷曲線

3.3.4 計算結果分析

通過對圖9和10中線性和非線性設計波下的應力響應時歷的比較可以看出：非線性設計波下的X方向主應力、剪應力和相當應力峰值明顯高于線性設計波；非線性設計波下Y方向主應力谷值明顯低于線性設計波。這也從側面證明了在進行船體結構強度評估時考慮載荷的非線性是十分必要的。

4 結 語

介紹了一種基于非線性設計波法的船體結構強度評估方法，并采用其計算獲得了某深水多功能水下工程船卷管盤區域結構的應力時歷響應，與線性設計波下的計算結果進行了比較。該研究證明了在進行船體結構強度評估時考慮載荷的非線性是十分必要的，并為采用非線性設計波方法的船舶結構設計提供了實例參考。

[1] Yamamoto Y, Fujino M, Fukasawa T. Motion and Longitudinal Strength of a Ship in Head Sea and the Effects of Non-linearities[J]. Naval Architecture and Ocean Engineering, JSNAJ, 1980,Vol.18.

[2] 陳超核，沈進威，徐秉漢. 規則波中船舶非線性波浪彎矩的時域計算[J]. 中國造船，1989(3).

[3] 段文洋. 船舶大幅運動非線性水動力研究[D]. 哈爾濱：哈爾濱工程大學博士論文，1995.

[4] Jensen, J.J. and Pedersen, P, T. Wave-induced Bending Moments in Ships-a Quadratic theory[J]. Trans. RINA, 1979, 2:151-165.

[5] 戴仰山，沈進威，宋競正，等. 船舶波浪載荷[M]. 北京: 國防工業出版社，2007.

[6] 劉冬平. 船體結構疲勞強度評估非線性設計波法[D]. 哈爾濱：哈爾濱工程大學，2012.

[7] 挪威船級社（Det Norske Veritas）. Sesam User’s Manual-Wasim [M]. 2014.

[8] 中國船級社（China Classification Society）. 油船結構直接計算分析指南[S]. 2003.

[9] 馮國慶，崔兵兵，任慧龍，等. 水動力網格至結構網格的壓力傳遞算法研究[A]. 船舶力學會議論文集[C]，西安：2013.