整函數(shù)及其微分多項(xiàng)式權(quán)分擔(dān)值

甘 媛

(福建船政交通職業(yè)學(xué)院公共教學(xué)部，福建福州350007)

1 相關(guān)知識(shí)

近年來(lái)，Lahiri與Banerjee引進(jìn)了一種權(quán)分擔(dān)的方法討論了亞純函數(shù)及微分多項(xiàng)式的唯一性問(wèn)題，這種方法極大地改進(jìn)了IM及CM思想.根據(jù)權(quán)分擔(dān)思想，本文完整的討論了(fn)(k)與(gn)(k)權(quán)分擔(dān)1值問(wèn)題，得到以下結(jié)果.

定理1.1:若f，g為兩個(gè)非常數(shù)整函數(shù)，正整數(shù)n，k滿足n ＞5k+7.如果(fn)(k)與(gn)(k)分擔(dān)(1，0)，則f=c1ecz，g= c2e-cz或 者 f= tg;其 中 c，c1，c2，t 為 滿 足(-1)k(c1c2)n(nc)2k=1及tn=1的常數(shù).

定義 1.1:設(shè) f，g(1，0)分擔(dān)，z0為f的q重1- 值點(diǎn)，定義為f，g公共1-值點(diǎn)且p=q=1時(shí)的計(jì)數(shù)函數(shù)為f，g公共1-值點(diǎn)且p＞q時(shí)的計(jì)數(shù)函數(shù);為f，g公共1-值點(diǎn)且p=q≥2時(shí)的精簡(jiǎn)計(jì)數(shù)函數(shù);類似地有我們記為公共1-值點(diǎn)的精簡(jiǎn)計(jì)數(shù)函數(shù)，且滿足p＞q=k，類似地有

2 主要引理及其證明

為證明定理我們需要以下引理.

引理 2.1［1］:若 f為非常數(shù)整函數(shù)，k 為正整數(shù)，c 為非零有限復(fù)常數(shù)，那么

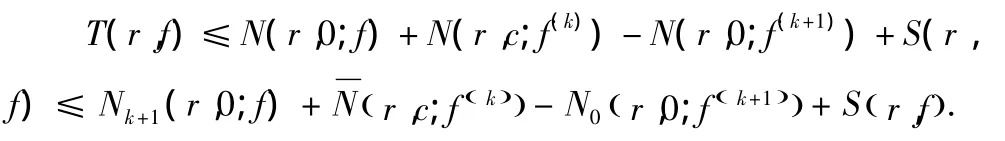
其中N0(r，0;f(k+1))為f(k+1)的零點(diǎn)但不是f(f(k)-c)的零點(diǎn)的計(jì)數(shù)函數(shù)的密指量.

引理 2.2［1］:若 f為非常數(shù)整函數(shù)，兩個(gè)亞純函數(shù) α1，α2滿足，那么

引理2.3:若f為非常數(shù)整函數(shù)，為k正整數(shù)，那么

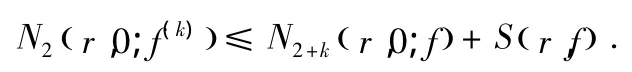
證明:由于 f為整函數(shù)及文獻(xiàn)［2］，有 N(r，0;f(k))≤N(r，0;f)+S(r，f).

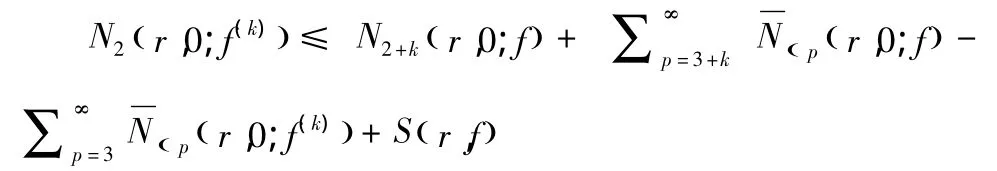
故引理2.3得證.

引理2.4［3］:若 f為非常數(shù)整函數(shù)，正整數(shù) k ≥ 2.如果ff(k)≠0，那么 f=eaz+b，這里 a≠0，b為復(fù)常數(shù).

引理 2.5［4］:如果兩個(gè)非常數(shù)整函數(shù) F，G 分擔(dān)(1，0)且滿足H≠0，那么

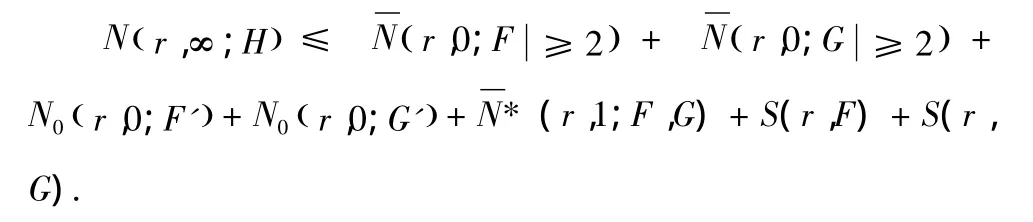
這里N0(r，0;F′)為F′的零點(diǎn)但又不是F(F-1)的零點(diǎn)的計(jì)數(shù)函數(shù)的精簡(jiǎn)密指量，類似地有N0(r，0;G′).

引理 2.6［5］:如果兩個(gè)非常數(shù)整函數(shù) F，G 分擔(dān)(1，0)且滿足H≠0，那么

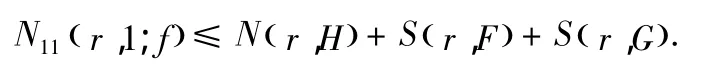
引理2.7:如果兩個(gè)整函數(shù)分擔(dān)，那么

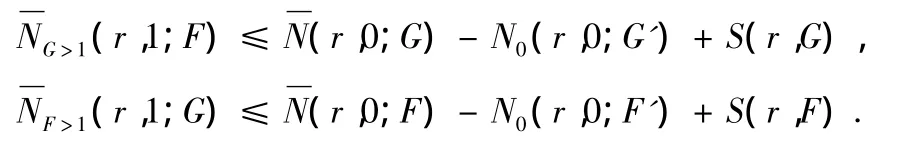
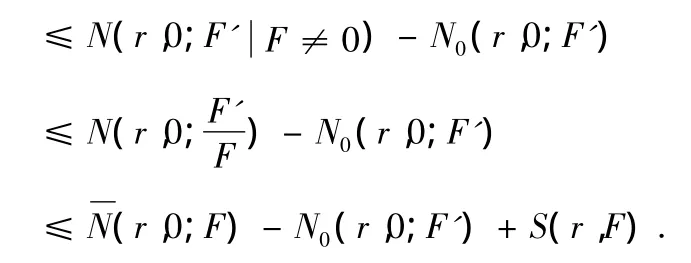
引理2.8:若兩個(gè)非常數(shù)整函數(shù)分擔(dān)，那么

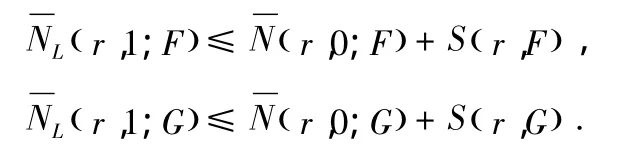
證明:由文獻(xiàn)［5－8］知

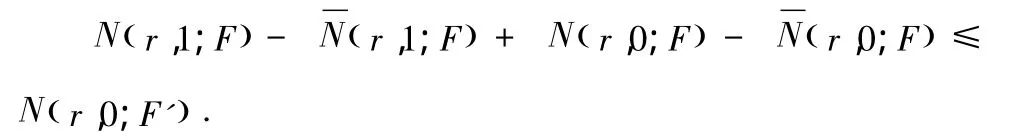
由 于 F，G 為 整 函 數(shù)，有 N(r，0;F′)≤ N(r，0;F)+S(r，F(xiàn)).

類似地可以得到引理中的第二個(gè)式子，這樣引理2.8得證.

引理2.9:若f，g為兩個(gè)非常數(shù)整函數(shù)，k為正整數(shù)，如果f(k)與g(k)分擔(dān)(1，l)，若 l=0，

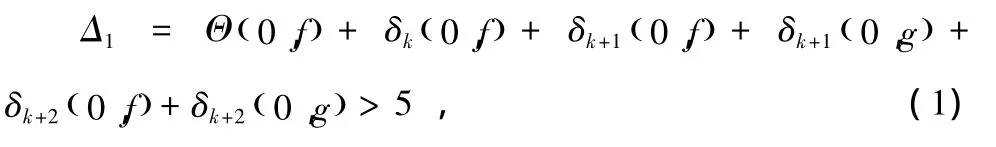
當(dāng)l=0，于是F，G分擔(dān)(1，0)，假設(shè)H≠0，那么得到

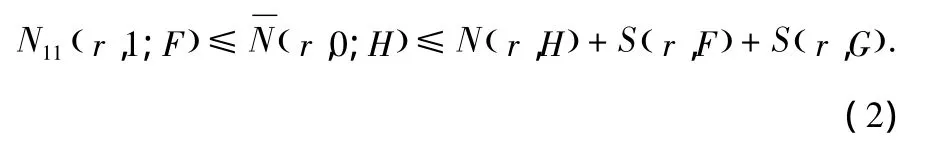
那么根據(jù)引理 2.5，2.6，2.7，2.8 及(2)式，有

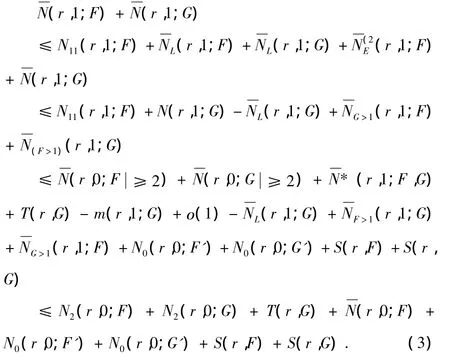
因?yàn)镕=f(k)及G=g(k)，

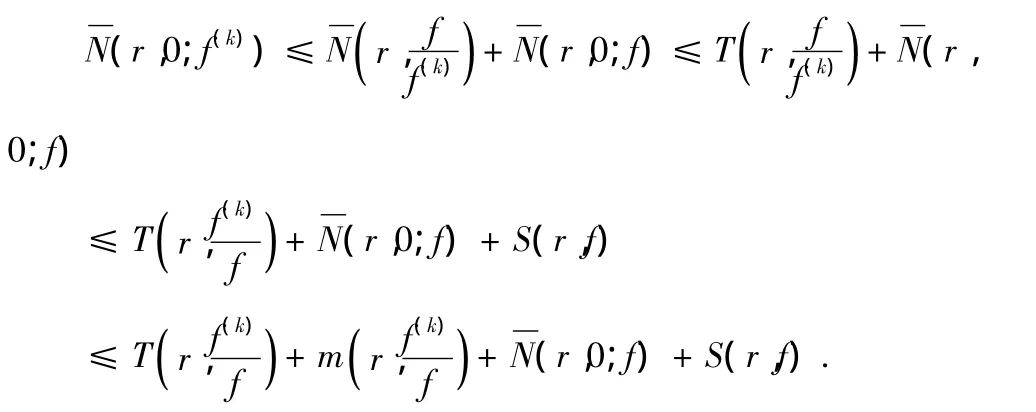
因此根據(jù)引理2.3，(3)式變?yōu)?/p>

再根據(jù)引理 2.1，有

這樣，由(2)—(6)，有

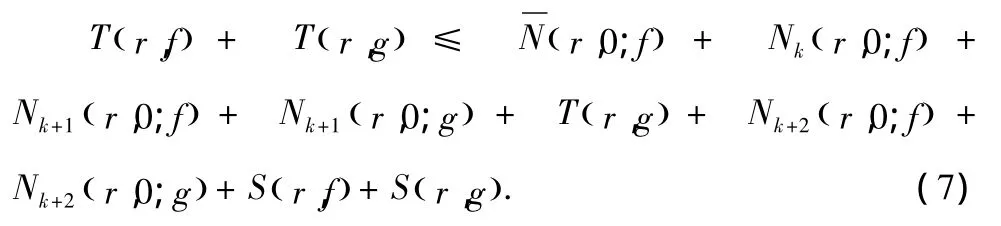
由(7)式有

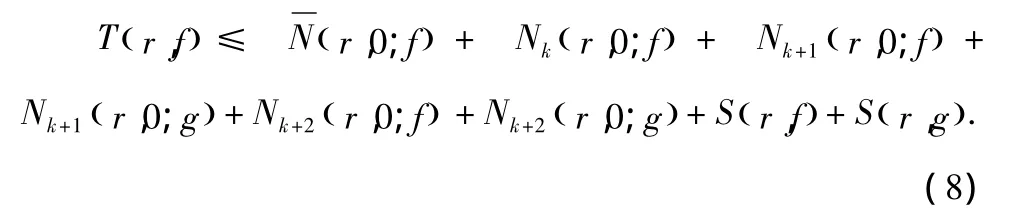
不妨設(shè)，存在一個(gè)具有無(wú)限測(cè)試的集合使得T(r，g)≤T(r，f)當(dāng) r∈I.因此

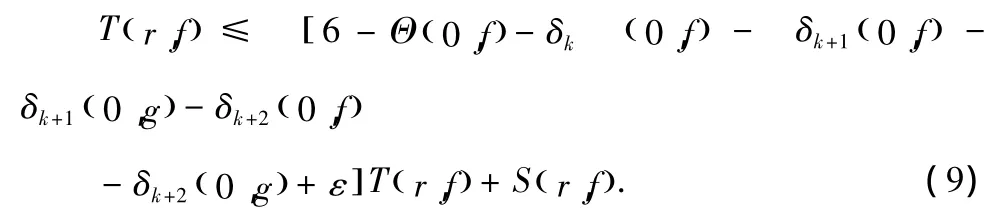
當(dāng) r∈ I及0 ＜ ε ＜ Δ1-5，于是{Δ1-5- ε}T(r，f)≤S(r，f)i.e.

Δ1-5≤0，

i.e.

Δ1≤5，

由Δ1＞5，這樣就產(chǎn)生了矛盾.

因此H≡0，那么

孫巖國(guó)舉例，在門診大廳掃描支付二維碼，輸入姓名、電話號(hào)碼和身份證號(hào)，選擇診室，頁(yè)面將迅速?gòu)棾鰭焯?hào)成功信息。就診后，醫(yī)囑的化驗(yàn)采血信息及時(shí)“導(dǎo)航”，顯示相關(guān)科室地點(diǎn)及距離。醫(yī)生開(kāi)藥次日早晨，提醒服藥的信息已發(fā)送至患者手機(jī)，“想忘記吃藥都難”。整個(gè)過(guò)程，省卻了排隊(duì)掛號(hào)、交費(fèi)的煩惱，也不再受找不到診室而困擾。“最重要的是開(kāi)通了住院預(yù)交金，一日清單、體驗(yàn)登記和報(bào)告書(shū)等移動(dòng)支付項(xiàng)目，醫(yī)保的二次結(jié)算也可順利實(shí)現(xiàn)。”

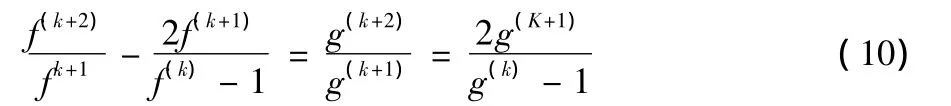
解上述微分方程得到

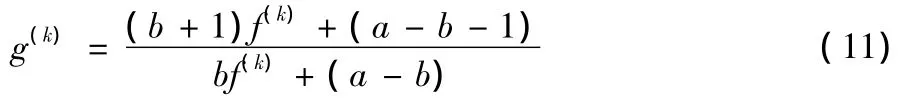
這里a(≠0)，b為兩個(gè)常數(shù).

接下來(lái)分三種情形討論.

情形1:b≠0，-1.若a-b-1≠0，由(11)有

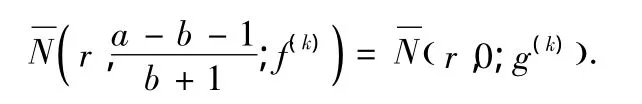
再根據(jù)引理2.1有

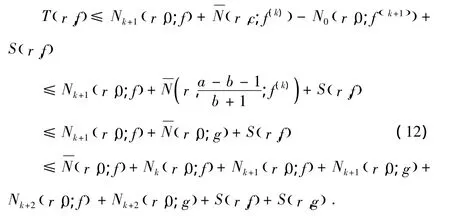
這樣由(1)，我們得到Tr，()f≤Sr，()f，r∈I，矛盾.

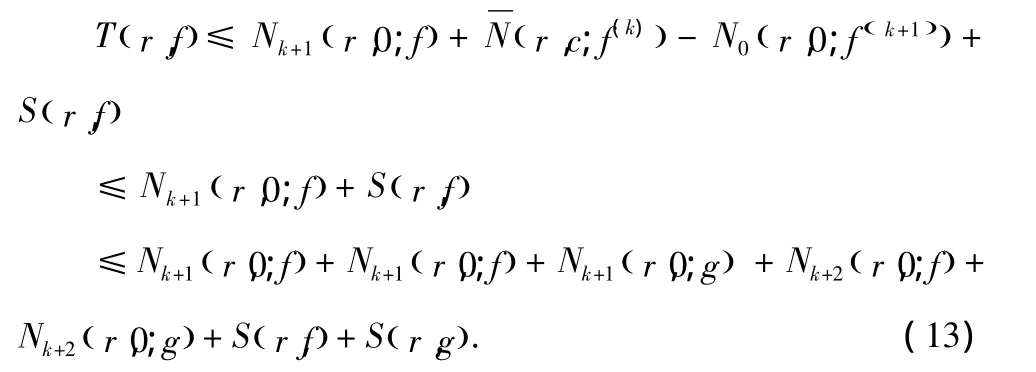
那么由(1)式得到 T(r，f)≤ S(r，f)，r∈ I，矛盾.

若a+1≠0，那么a+1為f(k)的一例外值.類似于情形1可得到矛盾.

若 a+1=0，那么 f(k)g(k)≡1.

情形3:b=0:由(11)式得到g(k)=(f(k)+a-1)/a.

若a-1=0，那么f(k)≡g(k).解此方程，有

f=g+p(z).

這里 p(z)為多項(xiàng)式.由上式有 T(r，f)=T(r，g)+S(r，f).

若 P(z)≠0，由引理 2.2，得到

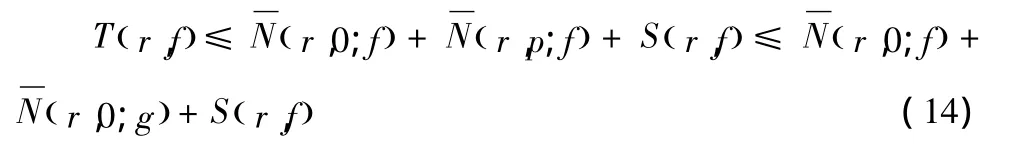
因此，可以得到

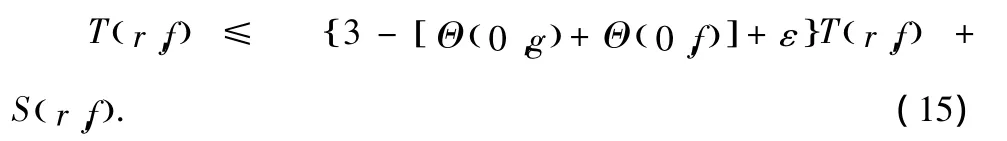
其中0＜ ε ＜1-δk+1(0，f)+1-δk+2(0，f)+1-δk+2(0，g).

于是有 {Δ1-5}T(r，f)≤ S(r，f).

因此由(1)，可得到 T(r，f)≤ S(r，f)，r∈ I，又一矛盾.

那么可知p(z)≡0，于是f≡g.

引理 2.10［2］:若 f1(z)，f2(z)，…，fn(z)為不同亞純函數(shù)以及g1(z)，g2(z)，…，gn(z)為整函數(shù)，滿足

(ii)當(dāng)時(shí)，為非常數(shù)，

那么 fj(z)≡0(j=1，2，…，n).

3 定理的證明

定理 1.1 的證明:令 F=fn，G=gn.這樣就有

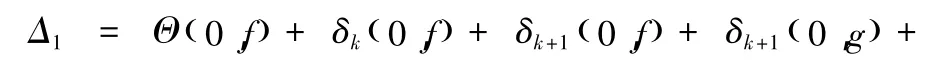
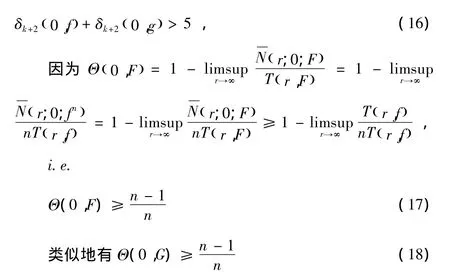
由Nk(r，a;f)的定義知

由(16)－(23)可以得到

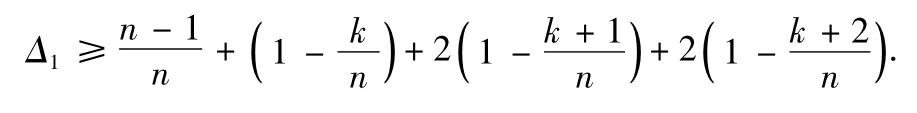
由于n＞5k+7可得Δ1＞5.

由于F(k)=(fn)(k)及G(k)=(gn)(k)，再根據(jù)定理1.1的條件知，F(xiàn)(k)，G(k)分擔(dān)(1，0)以及F，G滿足引理2.9的條件.

下面分兩種情形討論.

情形1:F(k)G(k)≡1;

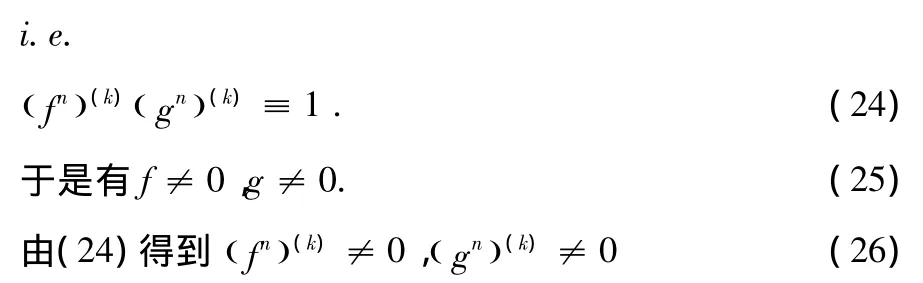
再根據(jù)(24)，(25)，(26)及引理2.4，當(dāng) k≥2 時(shí)，我們有，這 里 C1，C2，C3為 常 數(shù) 且 滿 足

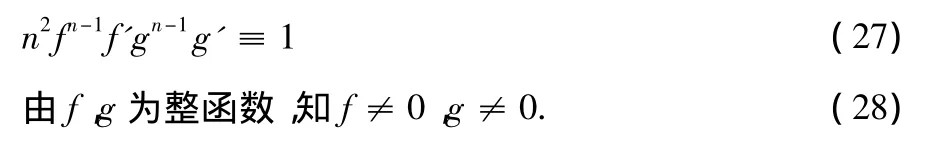
i.e.，n(eμ+eν)+ μ′+ ν′≡ 0.那么由(31)可得到

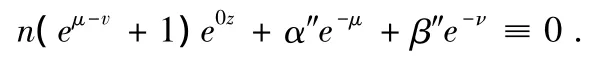
再根據(jù)引理 2.10，可得 eμ-ν+1=0，i.e.，eμ-ν=-1.于是

μ-ν=(2m+1)πi，對(duì)某個(gè)整數(shù)m，

i.e.，

μ =v+(2m+1)πi，對(duì)某個(gè)整數(shù)m.

將上式代入(32)得到μ′=ν′≡0，于是μ=ν為常數(shù)i.e.α′，β′也是常數(shù).

這樣由(26)－(31)，得到 f=c1ecz，g=c2e-cz，這里c1，c2.c為常數(shù)，滿足(-1)k(c1c2)n(nc)2k=1.

綜合以上過(guò)程知:若 F(k)G(k)=1，k≥1，有f=c1ecz，g=c2e-cz，這里 c1，c2，c為三常數(shù)，滿足(-1)k(c1c2)n(nc)2k=1.

情形 2:F≡G，i.e.fn≡gn.這時(shí)可得 f=tg，其中 tn=1.

綜合情形1與2，就可得到定理1.1.

［1］Hayman W K.Meromorphic Functions［M］.Oxford:The Clarendon Press，1964.

［2］Yang C，Yi H.Uniqueness theory of meromorphic functions［M］.Beijing:Science Press，1995.

［3］Frank G.Eine Vermutung von Hayman uber nullstellen meromorphic function［J］.Math Z，1976，149:29－36.

［4］Banerjee A.Meromorphic functions sharing one value［J］.Int J Math Sci，2005，(22):3587－3598.

［5］Lahiri I.Weighted value sharing and uniqueness of meromorphic functions［J］.Complex Variables Theory Appl，2001，(3):241－253.

［6］Lahiri I.Value distribution of certain differential polynomials［J］.Int J Math Sci，2001，28:91－93.

［7］Lahiri I.Weighted sharing and uniqueness of meromorphic functions［J］.Nagoya Math J，2001，161:193－206.

［8］Lahiri I，Sarker A.Uniqueness of a meromorphic functionand its derivative［J］.J Inequal Pure Appl Math，2004，(1):Article 20.