程度近似算子的復合運算研究
黃衛華,李艷艷,周 平
(文山學院數學學院,云南文山663000)
波蘭數學家Z.Pawlak于1982年首次提出粗糙集理論[1].Pawlak粗糙集理論是在等價關系上定義的上、下近似算子,具有一定的局限性,在實際應用中有許多方面的推廣,如基于一般關系的粗糙集模型[2-3]、基于鄰域算子的粗糙集模 型[4-6]、程 度 粗 糙 集 模 型[7-9]以 及 變 精 度 粗 糙 集 模型[10-13]等.
1 預備知識
定義1設是一個近似空間,假設X(X≠φ)?U,k為非負整數,定義X關于近似空間S依程度k的下近似和上近似分別為
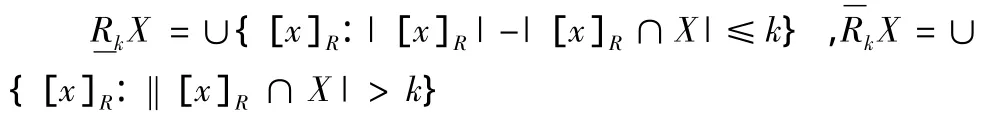
定義2設U是非空有限論域,?X?U,定義程度上、下近似算子的復合運算為引理1設S=(U,R)是一個近似空間,假設X,Y?U,k為非負整數,程度近似算子滿足下列性質:

2 主要結果
證明:由定義1與定理1易證.
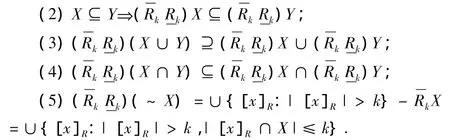
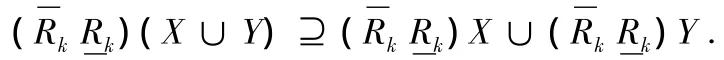
(4)證明類似(3).
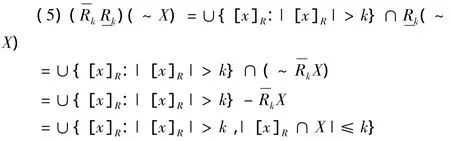
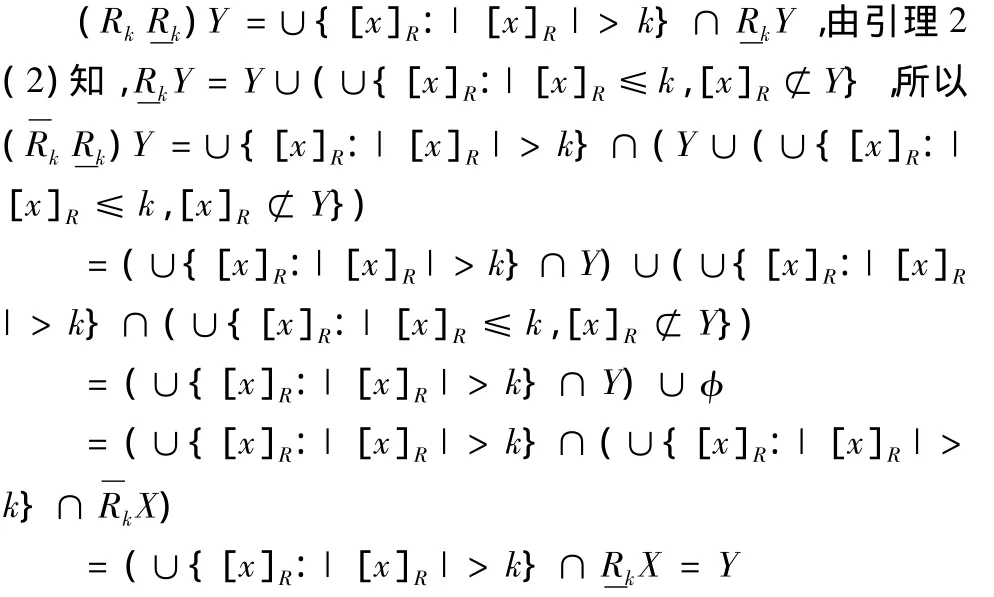
3 實例分析
設(U,R)為近似空間,其中 U={x1,x2,…,x20},[x]R={E1,E2,…,E5}為 R 的等價類構成的集合,E1={x1,x2,x3,x4,x5},E2={x6,x7,x8},E3={x9,x10,x11,x12},E4={x13,x14,x15,x16},E5={x17,x18},
令 X={x4,x5,x8,x14,x15,x16,x17,x18},k=2,則
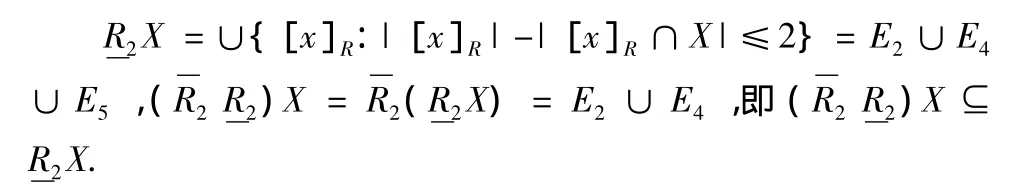
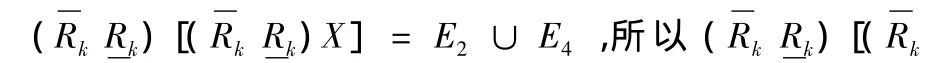
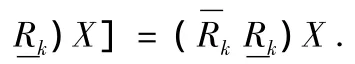
4 結論
本文在程度粗糙集中定義了程度上、下近似算子的復合運算,研究了復合運算的性質,并給予了嚴格的證明,最后通過一個實例驗證了定理的正確性,同時說明了所定義的程度上、下近似算子的復合運算具有冪等率.
[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,(5):341-356.
[2]顧力平,楊習貝.基于一般二元關系的多粒度粗糙集模型[J].南京航空航天大學學報,2013,(1):124-129.
[3]滕書華,魯敏,楊阿鋒等.基于一般二元關系的粗糙集加權不確定性度量[J].計算機科學,2014,(3):649-665.
[4]李三樂.基于鄰域粗糙集模型的屬性約簡算法改進[J].微計算機信息,2010,(12):268-270.
[5]王天擎,趙良輝,謝軍.區間值信息系統中基于鄰域系統的粗糙集模型[J].計算機應用研究,2012,(11):4242-4245.
[6]唐朝輝,陳玉明.鄰域系統的不確定性度量方法[J].控制與決策,2014,(4):691-695.
[7]吳志遠,鐘培華,胡建根.程度多粒度粗糙集[J].模糊系統與數學,2014,(3):165-172.
[8]張賢勇,謝壽才,莫智文.程度粗糙集[J].四川師范大學學報,2010,(1):12-16.
[9]張賢勇,莫智文.程度上、下近似算子的乘積運算[J].四川師范大學學報,2011,(6):775-779.
[10]Ziarko W.Variable precision rough set modle[J].J Computer and System Sciences,1993,46:39-59.
[11]許韋,吳陳,楊習貝.基于相似關系的變精度多粒度粗糙集模型[J].科學技術與工程,2013,(9):2517-2522.
[12]石夢婷,劉文奇,余高峰.變精度軟粗糙集[J].計算機工程與應用,2014,(1):101-104.
[13]閆敏倫.新型變精度多粒化粗糙集模型[J].南京理工大學學報,2014,(4):496-500.

