淺談“分數(shù)墻”在“異分母加減法”教學(xué)中的應(yīng)用

浙江湖州市鳳凰小學(xué)（313000） 呂 莉

淺談“分數(shù)墻”在“異分母加減法”教學(xué)中的應(yīng)用

浙江湖州市鳳凰小學(xué)（313000） 呂 莉

數(shù)學(xué)教學(xué)中，直觀具體的模型對于學(xué)生理解和記憶所學(xué)知識有非常大的幫助。利用“分數(shù)墻”的教學(xué)，可以直觀地將分數(shù)的大小比較和分數(shù)的加減計算知識進行復(fù)習(xí)，同時形象地再現(xiàn)相等分數(shù)，引導(dǎo)學(xué)生作直觀的探究，使學(xué)生對等價類分數(shù)有更深刻的認識。

分數(shù)墻 課堂教學(xué) 教學(xué)效果 算理 分數(shù)

“分數(shù)墻”是人教版修訂稿教材中經(jīng)常出現(xiàn)的學(xué)習(xí)材料，它在分數(shù)的初步認識、分數(shù)的大小比較、分數(shù)單位、分數(shù)的加減法運算、分數(shù)乘除法運算等教學(xué)中都可以應(yīng)用。在教學(xué)中，“分數(shù)墻”的引入能使學(xué)生理解運算的算理，以直觀的形式告訴學(xué)生“為什么可以這么計算”。如在“異分母分數(shù)加減法”一課教學(xué)中，我就應(yīng)用“分數(shù)墻”展開教學(xué)，取得了很好的教學(xué)效果。

一、借助“分數(shù)墻”溫習(xí)同分母分數(shù)加減的算理

師（課件出示分數(shù)墻，如右圖）：你看到了哪些分數(shù)？

師：請選兩個分數(shù)，組成同分母分數(shù)加減法的算式。

生1

師：你是怎么算的？

生：分子相加，分母不變。

師（小結(jié)）：分數(shù)單位相同的分數(shù)可以直接相加減。

……

在上述教學(xué)中，從“分數(shù)墻”開始，讓學(xué)生尋找分數(shù)并組成加減法算式。學(xué)生通過對“分數(shù)墻”的觀察，得到諸多的同分母分數(shù)加減法算式，進一步明確同分母加減法的計算算理和計算方法。

二、借助“分數(shù)墻”明晰異分母分數(shù)加減的算理

討論A：這樣算對嗎？為什么？（如右圖，移動兩個加數(shù)部分的顏色，對比和）

討論B：為什么分母不同就不能直接相加？

生：分數(shù)單位不同。

討論C：為什么分數(shù)單位不同不能直接相加？（“分數(shù)墻”上每一塊的大小不同通過多媒體，閃動小塊）

討論A：為什么要把這兩個分數(shù)轉(zhuǎn)化成分母是10的分數(shù)？

生：分數(shù)單位相同。

討論B：你怎么想到要轉(zhuǎn)化成分母是10的分數(shù)？（如右圖，“分數(shù)墻”移動加數(shù)部分的色塊，的色塊移動到……）

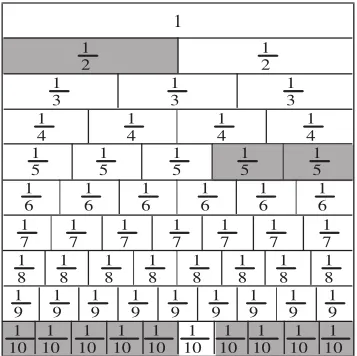
討論C：分母通分時，用什么數(shù)當公分母？

生：2和5的公倍數(shù)。

討論D：你覺得選擇哪個數(shù)當公分母更方便？

生：最小公倍數(shù)。

討論：0．5和0．4相加，為什么等于0．9？

生：5個0．1加4個0．1等于9個0．1。（在分數(shù)墻上找到0．5和0．4）

師：對比化成小數(shù)和化成同分母分數(shù)兩種方法，它們有沒有相同點？

生：它們都先轉(zhuǎn)化成了相同的計數(shù)單位，統(tǒng)一了計數(shù)單位。

師（引導(dǎo)學(xué)生對比錯例后總結(jié)）：計數(shù)單位不同，不能直接相加。

……

“分數(shù)墻”既可以為同分母分數(shù)加減法計算算理提供圖像表征，又可以圖像表征異分數(shù)單位不能直接相加減的算理，用圖形的大小排除錯誤的想法。在本環(huán)節(jié)的教學(xué)中，通過對比錯例與通分、通分與化小數(shù)的計算方法，應(yīng)用“分數(shù)墻”圖形表征三種算法的合理性，借助幾何直觀使學(xué)生明確計數(shù)單位相同才能相加減的算理。

三、借助“分數(shù)墻”感悟等價類分數(shù)的價值

整體觀察：

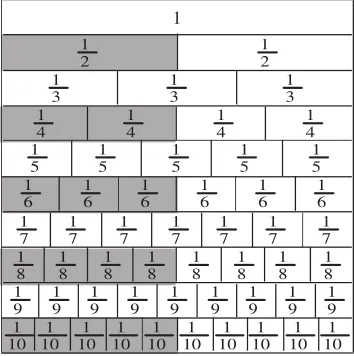
師：這組分數(shù)是相等的，就好比一個人有不同的裝束，如校服、運動服、休閑服、西裝等，在學(xué)校上課需要穿校服，運動時穿運動服，生活中穿休閑服，舞臺上穿西裝……但不管穿什么衣服，都是同一個人。

……

設(shè)計一系列的環(huán)節(jié)無非是讓學(xué)生知道“只有統(tǒng)一分數(shù)單位才能相加減”，這其實就是等價類不同形態(tài)分數(shù)存在的價值，如能在教學(xué)中增加這一提煉環(huán)節(jié)，學(xué)生會對等價類分數(shù)有更深刻的認識。教師的比喻盡管不能完全準確，卻讓學(xué)生體會到數(shù)學(xué)的原始思想其實也很平常，更易使學(xué)生理解所學(xué)知識。

（責(zé)編 藍 天）

G623.5

A

1007-9068（2015）23-046