多智能體協同尋優的主動配網動態拓撲重構

董如良，楊 強，顏文俊

（浙江大學電氣工程學院，浙江杭州310027）

多智能體協同尋優的主動配網動態拓撲重構

董如良，楊 強，顏文俊

（浙江大學電氣工程學院，浙江杭州310027）

針對當前含有大量具有間歇性的分布式可再生電源接入的主動配電網，通過引入多智能體系統（MAS）思想，提出改進的拓撲重構方法和粒子群算法優化（PSO）協同尋優的多目標動態拓撲重構的算法設計.相對于已有的配電網拓撲重構解決方案，通過采用基于事件驅動的重構觸發機制，降低拓撲重構頻率以降低重構對配電網運行的負面影響，在重構算法設計中兼顧了經濟性和安全性指標優化的同時，降低了優化算法的復雜度.結合IEEE-33節點和美國PG＆amp；E 69節點2個典型算例，對該方法進行仿真實驗驗證.實驗結果表明，采用該方法能夠有效地計及隨機性以及不確定因素對配電網重構的影響，具有良好的計算效率和算法穩定性.

配電網；分布式電源；多智能體；粒子群；最短路算法；層次分析法（AHP）

目前應用于配電網拓撲重構的主要策略是人工智能與數值計算相結合的方法，包括遺傳算法[1-3]、模糊評估算法[4]、專家系統方法[5]、化學反應算法[6]等.

鑒于配電網絡運行過程中負荷狀態是動態變化的，研究計及負荷變化的動態重構問題更有實際意義.王成山等[7-9]認為，DG供電的隨機性對網絡運行狀態有很大的影響.其中王成山等[7]根據半步變量法的隨機潮流計算結果，得到了網絡運行參數；李傳健等[8]采用兩點估計法，考慮在風力隨機潮流的基礎上進行配電網重構，降低了系統網損，提高了系統穩定性；吳小珊等[9]考慮風電不確定性，將風電功率區間預測信息納入到日前計劃中.

多智能體系統（multi-agent system，MAS）中的代理通過競爭或協商等手段解決各代理成員目標和行為之間的矛盾與沖突[10].多Agent算法是一種通過多級智能體之間的通信協同優化的系統算法[11]，多Agent技術及其思想在電力系統中已有廣泛的應用[12-14].

配電網可以理解為在賦權圖中，所有負荷節點都須建立與根節點的連接路徑.李傳健等[15]將圖論算法中的最小生成樹應用在配電網重構中.

粒子群優化（particle swarm optimization，PSO）算法不能直接應用處理連續變量問題的基本粒子群算法.盧志剛等[16]將高斯分布和二進制PSO算法結合，結合禁忌搜索進行配電網重構；李振坤等[17]將二進制和離散PSO算法組合，得到一種混合PSO算法，實現配電網重構的離散問題優化.

層次分析法（analytic hierarchy process，AHP）應用于多目標決策可以處理難以完全定量分析的問題，它為相互關聯、相互制約的眾多因素的決策和排序提供了多準則決策方法.

綜上所述，粒子群算法自身不適合處理離散優化問題，基于圖論的算法存在盲目搜索和路徑權重難以確定的問題.針對上述問題，本文引入多智能體系統思想，提出基于多智能體協同尋優的主動配電網動態拓撲重構方法和算法設計.

1 多智能體的協同優化架構

本文的協同重構采用MAS的集中式體系結構，如圖1所示.

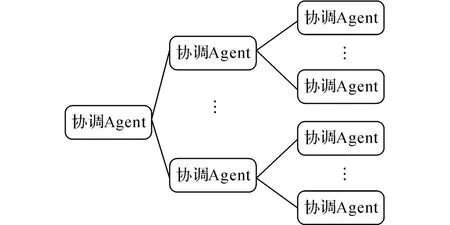
圖1 集中式體系結構圖Fig.1 Centralized architecture diagram

協同體系采用協調Agent、管理Agent和粒子Agent三級智能體協同尋優的重構機制，協調Agent負責協調整個重構過程.根據協調Agent的重構執行判斷模塊，判斷是否達到重構條件.若達到，則協調代理分配一個新的管理代理，管理N×N個粒子Agent完成一次新的重構，重構由管理Agent的優化計算模塊采用改進粒子群引導的最短路徑算法完成.

協調Agent有以下3個功能模塊.1）重構執行判斷模塊根據重構執行判斷條件，判斷是否進行一次新的重構.若達到，則給下一時段分配管理代理；若未達到，則繼續下一次判斷.重構執行判斷條件可以為任意合理的標準或事件，如配電網故障、網損過大、分布式電源出力波動過大以及節點電壓過低等.2）管理代理交互模塊接收管理代理匯報的信息，并向管理代理發送指令.3）最優解協調模塊.當初始最優解不滿足開關次數約束時，根據各個管理代理上報的替補解集，結合允許的開關次數執行最優解篩選，得到當次重構的最優解.

管理Agent有以下4個功能模塊.1）優化計算模塊采用改進粒子群引導的最短路徑算法求得初始解集.2）解集準備模塊結合目標函數，根據定義的排序機制確定解集中解的順序，形成替補解集.3）前驅代理交互模塊將前一時段的最優解加入到迭代初始種群中，完成第一次向前驅管理代理學習.若最優解集所有解的開關次數均越限，則將前一時段最優解作為當前時段最優解，這樣網絡結構保持不變，開關完全不動作，完成第二次向前驅代理學習的過程.4）協調代理交互模塊向協調代理匯報結果，接收協調代理的命令.

系統架構如圖2所示.

2 拓撲重構問題建模

配電網動態重構是在負荷不斷變化的情況下求解一段時間內的重構方案，一些多目標優化問題通過求取Pareto最優解完成多目標優化，但該類方法往往計算量大且耗時較長，不適合在線應用；可以采用對各種指標進行加權組合，如汲國強等[18]為了能夠考慮經濟性和安全性2個目標，將支路最大電流和支路阻抗進行加權組合，同時對2個目標進行優化，但該方法是單目標優化的尋優方式.本文選取以下3個目標函數進行優化.

1）網損.目標函數的表達式為

式中：Nb為支路總數；Pi和Qi分別為支路bi的有功功率和無功功率；Ri為支路bi的電阻；Ui為bi的首端電壓；ki為開關狀態變量，0表示打開，1表示閉合.

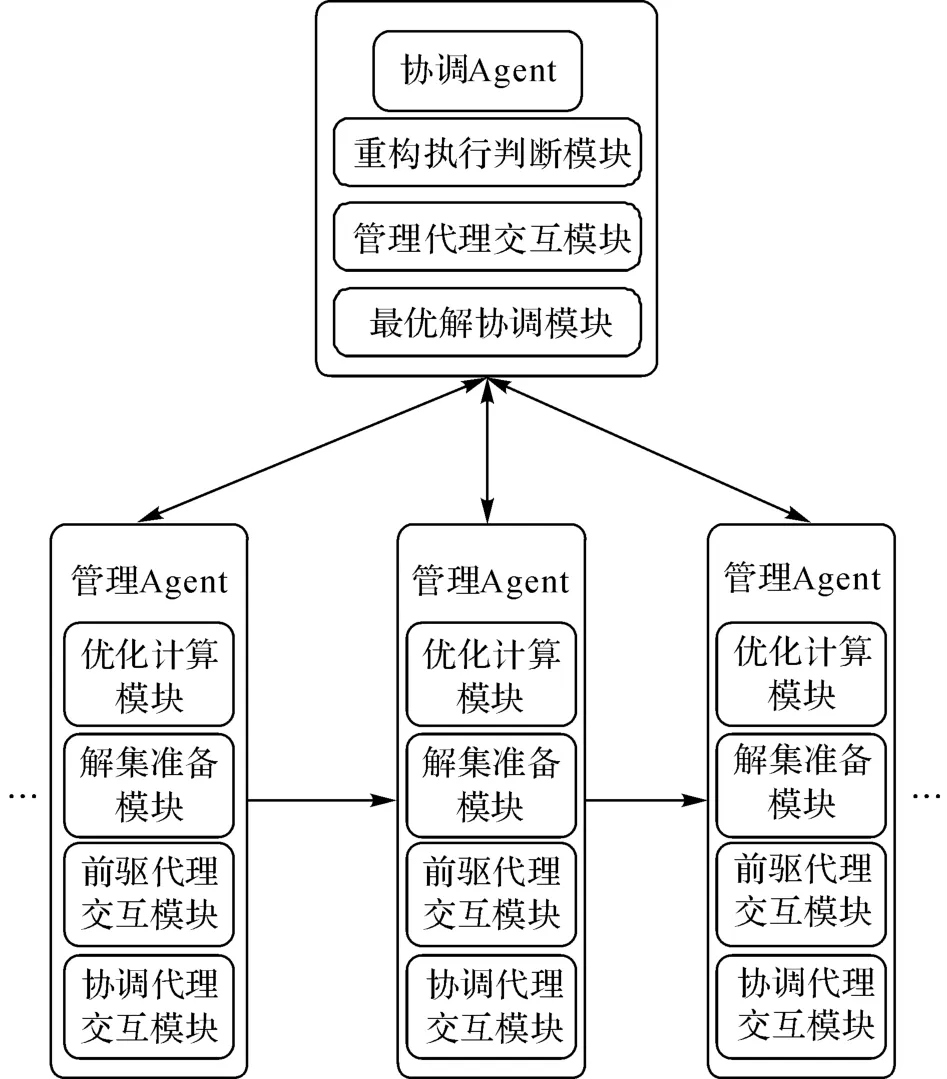
圖2 多智能體系統架構Fig.2 Multi-agent system architecture

2）可靠性.目標函數的表達式為

式中：W為配電網所有閉合的開關集合，i、j分別表示開關兩端節點；Kirjisk為支路ij的故障率，這樣每條支路均獲得一個表征可靠性的權重，每條閉合支路的計算結果由2部分組成，分別為專家經驗Eij

[19]和由下式表征的支路不可用率[20]：

其中，f為支路年故障頻率，r為故障平均恢復時間.

3）負荷分布均衡性.目標函數為

式中：Bi、Bsys分別為支路和系統的負荷平衡指數，Si、分別為流過支路的功率和支路的容量，Nb為系統總支路數.

每次重構過程中需要滿足的約束條件如下.

1）支路容量約束為

式中：Sl和Slmax分別為第l條支路流過的功率及最大值.

2）節點電壓約束為

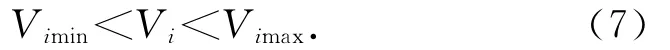
式中：Vi為節點電壓，Vimin、Vimax分別為節點電壓的最小和最大允許值.

3）無孤島約束：重構后拓撲結構呈輻射狀，不存在孤島.

4）潮流約束為

式中：Pi和Qi為節點i的輸入功率，PDGi和QDGi為節點i的DG注入功率，PLi和QLi為節點i的負荷功率，Nb為配電網的節點總數，Vi和Vj分別為節點i和節點j的電壓幅值，Gij為節點i和j間的電導，Bij為節點i和j間的電納，θij為節點i和j間的相位差.

3 改進粒子群算法

3.1 算法描述

提出改進的粒子群算法以及學習和競爭機制，每個管理Agent負責一個粒子Agent群體，粒子Agent的生存環境為一個環形網格，稱為智能體網格.網格規模為LSIZE×LSIZE，在智能體網格的空間中第i行第j列的智能體為Lij，智能體在網格中的位置由其行列號確定.

智能體粒子群引導的最短路算法的每個粒子Agent代表粒子群算法中的一個粒子，算法過程描述如下.首先，初始化每個粒子Agent的位置與速度，搜索空間為d維.其中第i個粒子的d維位置表達式為Xi=（xi，1，xi，2，…，xi，d），d維速度的表達式為Vi=（vi，1，vi，2，…，vi，d），每個粒子Agent的位置向量作為配電網所有邊的權值，即粒子位置的每一維對應閉合所有聯絡開關的電網結構中的一條邊，該維的值等于邊的權值，初始權值采用隨機初始化獲取.然后利用Dijkstra算法生成所有節點到電源點路徑最短的拓撲結構，計算每個粒子對應的3個目標函數f，通過下式分別求取每個粒子的Agent適應值：

每個粒子Agent可以與其鄰域內的粒子Agent進行競爭，設定粒子Agent Lij感知范圍為a，則能與Lij發生競爭作用的網格中的所有粒子Agent構成Lij的鄰域，鄰域中的所有粒子Agent為

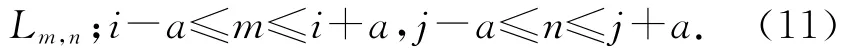
由于智能體網格為環形，采用下式對Agent的編號進行調整：

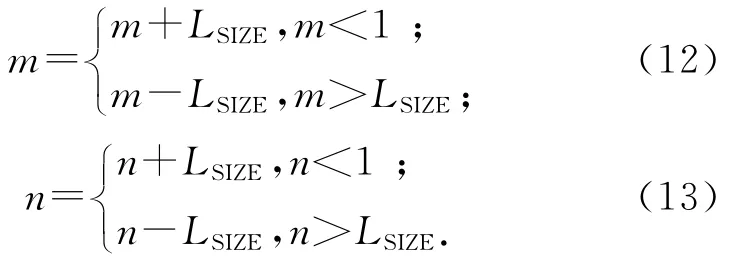
智能體的存活條件為3個目標函數中至少有一個滿足下式：

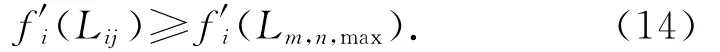
每個粒子Agent自身找到的最優解為Pi=（pi，1，pi，2，…，pi，d），整個種群找到的最優解為Pg=（pg，1，pg，2，…，pg，d），粒子群算法的修正公式為

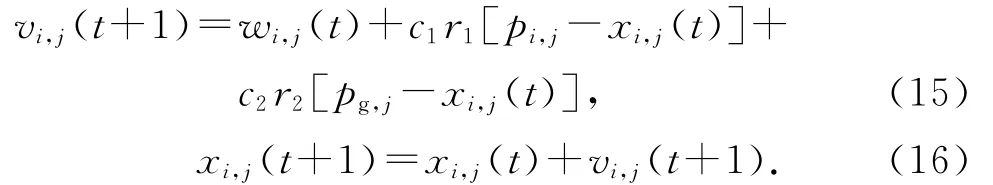
式中：w為慣性權重，c1和c2為正的學習因子，r1和r2為0～1.0的隨機數.

對基本粒子群算法的機制進行改進，每個智能體Lij均通過與其鄰域中的所有智能體比較適應值完成競爭操作.對于不能存活的智能體，采用粒子群算法的修正公式（15）和（16）修改速度和位置，將得到的新的智能體代替原來的智能體.通過智能體粒子群算法有方向地引導最短路徑的生成，可以使得到的拓撲結構逐漸向最優解逼近.

3.2 算法流程

當配電網達到觸發重構條件時，按照如下流程進行重構，算法流程如圖3所示.

4 層次分析法最優解決策

采取層次分析法確定最優解.主要步驟如下.

1）建立遞階層次結構.當應用AHP分析決策問題時，首先需要構造層次結構模型.這些層次可以分為以下3類.

a）最高層：只有一個代表優化目標的元素，本文中即為解的優先級順序.

圖3 重構算法流程圖Fig.3 Flow chart of reconfiguration solution

b）中間層：包含為實現目標所涉及的中間環節，包括所需考慮的準則和子準則，本文中即為3個目標函數代表的評價原則.

c）最底層：包括為實現目標可供選擇的各種措施、決策方案等，本文中即為解集中解的優先次序.

2）構造判斷矩陣并賦值.層次分析法重要性的標度含義如表1所示.

表1 層次分析法重要性標度含義表Tab.1 Intensity scale of importance for AHP method

以矩陣形式表示為判斷矩陣：

對于任何判斷矩陣，都滿足：

在構造判斷矩陣時，只需寫出上三角部分.

根據3個目標函數的重要性，構造準則層判斷矩陣如下：

3）層次單排序與檢驗.對每一列執行歸一化操作，得到的結果是一致性判斷矩陣權重.非一致性判斷矩陣是對列向量求算術平均值，即為權重：

CI越大，判斷矩陣的一致性越差；當CI=0時，判斷矩陣具有完全一致性.

為了檢驗判斷矩陣的一致性，需要計算它的一致性指標：

5 算例分析

5.1 重構判斷和最優解確定機制

本文的重構判斷條件為：基于匹配度的事件觸發機制.具體方法如下：以文獻[21]的光照數據作為數據來源，假設該城市內各光伏電源所接受的太陽光強密度相同，以對應的前五天的每小時的真實光伏電源輸出功率作為RBF神經網絡輸入數據，預測當前時刻下一小時的光伏電源輸出功率，光伏陣列輸出功率及額定功率的比值為匹配度，算例1和2中的負荷功率與匹配度成正比.頻繁重構容易對電網帶來過大的影響，所以匹配度不宜選得過小；選得過大，則會導致敏感度不足.本文設定距離上一次重構匹配度差值變化超過20％觸發一次新的重構，這樣在上一個整點即可完成下一個整點的重構，重構具有超前性.

將解集中優先次序最高的解作為初始最優解，剩余解按順序形成替補解集.若初始最優解不滿足開關動作次數約束，則按順序搜索替補解集，直至找到滿足開關次數約束的替補解作為當次重構最優解為止；或者替補解集中的所有解均不滿足開關次數約束，則放棄當次重構結果，配網結構保持與上次重構最優解一致，開關不動作.

5.2 算例1

美國PG＆amp；E69節點系統為12.66k V的配電網絡，包含74條支路和5個聯絡開關，有功負荷為3.802 MW，無功負荷為2.694 MVar.在該算例中，加入DG后的網絡結構及編號如圖4所示，DG1～DG4安裝光伏陣列，數量分別為3、3、2、1套，等效成PQ節點；DG5和DG6為容量分別為100和200k W的燃料電池，在燃料電池中，電力電子變換器功率調節單元輸出交流可控的有功出力和電壓幅值[22]，潮流計算時可以作為PV節點類型處理.取LSIZE為6，則智能體個數為36，取c1=c2=2，最大迭代次數為100，前、后兩次迭代過程中所有節點的最大電壓幅值修正量小于10-6k V為收斂條件.

根據重構觸發機制，可以判斷在該典型日的7、9、12、17、20時需要進行重構.在Windows 8.1 Enterprise操作系統、英特爾i7-4700MQ四核CPU2.40 GHz、8 GB內存配置下，仿真平臺采用Matlab8.4（R2014b），軟件自帶工具條統計的算法執行一次耗時163.230 s，其中潮流計算部分耗時75.442 s.仿真結果如圖5所示，其中開關組合狀態1、2、3、4分別記作S1、S2、S3、S4.

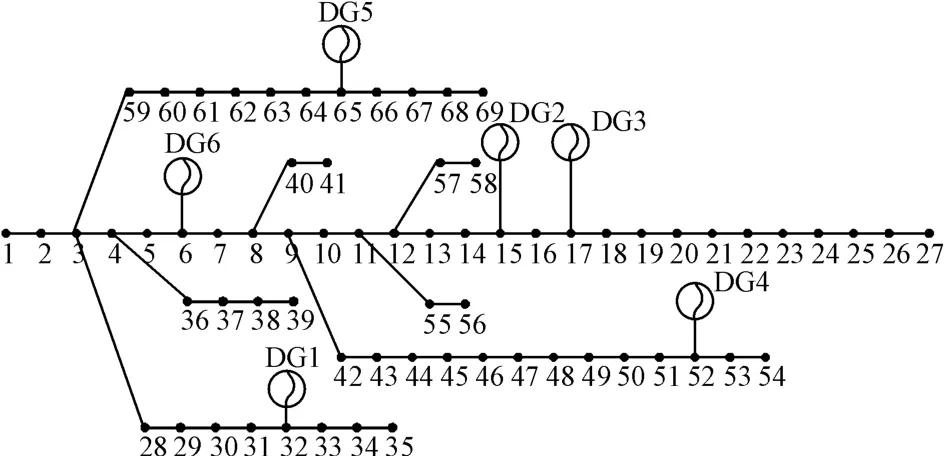
圖4 加入分布式電源后的69節點配電系統結構圖Fig.4 Sixty-nine-bus distribution system integrated with DGs

開關組合狀態1為模型初始狀態，即開關39～48、27～54、15～69、13～20、11～66斷開，其余均閉合.若一次開關都不允許動作，則5次重構均放棄最優解，開關組合狀態保持初始狀態，如圖5（a）所示.開關組合狀態2為39～48、27～54、15～69、13～20、59、60打開，開關組合狀態3為39～48、50、51、17、18、13～20、59、60打開；開關組合狀態4為39～48、50、51、14、15、13～20、59、60打開.從圖5（c）可以看出，當允許的開關變化次數足夠時，7時到12時的最優結構相同；圖5（b）顯示，當相鄰兩次開關變化限制為一對時，7時重構協調Agent放棄開關變化兩次的最優解，選擇狀態2開關變化一次的替補解.

圖5 各個時段的動態重構結果Fig.5 Results of each time interval after dynamic reconfiguration

圖5（a）～（c）對應的網絡損耗Loss如圖6所示的A方案、B方案和C方案.從圖6可以看出，配電網重構后的降損效果十分顯著.開關次數限制為一次和兩次以上只影響7：00～9：00的狀態，所以在開關操作較敏感的場合，可以將開關次數限制到一個較小的值.

對于可靠性指標，采用最大值和最小值差值歸一化的方式進行加權：

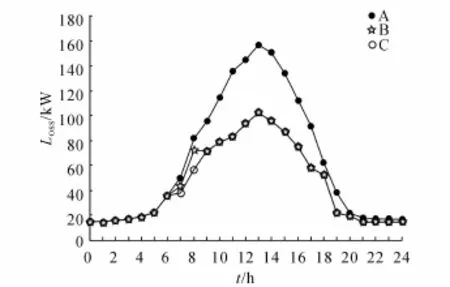
圖6 重構前、后的損耗對比Fig.6 Network loss before and after reconfiguration

圖5（a）～（c）對應的可靠性變化曲線如圖7所示的A～C方案.圖中，Krisk為不可靠性指標.

相比于初始結構，重構后的拓撲的可靠性增加，但是在7：00～9：00時間段內B方案不如C方案可靠.從圖6可知，該時間段內B方案的網損比C方案小；多目標優化最終的最優解并未使所有目標函數達到最優，部分目標函數是次優的；改變層次分析法對于目標重要性的評價等級，會改變重構結果，可以根據網損或者可靠性以及其他指標的不同側重來調整最優解決策的層次分析法評價體系.不同于網損與負荷變化有關，可靠性指標和拓撲結構對應，拓撲不變化，可靠性歸一化得到的值不會變，所以圖7的曲線只在重構時間點才有可能變動.

圖7 算例1重構前、后可靠性指標對比Fig.7 Unavailability of example1 before and after reconfiguration

5.3 算例2

在IEEE33節點測試系統上重新運行該算法，模型中有32條支路、5條聯絡開關支路、1個電源網絡首端基準電壓12.66k V、三相功率準值取10 MVA、系統有功負荷為5.084 MW，無功負荷為2.547 MVar.其他條件不變，DG1-DG6接入位置分別為5、12、16、20、23、30，DG1-DG4對應光伏陣列，數量分別為5、5、3、3套，等效成PQ節點；DG5和DG6為容量分別為200和300k W的燃料電池，等效成PV節點，其他條件同算例1，仿真耗時約為87.362 s.以7時為例，MATLAB作出最優電網結構，如圖8所示.

IEEE33節點測試系統的動態重構結果如表2所示.

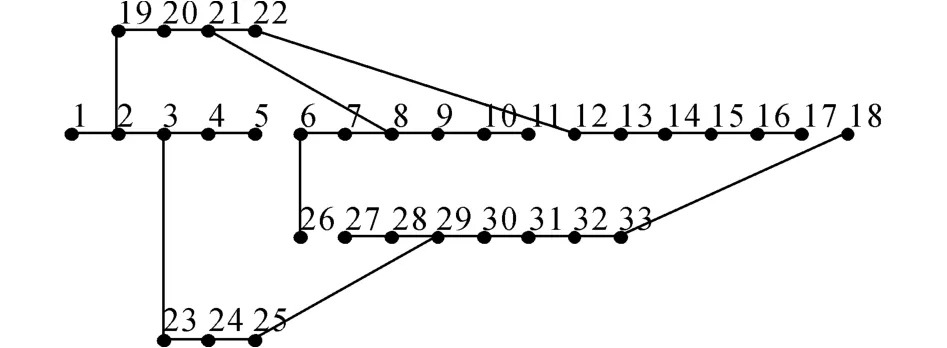
圖8 7：00重構的最優電網結構Fig.8 Optimal network structure of seven o’clock

表2 IEEE33節點算例動態重構結果Tab.2 Dynamic reconfiguration results of IEEE33 node distribution network

從表2可以看出，將開關次數限制值增加到2次以上之后的降損效果不明顯，所以可以將開關次數限制為2次以內，限制開關次數2次以內時損耗較大，所以一般情形下可以限制開關操作次數為2 次，從而在2個指標之間取得一個權衡.

從圖9可以看出，不同于算例1，在算例2中，對于允許開關次數分別為≥3和1兩種情況來說，前者不僅網損小，在后者放棄最優解采用替補解的9：00～20：00時間段，前者的不可靠性更小，即可靠性更高，優于后者.

圖9 算例2重構前、后可靠性指標對比Fig.9 Unavailability of example2 before and after reconfiguration

6 結 語

本文針對當前含有大量具有間歇性的分布式可再生電源接入的主動配電網，通過引入多智能體系統思想，提出基于多智能體協同尋優的主動配電網動態拓撲重構方法和算法設計.通過結合IEEE-33節點和美國PG＆amp；E 69節點2個典型算例，對所提出的方法進行仿真實驗驗證.結果表明，采用該方法能夠有效地計及分布式電源出力隨機性及其他不確定因素對配電網重構的影響，具有良好的計算效率和算法穩定性.本文提出的方法具有一定的普適性，對含有多種異質分布式發電滲透率不斷提高的主動配電網的自愈能力和負荷供電可靠性提升具有重要意義.

在本文的基礎上，未來工作將重點考慮配電網重構過程中對于網絡中重要負荷供電的支撐以及配電網絡在重構中可能采取的不同運行模式，例如分布式電源與負荷構成若干孤島運行系統，或分布式電源退出運行等模式.

（

）：

[1]LUAN W P，IRVING M R，DANIEL J S.Genetic algorithm for supply restoration and optimal load shedding in power system distribution networks[J].IEEE Proceedings of Generation，Transmission and Distribution，2002，149（2）：145-151.

[2]ZHU J Z.Optimal reconfiguration of electrical distribution network using the refined genetic algorithm[J].Electric Power System Research，2002，62（1）：37-42.

[3]余健明，蔡利敏，楊文宇.基于提高系統可靠性降低網損的配電網絡重構[J].電工技術學報，2004，19（10）：70-73.

YU Jian-ming，CAI Li-min，YANG Wen-yu.Distribution network reconfiguration for system reliability improvement and power loss reduction[J].Transactions of China Electrotechnical Society，2004，19（10）：70-73.

[4]李海鋒，張堯，錢國基，等.配電網故障恢復重構算法研究[J].電力系統自動化，2001，25（16）：34-37.

LI Hai-feng，ZHANG Yao，QIAN Guo-ji，et a1.Study on the algorithm for service restoration reconfigurati0n in distribution networks[J].Automation of Electric Power Systems，2001，25（16）：34-37.

[5]葛朝強，唐國慶，王磊.綜合智能式的故障恢復專家系統與故障恢復算法集相結合的自學習模糊專家系統[J].電力系統自動化，2000，24（2）：17-21.

GE Zhao-qiang，TANG Guo-qing，WANG Lei.Integrated intelligent service restoration system for distribution network：an auto-learning fuzzy expert system combined with service restoration algorithm set[J].Automation of Electric Power Systems，2000，24（2）：17-21.

[6]王淳，高元海.采用最優模糊C均值聚類和改進化學反應算法的配電網絡動態重構[J].中國電機工程學報，2014，34（10）：1682-1691.

WANG Chun，GAO Yuan-hai.Dynamic reconfiguration of distribution network based on optimal fuzzy C-means clustering and improved chemical reaction optimization[J].Proceedings of the CSEE，2014，34（10）：1682-1691.

[7]王成山，鄭海峰，謝瑩華，等.計及分布式發電的配電系統隨機潮流計算[J].電力系統自動化，2005，29（24）：39-44.

WAND Cheng-shan，ZHENG Hai-feng，XIE Ying-hua，et al.Probabilistic power flow containing distributed generation in distribution system[J].Automation of E-lectric Power Systems，2005，29（24）：39-44.

[8]李傳健，劉前進.考慮風力發電隨機性的配電網重構[J].電力系統自動化，2010，34（20）：34-39.

LI Chuan-jian，LIU Qian-jin.Distribution network reconfiguration considering randomness of wind power generation[J].Automation of Electric Power Systems，2010，34（20）：34-39.

[9]吳小珊，張步涵，袁小明，等.求解含風電場的電力系統機組組合問題的改進量子離散粒子群優化方法[J].中國電機工程學報，2013，33（4）：45-52.

WU Xiao-shan，ZHANG Bu-han，YUAN Xiao-ming，et al.Solutions to unit commitment problems in power systems with wind farms using advanced quantum-inspired binary PSO[J].Proceedings of the CSEE，2013，33（4）：45-52.

[10]FULLER J F，FUCHS E F，ROESLER K J.Applying multi-agent system technology in practice：automated management and analysis of SCADA and digital fault recorder data[J].IEEE Transactions on Power Systems，2006，21（5）：559-567.

[11]段濤，陳維榮，戴朝華，等.多智能體搜尋者優化算法在電力系統無功優化中的應用[J].電力系統保護與控制，2009，37（14）：10-15.

DUAN Tao，CHEN Wei-rong，DAI Chao-hua，et al.Reactive power optimization in power system based on multi-agent seeker optimization algorithm[J].Power System Protection and Control，2009，37（14）：10-15.

[12]趙文清，張勝龍，牛東曉.多Agent在變壓器故障診斷中的研究[J].電力自動化設備，2011，31（1）：23-27.

ZHAO Wen-qing，ZHANG Sheng-long，NIU Dong-xiao.Transformer fault diagnosis based on multi-Agent [J].Electric Power Automation Equipment，2011，31（1）：23-27.

[13]孟安波，劉永前，傅闖.分布分層的水電廠預知維護多Agent系統[J].電力自動化設備，2010，30（11）：105-109.

MENG An-bo，LIU Yong-qian，FU Chuang.Hierarchical distributed multi-Agent system of hydropower plant predictive maintenance[J].Electric Power Automation Equipment，2010，30（11）：105-109.

[14]趙傳霖，吳文傳，張伯明.基于多Agent的能量管理系統支持平臺[J].電力系統自動化，2009，33（7）：47-52.ZHAO Chuan-lin，WU Wen-chuan，ZHANG Bo-ming.

Multi-Agent based software platform for new generation of EMS[J].Automation of Electric Power Systems，2009，33（7）：47-52.

[15]李傳健，劉前進.基于Multi-agent和粒子群引導最小生成樹的配電網重構算法[J].電力系統保護與控制，2011，39（6）：24-29.

LI Chuan-jian，LIU Qian-jin.A distribution network reconfiguration algorithm based on multi-agent system and minimum spanning tree led by particle swarm optimization[J].Power System Protection and Control，2011，39（6）：24-29.

[16]盧志剛，楊國良，張曉輝，等.改進二進制粒子群優化算法在配電網絡重構中的應用[J].電力系統保護與控制，2009，37（7）：30-34.

LU Zhi-gang，YANG Guo-liang，ZHANG Xiao-hui，et al.Reconfiguration of distribution network based on improved particle swarm optimization[J].Power System Protection and Control，2009，37（7）：30-34.

[17]李振坤，陳星鶯，余昆，等.配電網重構的混合粒子群算法[J].中國電機工程學報，2008，28（31）：35-41.

LI Zhen-kun，CHEN Xing-ying，YU Kun，et al.Hybrid particle swarm optimization for distribution network reconfiguration[J].Proceedings of the CSEE，2008，28（31）：35-41.

[18]汲國強，吳文傳，張伯明，等.以降損和載荷均衡為目標的地區電網網絡重構快速算法[J].電網技術，2012，36（11）：172-178.

JI Guo-qiang，WU Wen-chuan，ZHANG Bo-ming，et al.Regional network reconfiguration algorithm for loss reduction and loading equilibrium[J].Power System Technology，2012，36（11）：172-178.

[19]XIE C S，DONG D P.Safety evaluation of smart grid based on AHP-entropy method[J].Systems Engineering Procedia，2012，4：203-209.

[20]LI W Y，ZHOU J Q.Power system risk assessment using a hybrid method of fuzzy set and Monte Carlo simulation[J].IEEE Transactions on Power Systems，2008，23（2）：336-343.

[21]李承熹，楊強，顏文俊.含分布式光伏電源的微電網孤島動態運行策略[J].電力系統保護與控制，2013，41（8）：99-105.

LI Cheng-xi，YANG Qiang，YAN Wen-jun.Dynamic islanding operation of microgrid with distributed photovoltaic generators[J].Power System Protection and Control，2013，41（8）：99-105.

[22]代江，王韶，祝金鋒.含分布式電源的弱環配電網絡潮流計算[J].電力系統保護與控制，2013，39（10）：37-42.

DAI Jiang，WANG Shao，ZHU Jin-feng.Power flow method for weakly meshed distribution network with distributed generation[J].Power System Protection and Control，2013，39（10）：37-42.

MAS-based cooperative optimization of reconfiguration in active power distribution networks

DONG Ru-liang，YANG Qiang，YAN Wen-jun

（College of Electrical Engineering，Zhejiang University，Hangzhou 310027，China）

A multi-agent system（MAS）based optimization framework was presented and the particle swarm optimization（PSO）algorithm was incorporated to identify the optimal topology reconfiguration scheme in a cooperative manner for active distribution network with distributed generation（DG）.Compared with the existing solutions，the approach can significantly reduce the negative impact due to frequent reconfigurations based on event-driven mechanism，while promotes the power supply security and economical benefits.The proposed algorithm solution was evaluated by using the IEEE 33-bus and PG＆amp；E 69-bus networks as the test networks.The numerical results demonstrate the effectiveness of the suggested approach in finding the optimal topology reconfiguration solution with acceptable computational complexity and communication overhead.

distribution network；distributed generation；multi-agent；particle swarm；shortest path algorithm；analytic hierarchy process（AHP）

TM 732

A

1008-973X（2015）10-1982-08

2014-09-02.浙江大學學報（工學版）網址：www.journals.zju.edu.cn/eng

浙江省自然科學基金重點資助項目（Z15E070001）；浙江省公益性技術應用研究計劃資助項目（2013C31005）.

董如良（1990—），男，碩士生，從事配電網拓撲重構、電力系統規劃、分布式發電的研究.E-mail：Charles TungZJU@gmail.com

楊強，男，副教授，博導.ORCID：0000-0002-0660-1312.E-mail：qyang@zju.edu.cn