基于氣動肌肉仿人下肢動力學

姜飛龍，陶國良，劉 昊，趙 勇，李慶偉

（浙江大學 流體動力與機電系統國家重點實驗室 浙江 杭州310027）

氣動肌肉作為一種新型的氣動執行元件，與氣動執行主要元件氣缸相比具有高的功率／質量比、位置控制僅僅受壓力單個因素影響，以及類似于人類肌肉的柔順性等優點，因此氣動肌肉在仿生機器人具有廣闊的應用前景.

類似于人的肌肉分為單關節肌和多關節肌.以氣動肌肉作為動力源的機器人也分為單關節和多關節氣動肌肉驅動、以及混合驅動的仿生機器人.其中，單關節氣動肌肉驅動仿生機器人主要包括：Kawamura等［1］設計的雙足步行機器人“Lucy”包括氣動、閥組、控制和通信單元，由對拉肌肉驅動2條腿共6個自由度.控制器主要包括軌跡控制器和剛度控制器，Δp 控制系統壓力，PI和Bang-Bang控制系統建模誤差實現軌跡控制.在線調整剛度控制器與主動動態軌跡控制結合，減小系統的能量消耗.把拉肌肉驅動的腿簡化為倒立擺機構，通過選擇不同的速度、步長，用零力矩點的方法實現步態腳踝變換.Shadow 公司［2］研制“Shadow Walker”每條 腿6個自由度，以木質為支架，安裝有張力傳感器、壓力傳感器、角度傳感器、高速開關閥、控制電路，對平衡和步態進行研究.Hosoda等［3-6］設計由對拉肌肉驅動的“Pneumat-BT 機器人”，并且控制直立行走；設計的氣動機器人集成CO2儲氣瓶、閥、電路板、電池為一體，通過調整閥的開關時間實現控制機器人的行走.設計的14根氣動肌肉驅動的氣動機器人，控制閥的通氣時間調整氣動肌肉的剛度，實現行走、跳躍、奔跑3種運動模式的切換.多關節或者單關節與多關節混合的氣動肌肉驅動仿生機器人主要包括：Hosoda等［7］兩關節和單關節肌肉共同驅動的下肢，分析跳躍時每根肌肉工作的時間和順序，以及運動中2種類型的肌肉分別起到協調和提供動力源的作用.Ogawa等［8］設計的全關節機器人共21個自由度腰關節、髖關節、踝關節分別為3 自由度球關節、2自由度萬向節，其他關節為具有1個自由度的鉸鏈，以陀螺儀和加速度傳感器為反饋信號控制完成站立和行走的動作.Niiyama 等［9-10］設計的全關節機器人共21個自由度以陀螺儀和加速度傳感器為反饋信號控制其完成站立和行走的動作，設計的兩關節和單關節肌肉共同驅動下肢，分析全方位力輸出，同時還研究模仿人的跑步機器人.

上述的仿生機器人大多局限在平面的氣動肌肉對拉形式的仿生機器人，沒有考慮到人在下肢運動包括矢狀面和冠狀面2個人體平面的運動，因此經過對人體下肢結構分析，本文設計了基于氣動肌肉的仿人下肢，對所設計的機械結構簡化為柔性并聯機構，求解仿人下肢的結構矩陣，有利于進一步了解各下肢肌的運動和力輸出特性.通過單剛體形式的氣動肌肉、虛功原理、結構矩陣相結合推導了包含肌肉的仿人下肢髖關節動力學方程，同時仿真分析了各肌肉的運動學特性.

1 下肢結構分析

下肢肌由盆帶肌、大腿肌和小腿肌組成，由肌肉產生動力支撐人體的體重、行走和維持直立姿態.

1.1 人體下肢肌

盆帶肌主要是起于骨盆、止于股骨上部的肌肉群，主要作用是通過神經系統驅動大腿屈、伸、外展、內旋［11］，按照肌肉所處的位置和作用可以分為前群（內側群）和后群（外側群）；前群包括：髂肌、腰大肌和闊筋膜張肌；后群包括：淺層的臀大肌、中層的臀大肌、臀中肌、梨狀肌、閉孔內肌、股方肌、深層的臀小肌、閉孔外肌；前群和后群使髖關節前屈和旋外、后伸和外旋.

大腿肌按照肌肉所處的位置和作用可以分為前外側群、內側群和后群，其中后群起于坐骨，跨過髖關節和膝關節，止于脛骨、腓骨的肌肉群；前外側群主要是股四頭肌，其中包括股直肌、股中間肌、股外側肌、股內側肌；內側群包括深層的短收肌、大收肌和淺層的恥骨肌、長收肌、股薄肌；后群包括半腱肌、半膜肌、股二頭肌；前外側群、內側群、后群的主要作用是髖關節和膝關節伸屈、髖關節內收、髖關節伸和膝關節屈.

小腿肌按照肌肉所處的位置和作用可以分為前群、后群和外側群，其中前群、后群分別位于骨間膜的前面、后面，外側群位于腓骨外側面；前群包括拇長伸肌、趾長伸肌和脛骨前肌；后群包括淺層的比目魚肌、腓腸肌和深層的脛骨后肌、趾長屈肌、拇長屈肌、腘肌；外側群包括腓骨長肌、腓骨短肌；前群、后群、外側群的主要作用是小腿和足趾伸、足跖屈、足外翻和踝關節屈.小腿缺少驅動其進行旋轉運動的肌肉，旋轉運動的實現主要依靠大腿肌肉驅動.

1.2 人體下肢骨

骨與骨之間用纖維組織、軟骨或骨結合形成骨連接，按照連接的方式可以分為直接連接和間接連接.直接連接由纖維組織或軟骨直接連接，基本不活動，又可以進一步分為纖維、軟骨、骨連接.間接連接又稱關節，為含有滑液的腔隙僅借助周圍的結締組織囊相連接，分為關節面、關節囊、關節腔，具有較大的活動性.關節的運動分為兩關節面相對滑動引起的移動、沿冠狀軸的屈伸、沿矢狀軸的收展、沿垂直軸的旋轉和上端固定下端做圓周運動的環轉.

按照關節的運動軸的數量和關節面的形狀，關節可以分為單軸（只有一個運動軸）、雙軸（有2個互相垂直的運動軸）和多軸關節（有3個互相垂直的運動軸）.單軸關節又可以分為屈戊關節（股骨和脛骨、腓骨連接的關節）和車軸關節（脛骨與腓骨之間連接的關節）；雙軸關節又可以分為橢圓關節（脛骨與跗骨連接的關節）和鞍狀關節；多軸關節又可以分為球窩關節（股骨與髖骨連接的關節）和平面關節.

人的下肢自由度分配如下：髖關節具有屈伸、內收外展和內旋外旋3個方向的自由度，因此髖關節可以簡化為球鉸的形式；膝關節具有屈伸方向的一個自由度；踝關節具有與髖關節相同的屈伸、內收外展和內旋外旋3個方向的自由度，與此同時脛骨與腓骨之間具有相對轉動，把踝關節簡化為球鉸的連接形式，到實際情況在進行機械結構設計時，踝關節的內旋外旋運動轉移到膝關節，因此膝關節分別具有屈伸和內旋外旋、踝關節具有屈伸和內收外展2個自由度；各腳趾具有由一對氣動肌肉驅動的屈伸一個自由度.

1.3 仿人下肢結構設計

通過上述對人體下肢運動分析，如圖1所示得到人體下肢髖關節、膝關節、踝關節分別有3、2、2個自由度，用氣動肌肉和鋼絲繩配合取代人體肌肉，設計的仿生下肢如圖2所示，骨盆固定在支架上，股骨的兩端分別與骨盆、髖關節氣動肌肉固定板相連，股骨與骨盆之間采用桿端關節軸承連接以實現髖關節的旋轉運動.臀大肌、內收肌（恥骨肌、長收肌、短收肌）、髂腰肌、閉孔內肌、梨狀肌兩端分別與骨盆、驅動髖關節氣動肌肉固定板相連；其中臀大肌、內收肌（恥骨肌、長收肌、短收肌）、髂腰肌、閉孔內肌和梨狀肌驅動髖關節繞矢狀軸、冠狀軸、垂直軸旋轉.

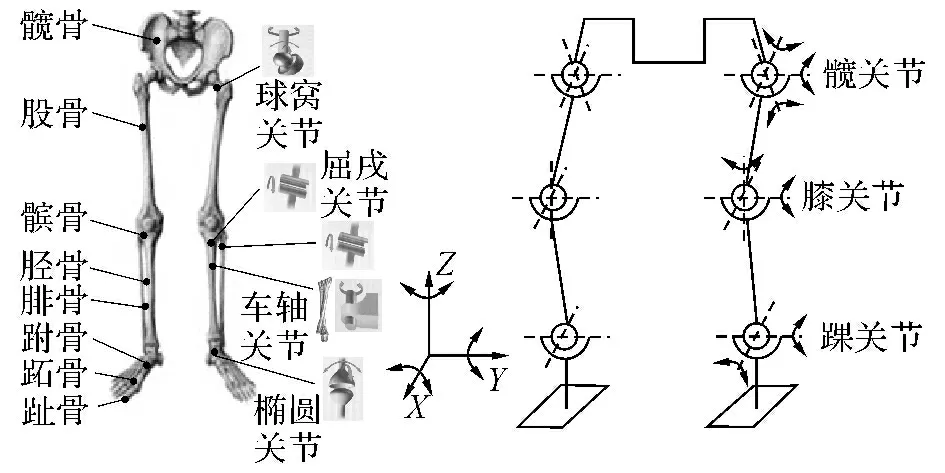
圖1 人體下肢關節自由度分布圖Fig.1 Human lower limb joint DOF distribution

驅動膝關節氣動肌肉固定板通過螺紋和桿端關節軸承兩端分別與股骨、腓骨相連，股直肌、大腿后側肌群（主要包括半腱肌和半膜肌）、股薄肌、股二頭肌兩端分別與骨盆、驅動膝關節氣動肌肉固定板相連；股直肌和大腿后側肌群（主要包括半腱肌和半膜肌）、股薄肌和股二頭肌驅動膝關節繞冠狀軸、垂直軸旋轉.

小腿三頭肌、前群肌（脛骨前肌、拇長伸肌、趾長伸肌）、外側群肌（腓骨長肌、腓骨短肌）兩端分別與驅動膝關節氣動肌肉固定板、腳相連接，小腿三頭肌、前群肌（脛骨前肌、拇長伸肌、趾長伸肌）、外側群肌在圓周上不同半徑夾角為120°均勻的分布在驅動膝關節氣動肌肉固定板上，實現驅動踝關節繞矢狀軸和冠狀軸旋轉.拇長屈肌、拇長伸肌、趾長屈肌、趾長伸肌固定在膝關節氣動肌肉固定板上，其中拇長屈肌和拇長伸肌驅動大腳趾屈伸，趾長屈肌和趾長伸肌驅動小腳趾屈伸.

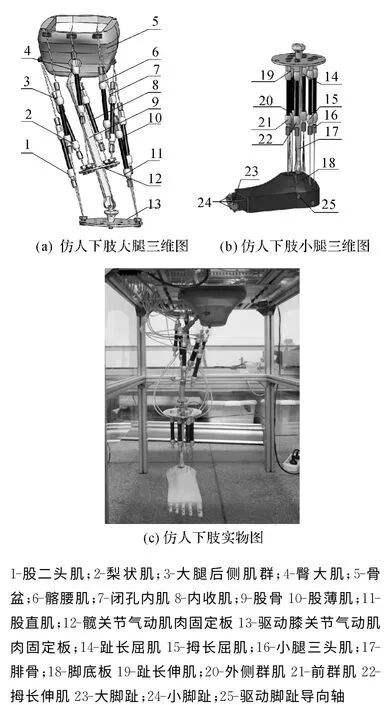
圖2 仿人下肢機械結構Fig.2 Humanoid lower limb mechanical structure

2 柔性并聯系統

為簡化起見，對設計的仿人下肢進行以下假設：1）不考慮氣動肌肉、股骨、腓骨等零件的質量；2）忽略關節處摩擦力和系統自身受到的重力；3）連接各固定點的氣動肌肉與鋼絲繩處于張緊狀態.

圖3 仿人下肢機構原理圖Fig.3 Humanoid lower limb mechanism principle diagram

基于氣動肌肉仿人下肢結構模型進行機構簡化如圖3所示，對簡化后的機構坐標定義如下：骨盆與固定支架接觸面的中心部分點為固定坐標原點O，其相應的坐標系定義為OXOYOZ，其X、Y、Z3個坐標軸分別平行并且在人體的矢狀面、水平面、冠狀面內，并且定義骨盆上固定鋼絲繩的不銹鋼夾頭的各點為A1、A2、A3、A4、A5、A6，定義髖關節處股骨與骨盆連接的桿端關節軸承運動球頭中心點為A0，參考坐標系為AXAYAZ，桿端關節軸承轉動處的連體坐標系為A′XA′YA′Z，初始位置的X 軸平行于人體冠狀軸取向前為正、Y 軸在冠狀面內并且向內為正方向、Z 軸滿足右手規則即同時垂直于X、Y 軸取向上為正，髖關節連體坐標系A′XA′YA′Z相對于參考坐標系AXAYAZ在X、Y、Z3個方向旋轉的角度分別為α1、β1、γ1.定義股骨與驅動膝關節運動的氣動肌肉固定平面相交中心點為B，參考坐標系為BXBYBZ，其中X、Y、Z3個坐標軸分別平行于人體的矢狀軸、冠狀軸、垂直軸，并且取向前、向內、向上為正，其上4處氣動肌肉固定點B1、B2、B3、B4.

同樣定義膝關節、踝關節處參考坐標系和連體坐標系，膝關節連體坐標系C′XC′YC′Z相對于參考坐標系CXCYCZ在Y、Z2個方向旋轉的角度分別為β2、γ2.踝關節連體坐標系D′XD′YD′Z相對于參考坐標系DXDYDZ在X、Y2個方向旋轉的角度分別為α3、β3.

3 運動學計算

3.1 關節位置反解

髖關節固定點A0處連體坐標系A′XA′YA′Z相對于參考坐標系AXAYAZ的坐標變換矩陣為

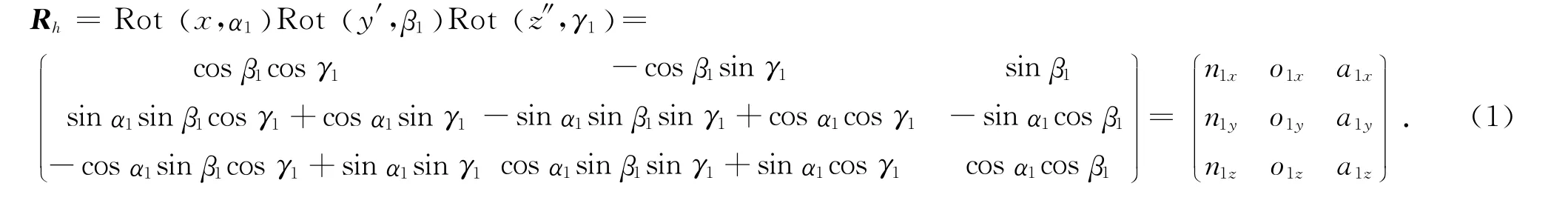
式中：x 為坐標系AXAYAZ的X 軸，y′、z″為坐標變換過程中坐標軸y、z 一次性轉換、二次轉換，n1x、o1x、a1x、n1y、o1y、a1y、n1z、o1z、a1z表示坐標變換矩陣的各個量.

如圖4所示為大腿關節肌肉固定點坐標，骨盆各固定氣動肌肉點A1、A2、A3、A4、A5、A6在坐標系AXAYAZ中的坐標為

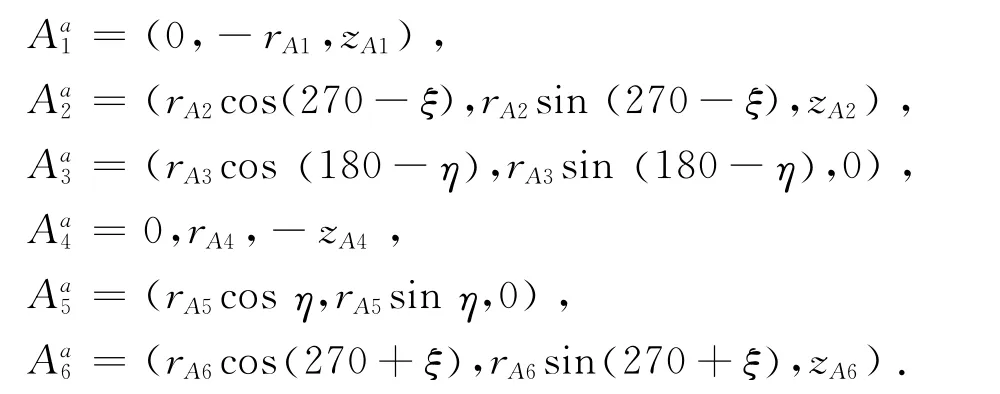
式中：rA1、rA2、rA3、rA4、rA5、rA6分 別 為A1、A2、A3、A4、A5、A6以 圓 柱 坐 標 系 表 示 時 各 圓 的 半 徑；zA1、zA2、zA3、zA4、zA5、zA6為各點相對于坐標AXAYAZ在垂直方向的坐標；ξ、η 為A2、A2、A3相對于坐標AXAYAZ的方向角.

設定B1、B2、B3、B4各點相對于坐標系BX、BY、BZ的轉角為φ，則各點在坐標系中的坐標為

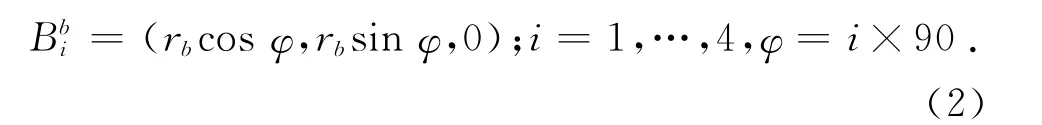
同時B0在坐標系AXAYAZ中的坐標Ph為

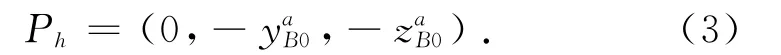
因 此 可 以 表 示B1、B2、B3、B4各 點 在 坐 標 系AXAYAZ中的坐標Bai為

髖關節各氣動肌肉連接點之間的距離ln為

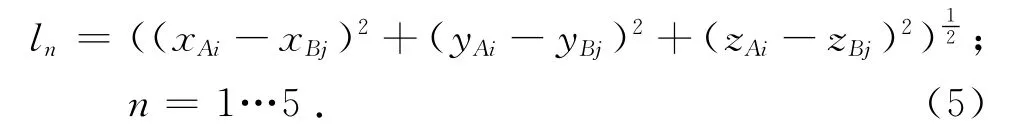
式中：xAi、yAi、zAi為骨盆處肌肉坐標，xBj、yBj、zBj為股骨處肌肉坐標.

膝關節、踝關節用類似的方法計算，如圖5所示為小腿關節肌肉固定點坐標.其中膝關節固定點C0處連 體 坐 標 系C′XC′YC′Z相 對 于 參 考 坐 標 系CXCYCZ的坐標變換矩陣為

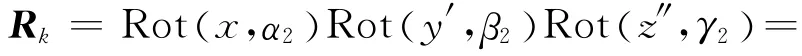
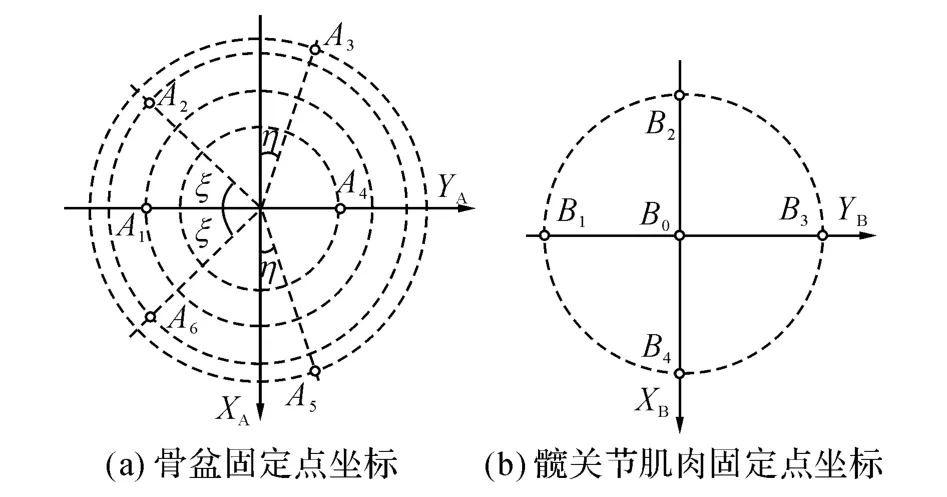
圖4 大腿關節肌肉固定點坐標Fig.4 Muscle fixed point coordinate of thigh joint

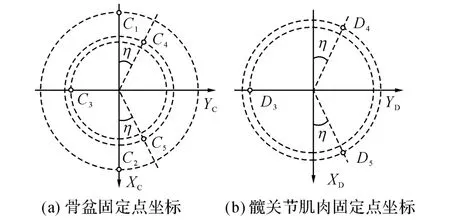
圖5 小腿關節固定點坐標Fig.5 Muscle fixed point coordinate of ankle joint

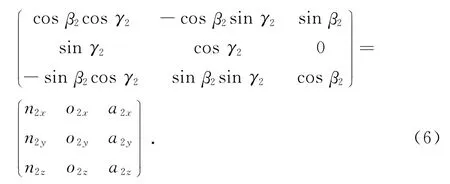
式中：n2x、o2x、a2x、n2y、o2y、a2y、n2z、o2z、a2z表示坐標變換矩陣的各個量.

連體坐標系C′XC′YC′Z相對于參考坐標系AXAYAZ的坐標變換矩陣為

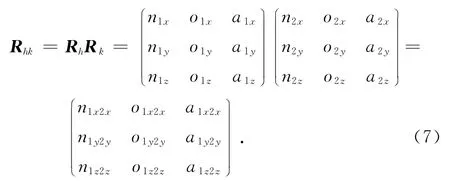
式中：n1x2x、o1x2x、n1y2y、o1y2y、a1y2y、n1z2z、o1z2z、a1z2z為坐標轉換的各量.

3.2 關節雅可比矩陣

髖關節空間的姿態可以由θb＝ ［α1，β1，γ1］T中的各個分量表示，因此驅動髖關節髖關節運動的肌肉為

對式（5）關于時間求導得

因此

式中：Jh為髖關節驅動肌肉分布的結構矩陣.

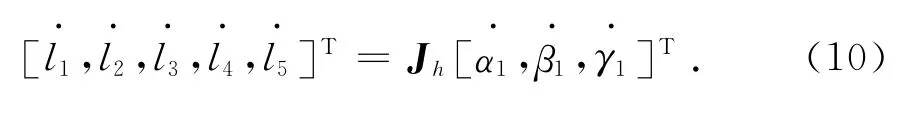
4 動力學建模

根據力學平衡方法，并聯機構的動力學計算方法主 要 有：拉 格 朗 日［13-16］、虛 功 原 理［17-19］、牛 頓-歐拉［20-22］等方法，每種方法各有其優劣.拉格朗日方法計算比較復雜；虛功原理把系統作為一個整體，不需要計算系統內力，計算動力學簡單方便，關鍵是虛位移、虛速度、虛角速度的轉換，此方法適應于本論文中髖關節質心的分布難以確定特點；牛頓-歐拉方法計算清晰，但是需要考慮內力，適應于膝關節結構簡單對稱、質心容易確定的特點.

坐標系BXBYBZ相對坐標系AXAYAZ坐標變換Rn為

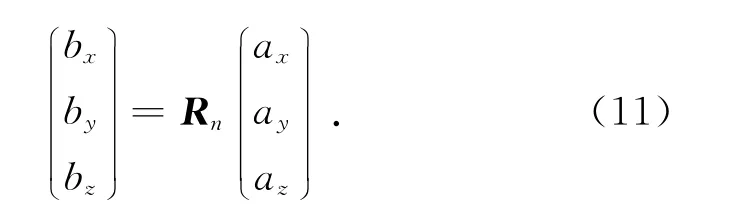
則存在如下關系

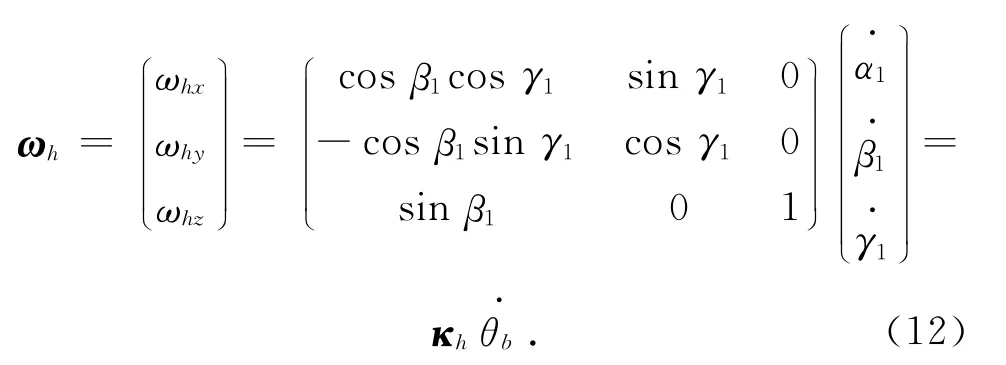
式中：ωh為角速度，ωhx、ωhy、ωhz分別為角速度在x、y、z3個方向的分量，κh為髖關節驅動肌肉固定坐標到骨盆對應固定肌肉點的轉換矩陣.

4.1 位置分析

以氣缸和液壓缸作為驅動元件的并聯機構系統，氣缸和液壓缸簡化為由活塞桿和缸筒構成的多剛體系統［19-20］，需要同時考慮2部分的虛速度、虛角速度運動特性.在本系統中鋼絲繩的質量與氣動肌肉的質量相比較可以忽略不計，氣動肌肉的分析受力可以簡化為如圖6所示為髖關節氣動肌肉坐標示意圖的變質心單剛體系統.設在股骨的廣義獨立坐標為＝［vh，ωh］T，其中，vh為線速度，考慮到由氣動肌肉驅動的股骨僅可以繞X、Y、Z3個坐標軸的旋轉，因此髖關節的廣義獨立坐標可以表示為＝［0，ωh］T.由式（9）得髖關節驅動肌肉的輸入輸出特性為

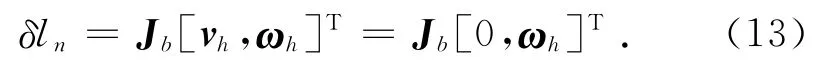
式中：δ為對氣功肌肉位移的求導；Jb為廣義坐標系的變換矩陣.

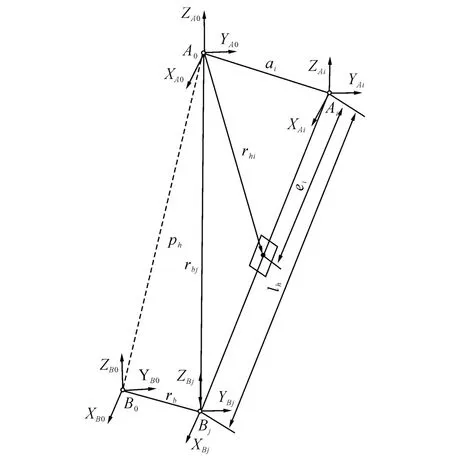
圖6 髖關節氣動肌肉坐標示意圖Fig.6 Schematic diagram of PAM in hip joint

由式（8）和（13）得

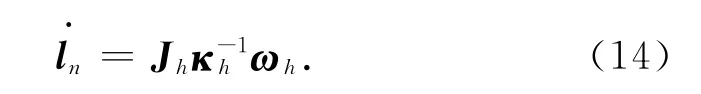
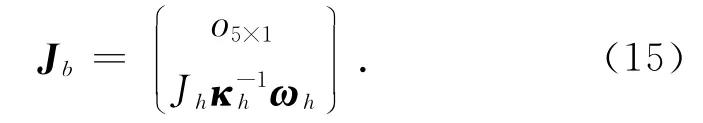
由圖6驅動髖關節的氣動肌肉閉環為

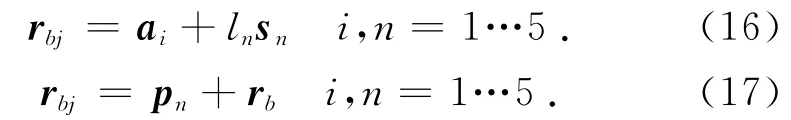
式中：rbj為股骨旋轉點到驅動髖關節肌肉在股骨固定點的相對位置，sn為氣動肌肉的單位矢量，ai為氣動肌肉在骨盆的坐標相對坐標系AXAYAZ的位置，相對位置，pn為坐標BXBYBZ與坐標AXAYAZ的相對位置.

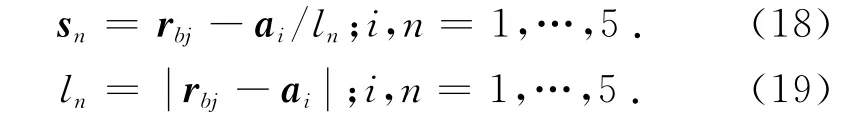
Ai點的初始坐標系為AixAiyAiz在股骨運動后Ai點的坐標系轉換為A′ixA′iyA′iz，其變換矩陣為［20］

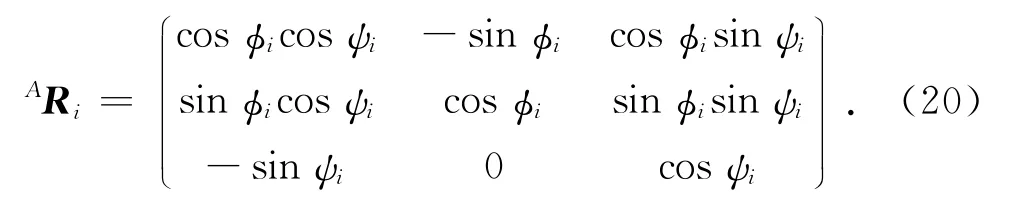
式中：φi 和ψi 為坐標轉換過程中分別繞Aiz軸和A′iy軸的旋轉角度.

由上式有下列關系可知氣動肌肉的單位矢量sn為

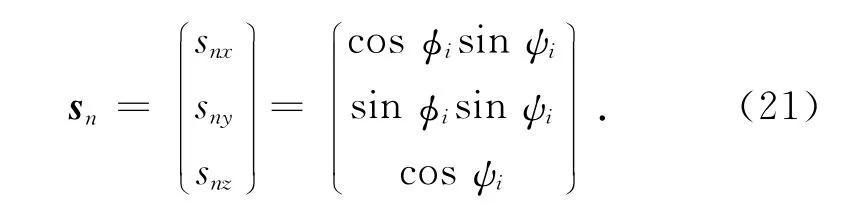
氣動肌肉的質心為

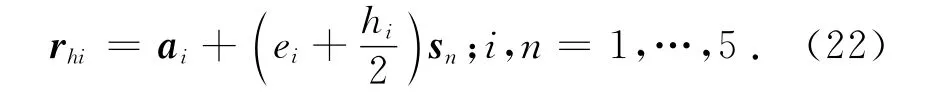
式中：ei為為氣動肌肉骨盆固定點到氣動肌肉橡膠管中心的距離，hi為氣動肌肉收縮長度.

4.2 速度分析

對式（16）關于時間求導得

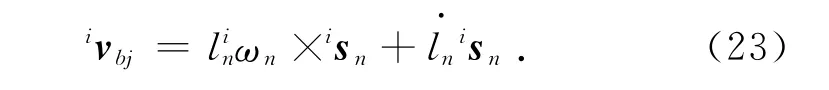
用isn點乘上式得

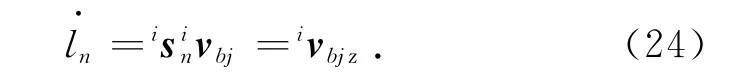
用isn叉乘式（23），可以得到氣動肌肉的轉動角速度為

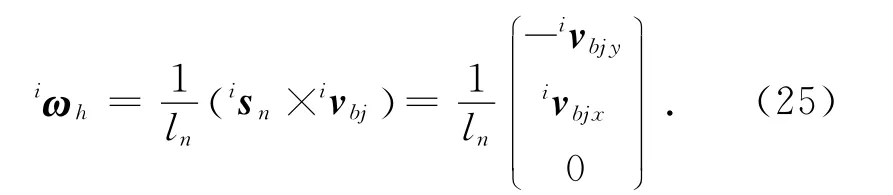
對式（23）關于時間求導得到氣動肌肉收縮速度為

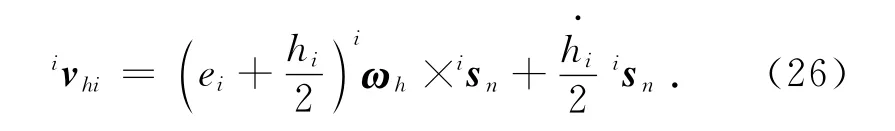
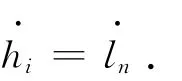
所以

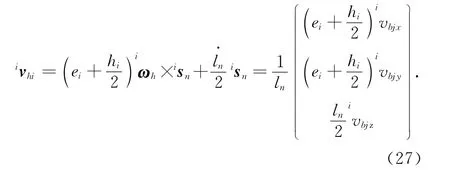
對式（17）關于時間求導得速度計算公式

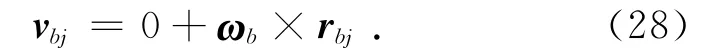
上式寫成矩陣形式為

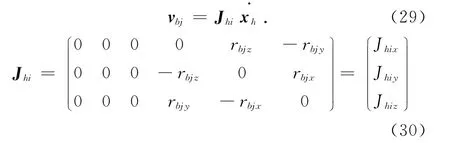
式中：rbjx，rbjy，rbjz為rbj在x，y，z三個方向的分量，Jhi為氣動肌肉的線速度在廣義坐標系表示的系數，Jhix，Jhiy，Jhiz為Jhi的元素，由式（20）和（29）聯立得到氣動肌肉坐標系表示的速度

其中iRA＝.

聯立式（29）和（31）得到

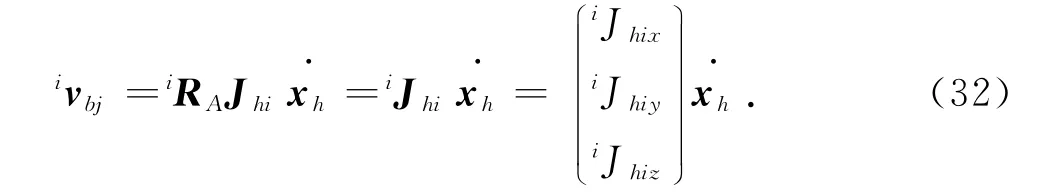
式中：iJhix、iJhiy、iJhiz為系數矩陣在氣勁肌肉坐標系X、Y、Z3個方向的分量.

聯立式（25）、（29）、（32）得氣動肌肉的線速度ivhi和角速度iωh在廣義坐標系表示為

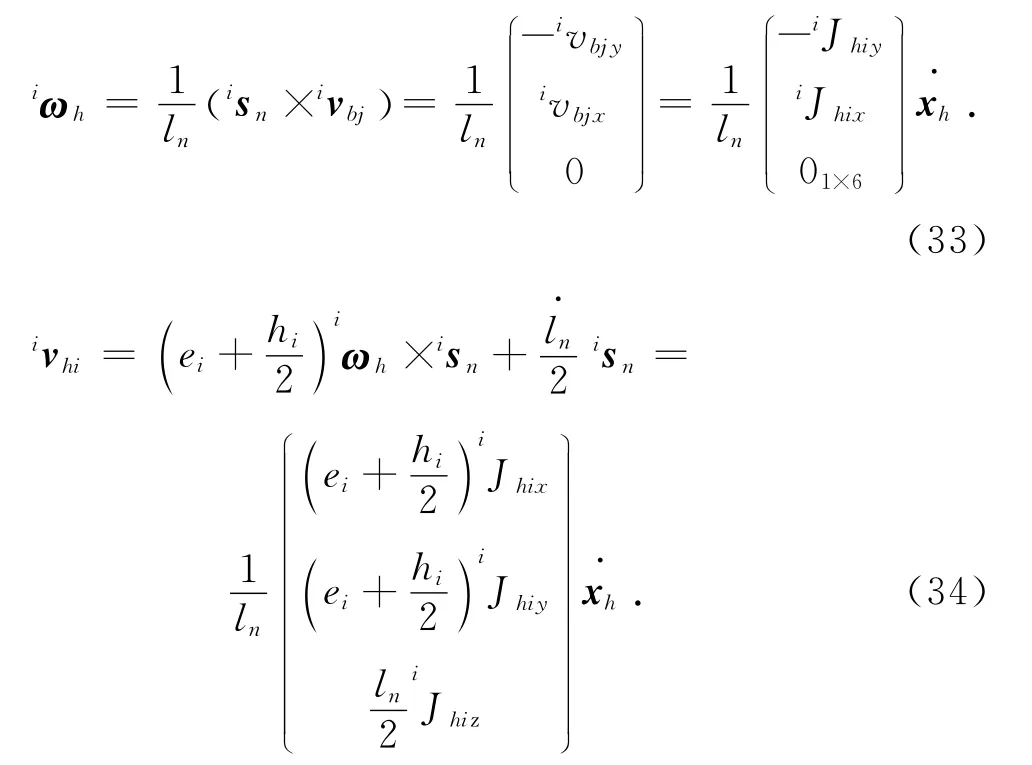
即

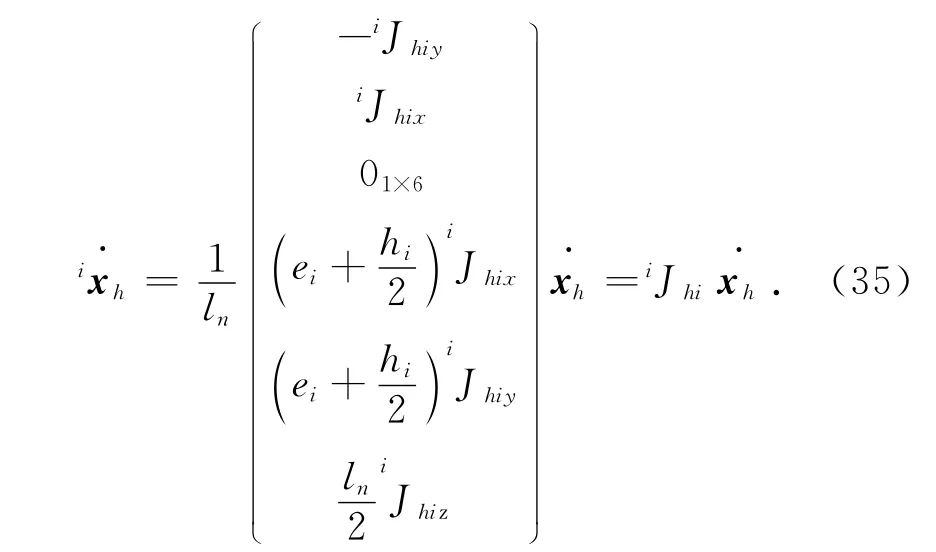
4.3 加速度分析

對式（28）關于時間求導得加速度計算公式：

轉換到氣動肌肉坐標系的加速度為

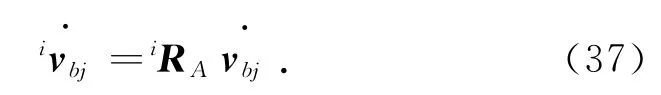
對式（23）關于時間求導得加速度計算公式：

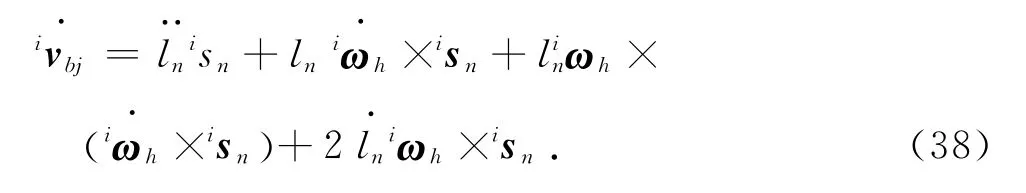
用isn點乘式（38）得

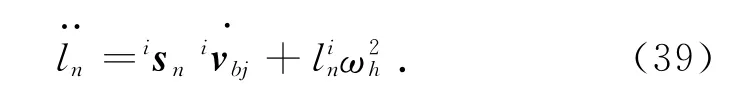
用isn叉乘式（38）得

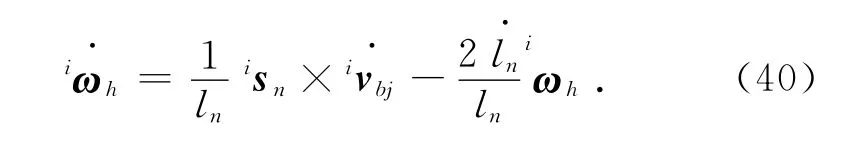
氣動肌肉收縮加速度的計算公式為

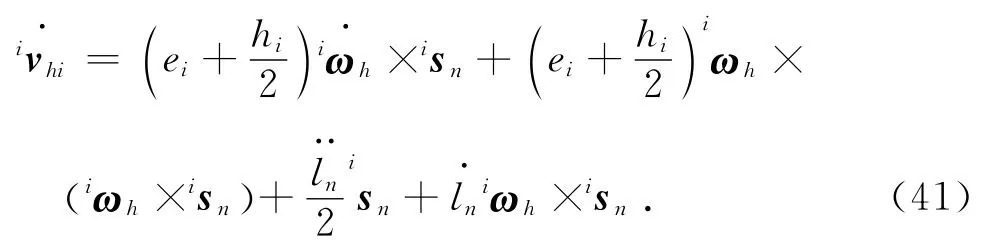
4.4 外力和慣性力

仿人下肢髖關節受到的外力和慣性力可以分為股骨和各驅動髖關節氣動肌肉分別受到的外力和慣性力.

1）股骨受力分析

對于股骨，作用在質心的外力和慣性力為

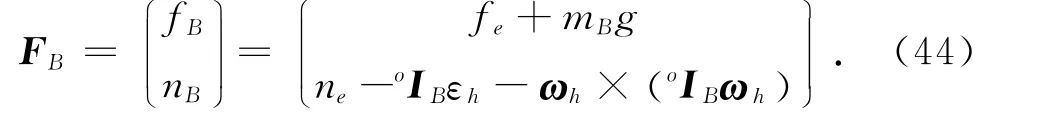
式中：fB、nB分別為作用在股骨質心處的外力、力矩之和，fe、ne分別為股骨受到膝關節、骨盆的作用力和股骨質心處所受到的力矩，mB為股骨的質量，g為重力加速度，oIB＝RhIBRTh為局部坐標系股骨的轉動慣量IB轉換到固定坐標系AXAYAZ的量，εh為髖關節在X、Y、Z3個方向的角加速度.

2）氣動肌肉受力分析

假設氣動肌肉所受到的外力僅僅為重力，則作用在各氣動肌肉的外力和慣性力可表示為

式中：fhi、nhi分別為作用在驅動髖關節運動各氣動肌肉質心處的外力和力矩，mhi為氣動肌肉的質量，iIhi為氣動肌肉在局部坐標系的轉動慣量矩陣.

4.5 動力學方程

根據虛功原理：髖關節處氣動肌肉的驅動力，股骨所受的外力、慣性力，氣動肌肉所受的外力、慣性力作用之和為零，得到髖關節動力學方程為

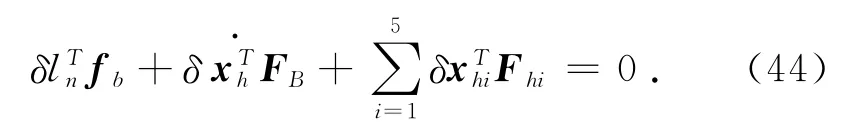
式中：fb＝［f1，f2，f3，f4，f5，］T為髖關節各氣動肌肉驅動力構成矢量.

聯立式（15）、（30）、（42）、（43）和（44）可得

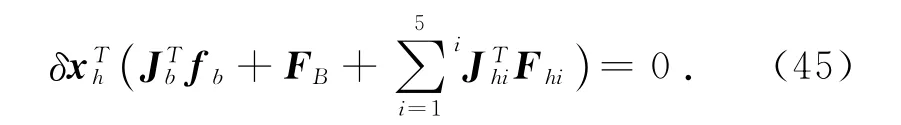
式（45）可進一步簡化為

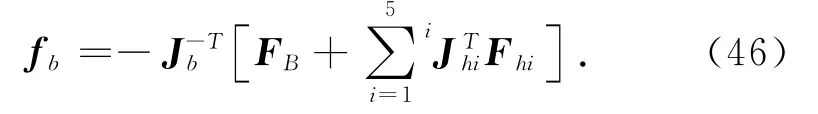
5 仿真分析

試驗測量人下肢運動各關節的角度，考慮到氣動肌肉收縮量相對較小，保持運動的頻率不變，減小各關節運動角度的幅值，各關節的轉角函數取（49）.

如圖7～9所示分別為髖關節、膝關節和踝關節肌肉位移特性，圖中L 為氣動肌肉的長度，δ 為步態周期.

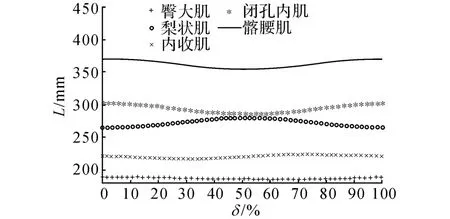
圖7 髖關節肌肉位移特性Fig.7 Hip joint muscle displacement characteristics

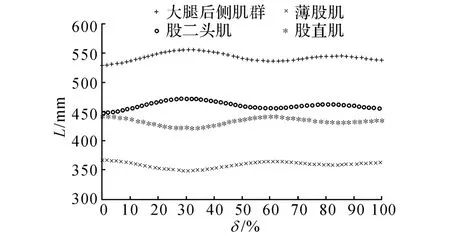
圖8 膝關節肌肉位移特性Fig.8 Knee joint muscle displacement characteristics

從圖7～9中可看出，在人下肢單腿運動周期內各肌肉運動如下：承重期到支撐相早期過渡：髂腰肌、閉孔內肌處于不收縮狀態，之后逐漸開始收縮直至支撐相中期結束收縮最大；梨狀肌處于收縮最大值，之后逐漸伸長直到支撐相末期；股直肌、薄股肌、小腿三頭肌、外側群肌基本不收縮，之后逐漸開始收縮直至支撐相中期中間位置，大腿后側肌群、股二頭肌則正好相反；小腿三頭肌、前群肌收縮量最大，逐漸伸長直至支撐相中期中間位置.

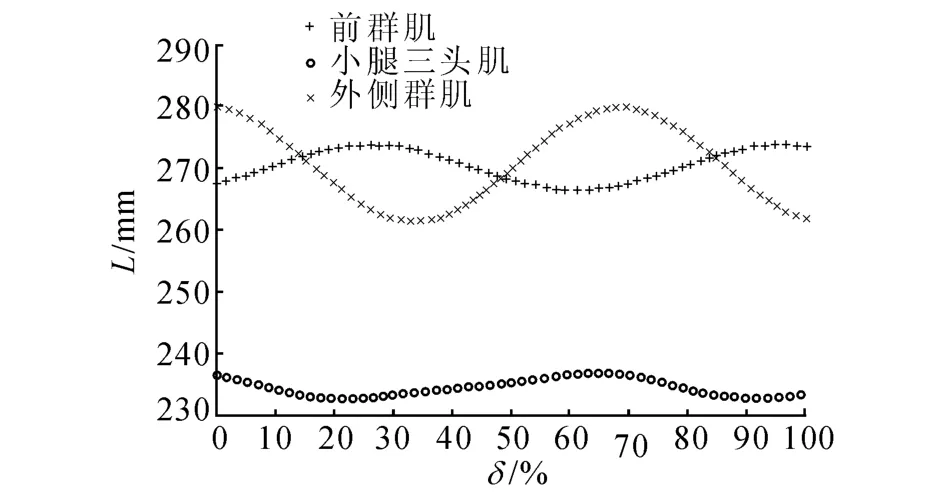
圖9 踝關節肌肉位移特性Fig.9 Ankle joint muscle displacement characteristics

支撐相中期：髂腰肌、閉孔內肌逐漸收縮，梨狀肌逐漸伸長；股直肌、薄股肌、小腿三頭肌、外側群肌逐漸收縮，在支撐相中期中間位置其收縮量到最大值，然后逐漸減小直到支撐相末期完全伸長；大腿后側肌群、股二頭肌、前群肌的運動情況正好相反.

支撐相中期：髂腰肌、閉孔內肌逐漸收縮，梨狀肌逐漸伸長；股直肌、薄股肌、小腿三頭肌、外側群肌逐漸收縮，在支撐相中期中間位置其收縮量到最大值，然后逐漸減小直到支撐相末期完全伸長；大腿后側肌群、股二頭肌、前群肌的運動情況正好相反.

支撐相中期至支撐相末期過渡：髂腰肌、閉孔內肌收縮量達到最大值，之后逐漸伸長，在擺動相末期完全伸長；梨狀肌完全伸長，之后逐漸收縮，到擺動相末期完全收縮.

支撐相末期到擺動相早期過渡：大腿后側肌群、股二頭肌、前群肌、小腿三頭肌收縮到極值，之后逐漸伸長擺動相中期；前群肌伸縮到最大，之后逐漸伸長直至擺動相末期；股直肌、股薄肌基本不收縮.

擺動相早期：股直肌、薄股肌、外側群肌逐漸伸長，并且外側群肌伸長到最大，然后逐漸收縮，直至擺動相末期.

擺動相中期：大腿后側肌群、股直肌逐漸伸長至最大值，然后開始收縮至擺動相末期；股二頭肌、股薄肌逐漸收縮至最大值，之后逐漸伸長，直至擺動相末期.

擺動相末期過渡：梨狀肌、閉孔內肌、大腿后側肌群、股二頭肌、小腿三頭肌、外側群肌收縮到一個極值；髂腰肌、閉孔內肌、股直肌、股薄肌、前群肌伸長到一個極值.

在單腿整個運動周期內，臀大肌、內收肌基本保持不動.

6 結 論

（1）對人下肢運動的驅動肌肉進行分析和關節運動副進行分類，設計了髖關節、膝關節、踝關節、腳趾分別具有3、2、2、5個自由度的仿人下肢，踝關節水平面內的旋轉運動移動到膝關節，膝關節具有矢狀面和水平面2個平面內的2個自由度，較形象的模擬人的下肢肌肉和關節運動副分布.

（2）以計算和仿真的方法求解解設計的仿人下肢單關節和多關節肌肉的運動學特性，基于虛功原理求解了氣動肌肉并聯機構的動力學，對于機器人、外骨骼、人體醫學的研究具有較大的參考價值.

（

）：

［1］VANDERBORGHT B，VANHAM R，VERRELST B，et al.Overview of Lucy project：dynamic stabilization of a biped powered by pneumatic artificial muscles［J］.Advanced Robotics，2008，22（10）：1027-1051.

［2］WALKER R.The shadow biped［EB／OL］.［2013-08-21］.http：∥www.shadow.org.uk／projects／biped.shtml

［3］TAKUMA T，HOSODA K.Controlling the walking period of a pneumatic muscle walker［J］.The International Journal of Robotics Research，2006，25（9）：861-866.

［4］HOSODA K，TAKUMA T，NAKAMOTO A，et al.Biped robot design powered by antagonistic pneumatic actuators for multi-modal locomotion［J］.Robotics and Autonomous Systems，2008，56（1）：46-53.

［6］NARIOKA K，HOSODA K.Design synergistic walking of a whole-body humanoid driven by pneumatic artificial muscles：an empiricial study ［J］.Advanced Robotics，2008，22（10）：1107-1123.

［7］HOSDA K，SAKAGUCHI Y，TAKAYAMA H，et al.Pneumatic-driven jumping robot with anthropomorphic muscular skeleton structure［J］.Auton Robot，2010，28（3）：307-316.

［8］OGAWA K，NARIOKA K，HOSODA K.Development of whole-body humanoid‘Pneumat-BS′with Pneumatic musculoskeletal system［C］∥Proceedings of 2011IEEE／RSJ International Conference on Robots and Systems Intelligent Robots and Systems（IROS）.［S.l.］：IEEE，2011：4838-4843.

［9］NIIYAMA R.Design principle based on maximum output force profile for a musculoskeletal robot［J］.Industrial Robot：an International Journal，2010，37 （3）：250-255.

［10］NIIYAMA R，NISHIKAWA S，KUNIYOSHI Y.Athlete robot with applied human muscle activation patterns for bipedal running［C］∥Proceedings of 2010 IEEE-RAS International Conference on Humanoid Robots.［S.l.］：IEEE，2010：498-503.

［11］柏樹令，應大君，丁文龍等.系統解剖學［M］.北京：人民衛生出版社，2010.

［12］黃真，趙永生，趙鐵石.高等空間機構學［M］.北京：高等教育出版社，2012：169-182.

［13］LIU Shan-zeng，YU Yue-qing，ZHU Zhen-cai，et al.Dynamic modeling and analysis of 3-RRS parallel manipulator with flexible links ［J］.Journal of Central South University，2010，17（2）：323-331.

［14］ABDELLATIF H，HEIMANN B.Computational efficient inverse dynamics of 6-DOF fully parallel manipulators by using the Lagrangian formalism ［J］.Mechanism and Machine Theory，2009，44（1）：192-207.

［15］YEN Ping-lang，LAI Chi-chung.Dynamic modeling and control of a 3-DOF Cartesian parallel manipulator［J］.Mechatronics，2009，19（3）：390-398.

［16］GUO H B，LI H R.Dynamic analysis and simulation of a six degree of freedom Stewart platform manipulator［J］.Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2006，220（1）：61-72.

［17］HUANG L，XU W L，TORRANCE J.Design of a position and force control scheme for 6RSS parallel robots and its application in chewing robots［J］.International Journal of Humanoid Robotics，2010，7（3）：477-489.

［18］DUAN Q J，DUAN X C.Analysis of cable-actuated parallel robot with variable length and velocity cable［J］.Procedia Engineering，2011（15）：2732-2737.

［19］TSAI LW.Solving the inverse dynamics of a Stewart-Gough manipulator by the principle of virtual work［J］.Journal of Mechanical design，2000，122（1）：1-9.

［20］李永剛，宋軼民，馮志友，等.基于牛頓-歐拉法的3-RPS并聯機構逆動力學分析.航空學報［J］.2007，28（5）：1210-1214.LI Yong-gang，SONG Yin-min，Feng Zhi-you，et al.Inverse dynamic of 3-RPS parallel mechanism by Newton-Euler formulation［J］.Acta Aeronautica Et Astronautica Sinica，2007，28（5）：1210-1214.

［21］WANG Jin-song，WU Jun，WANG Li-ping，et al.Simplified strategy of the dynamic model of a 6-UPS parallel kinematic machine for real-time control［J］.Mechanism and Machine Theory，2007，42 （9）：1119-1140.

［22］LEE SH，SONG JB，CHOI WC，et al.Position control of a Stewart platform using inverse dynamics control with approximate dynamics ［J］.Mechatronics，2003，13（6）：605-619.