基于擾動觀測器的多旋翼無人機機載云臺模糊自適應跟蹤控制

王日俊，白 越，續志軍，宮 勛，張 欣，3，田彥濤

（1.中國科學院長春光學精密機械與物理研究所，吉林長春130033；2.中國科學院大學，北京100039；3.長春工程學院電氣與信息工程學院，吉林長春130012；4.吉林大學通信學院，吉林長春130025）

基于擾動觀測器的多旋翼無人機機載云臺模糊自適應跟蹤控制

王日俊1，2，白 越1，續志軍1，宮 勛1，張 欣1，2，3，田彥濤4

（1.中國科學院長春光學精密機械與物理研究所，吉林長春130033；2.中國科學院大學，北京100039；3.長春工程學院電氣與信息工程學院，吉林長春130012；4.吉林大學通信學院，吉林長春130025）

為了補償多旋翼無人機機載云臺的擾動，實現機載云臺的穩定跟蹤控制，提出基于改進擾動觀測器的模糊自適應跟蹤控制方法.在原有擾動觀測器結構的反饋回路中引入一個補償控制，構建基于速度信號的改進型擾動觀測器結構，分析該結構的補償擾動能力和魯棒性；利用模糊系統的逼近性質和李雅普諾夫穩定性原理，設計相應的模糊自適應跟蹤控制結構，證明了該控制結構的穩定性.飛行實驗表明，應用該控制方法后，視軸穩定誤差的均方值小于0.02°，跟蹤給定位置信號的跟蹤誤差小于0.08°，完全能夠滿足多旋翼無人機機載云臺的穩定跟蹤控制.引入補償控制后的擾動觀測器補償擾動能力明顯提高，提出的控制方法具有較高的穩定跟蹤精度.

多旋翼無人機；機載云臺；擾動觀測器；跟蹤控制；模糊自適應；穩定性

多旋翼無人機（multi-motor unmanned aerial vehicle，m UAV）由于機動性強、起降靈活等特點被廣泛應用在偵察、目標捕獲、識別和跟蹤等領域.多旋翼無人機重量輕、體積小，所搭載的機載云臺極易受到姿態變化、機體振動、氣流擾動、摩擦以及其他未知擾動等因素的干擾，造成機載視頻圖像模糊、離焦甚至目標從視場中消失[1-2].一方面，容易造成操作人員視覺疲勞引發誤操作，甚至無法識別目標信息.另一方面，會導致偵察、跟蹤等任務無法完成.對多旋翼無人機機載云臺的擾動補償和穩定跟蹤控制的研究和方法改進有著重大的實際意義.

在目前的擾動補償方法中，Umeno等[3]提出的擾動觀測器（disturbance observer DOB）具有較強的擾動補償能力、運算量小、無需外部傳感器等特點，在機載穩定云臺的擾動補償上得到了廣泛的應用[4-6].李嘉全等[6]在控制系統中引入了一種擾動觀測器結構，對擾動進行估計和補償，改善了機載穩定平臺抑制擾動的能力，但是該結構難以對系統中存在的噪聲干擾進行補償.謝巍等[7]通過新增2個控制器設計一種改進的擾動觀測器，并在直流電機系統中驗證了抗噪聲干擾的魯棒性能.多旋翼無人機的自身特點決定了機載云臺擾動的非線性和強藕合性的特點，因此僅采用擾動觀測器結構來對機載云臺擾動進行補償控制，難以取得理想的穩定跟蹤效果.模糊系統和神經網絡等智能控制策略，因其魯棒性、實時性好、不依賴系統模型、具有逼近任何函數的性質等優點，已廣泛應用于穩定平臺的伺服跟蹤控制系統中.高篙等[8]針對機載光電跟蹤系統構造了基于模糊推理的變論域模糊控制器，保證了系統的性能要求，具有很好的實時性和魯棒性.朱海榮等[9]利用神經元的自學習和自適應能力，提出基于擾動補償的單神經元自適應PI控制策略，保證了穩定平臺在外界擾動和系統變化時平臺的穩定跟蹤能力.

本文針對多旋翼無人機機載云臺的擾動補償和穩定跟蹤控制要求，提出基于改進擾動觀測器的模糊自適應跟蹤控制方法.在現有擾動觀測器結構的基礎上，在反饋回路中引入一個補償控制結構，提高補償擾動的能力.利用模糊系統來在線估計機載云臺的其他未知擾動，進一步提升機載云臺的穩定精度，保證系統的穩定跟蹤性能，實現對多旋翼無人機機載云臺的擾動補償和精確跟蹤控制.

1 機載云臺系統建模

1.1 機載云臺建模

假設機載云臺是剛體，且旋轉中心與云臺的質心重合.根據Lagrange-Euler方程[10]可知，忽略離心力和科氏力，云臺的非線性模型方程與單關節機構的模型方程一致.

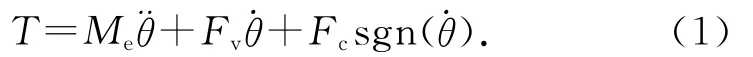
式中：Me為載荷的有效慣量，Fv為黏滯摩擦力（viscous friction），Fc為靜摩擦力（Coulomb friction）.將方程中的非線性項Fcsgn看作云臺的擾動項Tf，可得機載云臺的線性模型為

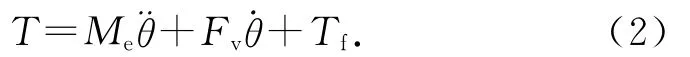
令x1=θ，x2=系統輸出y= x1，于是開環系統的空間狀態方程為

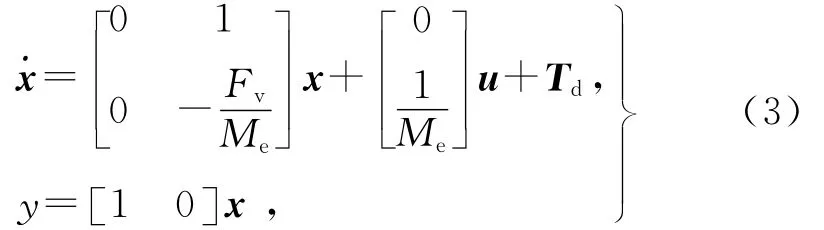
即

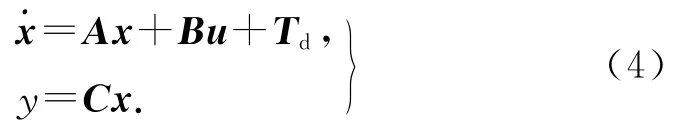
式中：

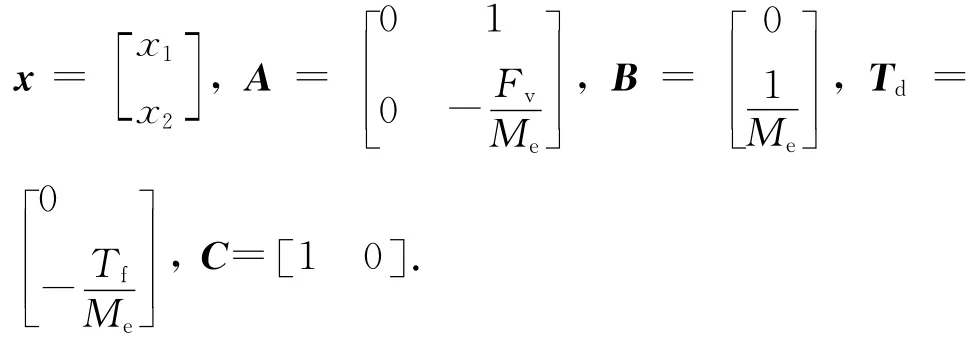
1.2 執行機構建模

該機載云臺采用直流電機作為執行機構，數學模型[11]為

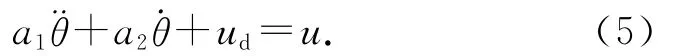
式中：θ為電機的位置角度，ud為擾動，u為控制輸出的電壓.在實際應用中，a1=+ δa2，其中和為變量a1和a2實際的測量值，δa1、δa2為擾動引起變量a1和a2發生的變化量.定義非線性未知擾動函數f（·）=+ud，f（·）包括模型誤差、參數波動、Td以及其他非線性未知擾動等，于是，

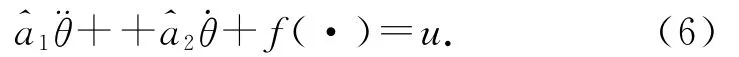
2 基于速度信號的改進型擾動觀測器設計

如圖1所示為由現有基于速度信號的擾動觀測器（velocity based disturbance observer，VDOB）構成的控制結構.

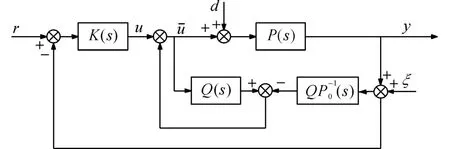
圖1 基于v DOB的控制系統結構Fig.1 VDOB-based control system structure

圖中，P（s）表示穩定平臺模型，P0（s）為平臺的標稱模型，信號r、d、ξ為系統的參考輸入、外界擾動以及噪聲干擾.實際上，d和ξ通常處于不同的頻率范圍，于是有如下假設.

假設1存在2個截止頻率ωl、ωh，且ωl＜ωh，噪聲干擾處于高頻范圍內ξ（jω）∈（ωh，∞），外界擾動及參考輸入均處于低頻范圍內，即d（jω）∈（0，ωl），r（jω）∈（0，ωl）.根據圖1，可得系統的傳遞函數為

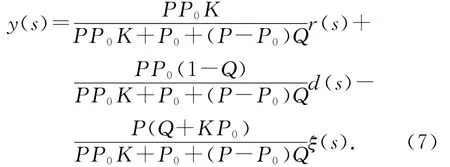
假設2如果在低頻范圍（0，ωl）內Q（s）≈1，在高頻范圍（ωh，∞）內Q（s）≈0.系統輸出可以近似地表示為

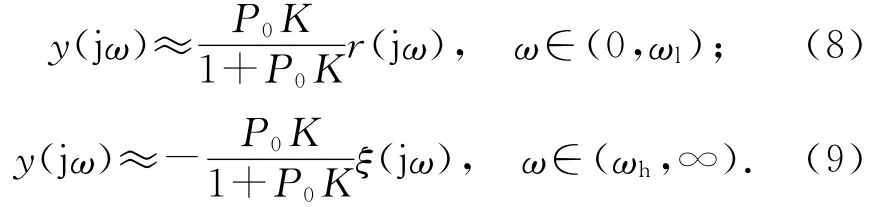
由此看出，基于VDOB的控制結構能夠完全消除外界擾動對系統輸出的影響，但是對高頻噪聲干擾的抑制作用不理想.針對上述情形，提出基于速度信號的改進型擾動觀測器結構（improved velocity based disturbance observer，IVDOB），如圖2所示.與VDOB相比較，在系統輸出的反饋信號端增加一個補償控制器Q2（s）用來補償系統的高頻干擾，提高補償高頻噪聲干擾的能力.

根據圖2，可得IVDOB的傳遞函數：

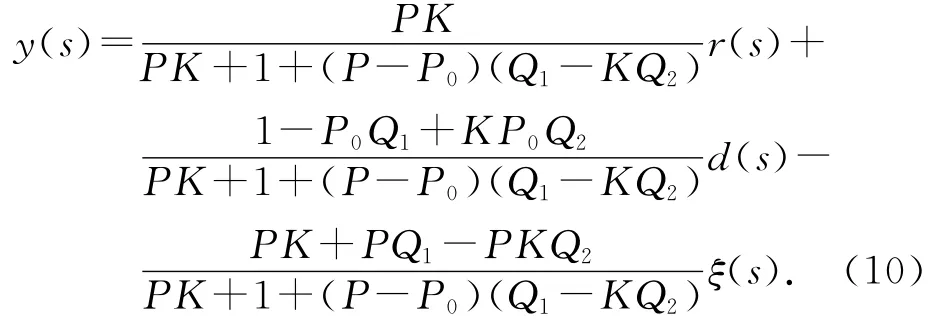
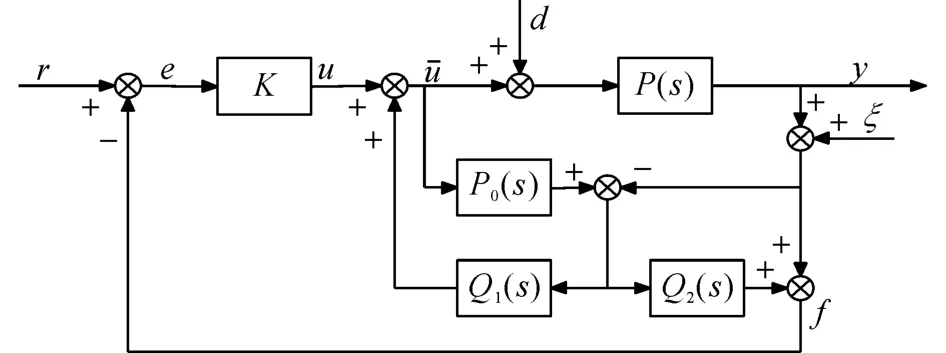
圖2 基于Iv DOB的控制系統結構Fig.2 IVDOB-based control system structure

為了既能補償外界擾動d，又能補償噪聲干擾ξ，Q1、Q2須滿足以下2個條件：

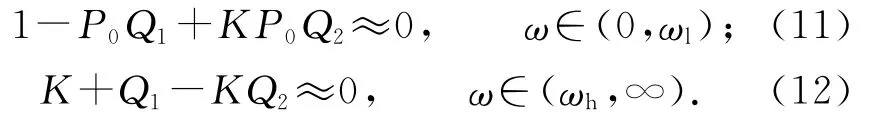
即

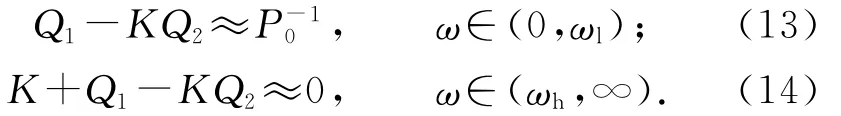
考慮如下情形.

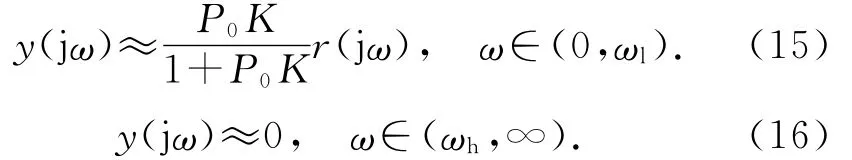
對于標稱模型的逆模型存在且穩定時，IVDOB不僅保證了對系統輸入很好的跟蹤性能，而且完全補償了系統的低頻擾動d.對比式（16）、（9）可知，ξ得到了很好的抑制.

若標稱模型P0（s）存在誤差，且模型誤差的集合可以用加法攝動來表示，即P0（s）=P（s）+W1Δ，其中W1為穩定有界的加權函數，P（s）、Δ（s）為嚴格有理穩定的函數.由魯棒穩定性定理可知，IVDOB魯棒穩定的充要條件為

定理1如圖2所示，假設P0（s）∈H∞，控制器K（s）滿足P0（s）對于閉環傳遞函數的穩定性要求，且滿足Q1P0+Q2=1時，則參考輸入r到控制器K（s）輸出u之間的閉環傳遞函數始終不變.即：Gur（s）=（1+KP0）-1K.

證明：圖2中，當d和ξ均存在時，可以得到如下關系式：

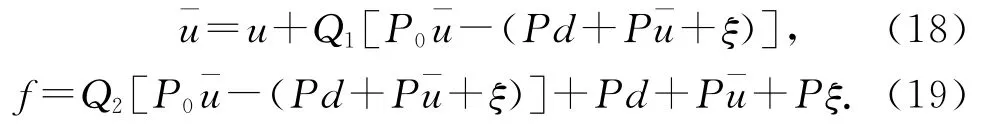
根據式（18）、（19），有

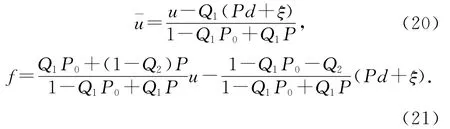
又因為Q1P0+Q2=1，代入式（21）有f=P0u，故Gur（s）=（1+KP0）-1K.定理得證.

3 模糊自適應控制器設計

采用基于IVDOB的控制結構，能夠對系統擾動進行補償，實現對機載云臺的視軸穩定控制.擾動觀測器的控制方法無法完全補償系統中存在的擾動，Miller等[12]指出，多旋翼無人機體積小、重量輕，且飛行環境惡劣，在飛行作業過程中存在很多非線性未知干擾，而這些擾動的存在使得機載云臺的穩定精度和跟蹤性能受到影響.鑒于上述分析，本文利用模糊系統的萬能逼近特性來進一步對系統的干擾進行補償[13]，設計機載云臺的模糊自適應控制器，提高了機載云臺的穩定精度和跟蹤性能.

基于IVDOB的模糊自適應控制結構如圖3所示.該控制結構采用雙閉環控制結構，其中速度環由IVDOB來控制實現，位置環由PD控制器、前饋控制器、模糊控制器以及魯棒控制器4部分組成.

模糊規則定義如下.R（j）：ifθ1isandθ2is，then ufis Bj，其中模糊系統的輸入=（θ1，θ2）=（θ，∈U，模糊系統輸出uf∈R是集合Ui（i=1，2）上的模糊集，Bj（j=1，2，…，N）是集合R上的模糊集.模糊系統根據上述規則，實現了從模糊集U∈R2到R的映射.依據模糊推理系統引理[14]，有

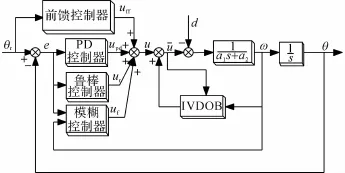
圖3 機載云臺控制系統原理圖Fig.3 Principle diagram of proposed control system structure for airborne platform

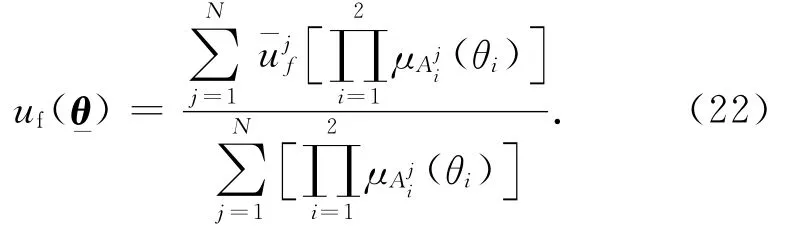
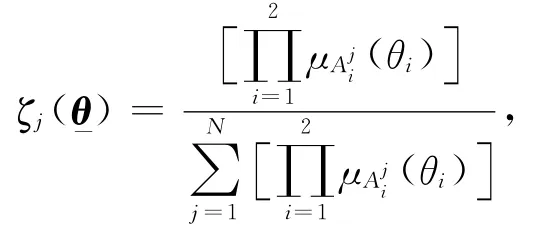
利用李雅普諾夫穩定理論來考察控制系統的穩定性.根據圖3得到系統的控制律為

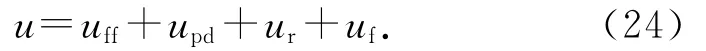
式中：uff=結合式（6），有

整理式（25），有

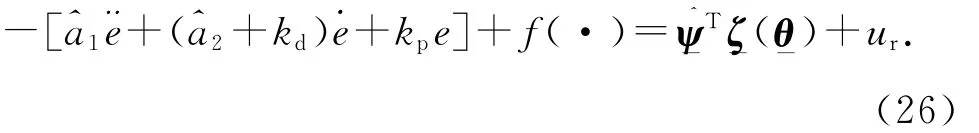
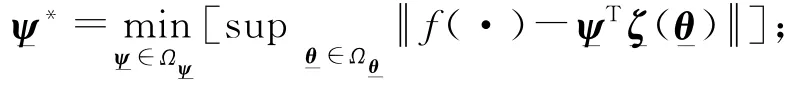
利用模糊系統逼近擾動函數f（·），有

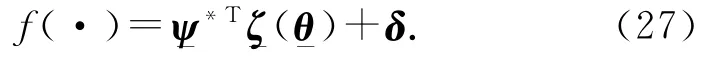
式中：Ψ-

*為參數Ψ-的最優估計值，

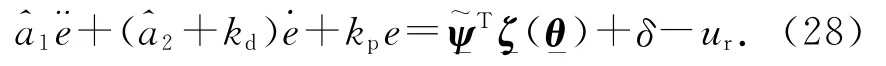
令

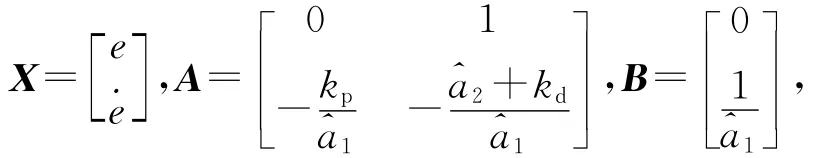
定義李雅普諾夫函數如下：

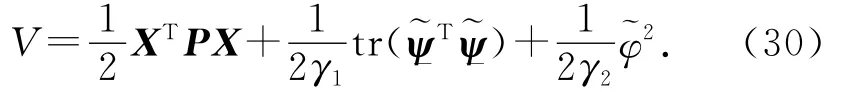
式中：γ1和γ2為學習系數，且γ1＞0，γ2＞0.將式（30）對時間進行求導：

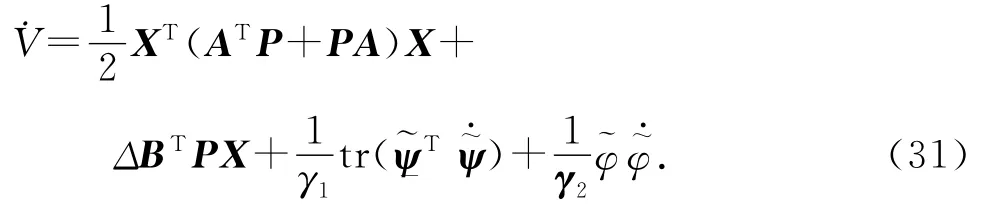
式中：ATP+PA=-Q，P、Q均為正定對稱矩陣[15]，取

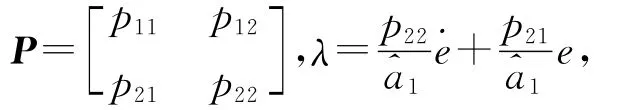
則ΔBTPX=Δλ.式（31）可以簡化為

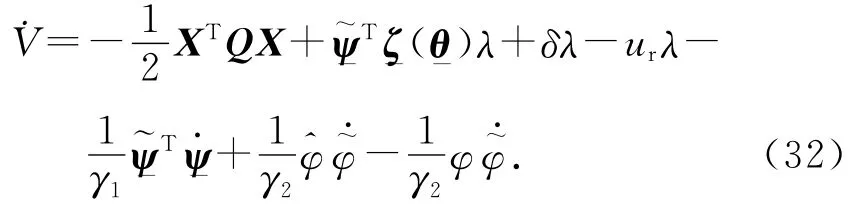
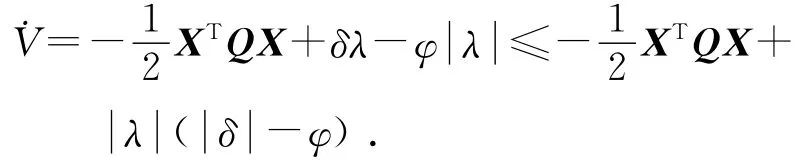
4 實驗研究

該實驗以搭載于某多旋翼無人機上的機載云臺穩定跟蹤控制系統作為研究對象，如圖4所示.

系統采用TMS320F28335作為處理器，整個控制周期為30 ms，采用光電編碼器作為位置傳感器，測量精度是±60″.采用集成了三軸陀螺儀和三軸加速度計的某傳感器作為速率傳感器和加速度傳感器.通過掃頻法辨識得到機載云臺模型的參數，激勵信號為掃頻信號，掃頻信號重復周期T=10 s.

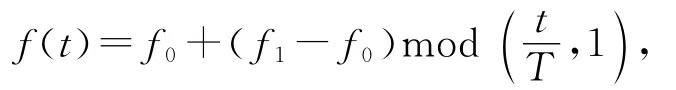
圖4 實驗用搭載于多旋翼無人機的機載云臺Fig.4 Airborne platform mounted on multi-rotor UAV for experiment

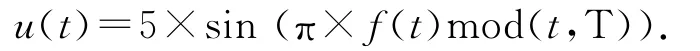
式中：f0=0，f1=10.得到的模型參數如表1所示.

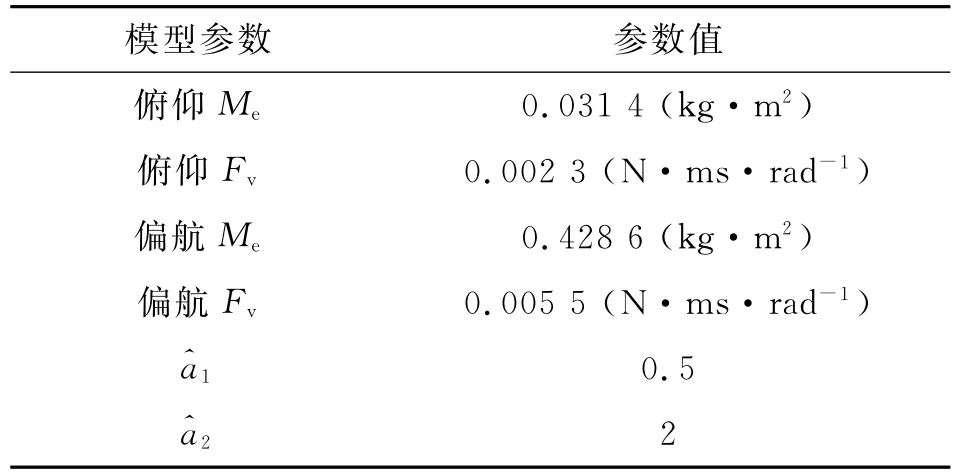
表1 機載云臺模型參數Tab.1 Parameters of airborne platform system

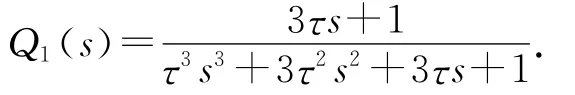
根據定理1可知，補償控制器Q2（s）=1-P（s）× Q1（s）=1-[C（s I-A）-1B]Q1（s）.將式（5）的A、B、C代入Q2（s），可得

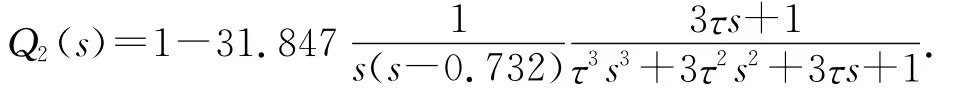
低通濾波器Q1（s）選擇典型的Q31濾波器，時間常數τ=0.01，低通濾波器為

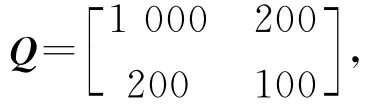
學習系數γ1=200，γ2=0.1，PD控制器參數：kp=15，kd=2，模糊控制系統模糊輸入角度θ的隸屬函數選取為：=exp（-（θ+1）2），= exp（-（θ+0.5）2）=exp（-（θ+0.0）2）= exp（-（θ-0.5）2=exp（-（θ-1）2）.模糊控制系統模糊輸入角速度˙θ的隸屬函數選取為= exp（-0.5（θ+8）2）=exp（-0.5（θ+4）2）= exp（-0.5（θ+0.0）2）=exp（-0.5（θ-4）2），μA52 =exp（-0.5（θ-8）2）.

根據圖2設計的擾動觀測器控制結構，以俯仰通道為例，飛行器在懸停狀態下，機載云臺的給定俯仰角度為0°，在兩種擾動觀測器結構下以100 Hz的采樣頻率，分別對俯仰方向上的位置傳感器進行采樣，獲取實際的角度信息.通過維持給定角度的對比分析，驗證本文提出的IVDOB控制結構抑制無人機載體擾動、維持視軸穩定的能力.如圖5（a）所示為采用VDOB后視軸的角度誤差曲線.圖中，A為視軸角度，角度誤差的最大值不超過0.8°，誤差均方值小于0.25°.如圖5（b）所示為采用IVDOB后視軸的角度誤差曲線，誤差均方值小于0.02°.本文提出的IVDOB結構相對VDOB具有更好的抑制載

對稱正定矩陣體擾動的能力和更高的視軸穩定精度.

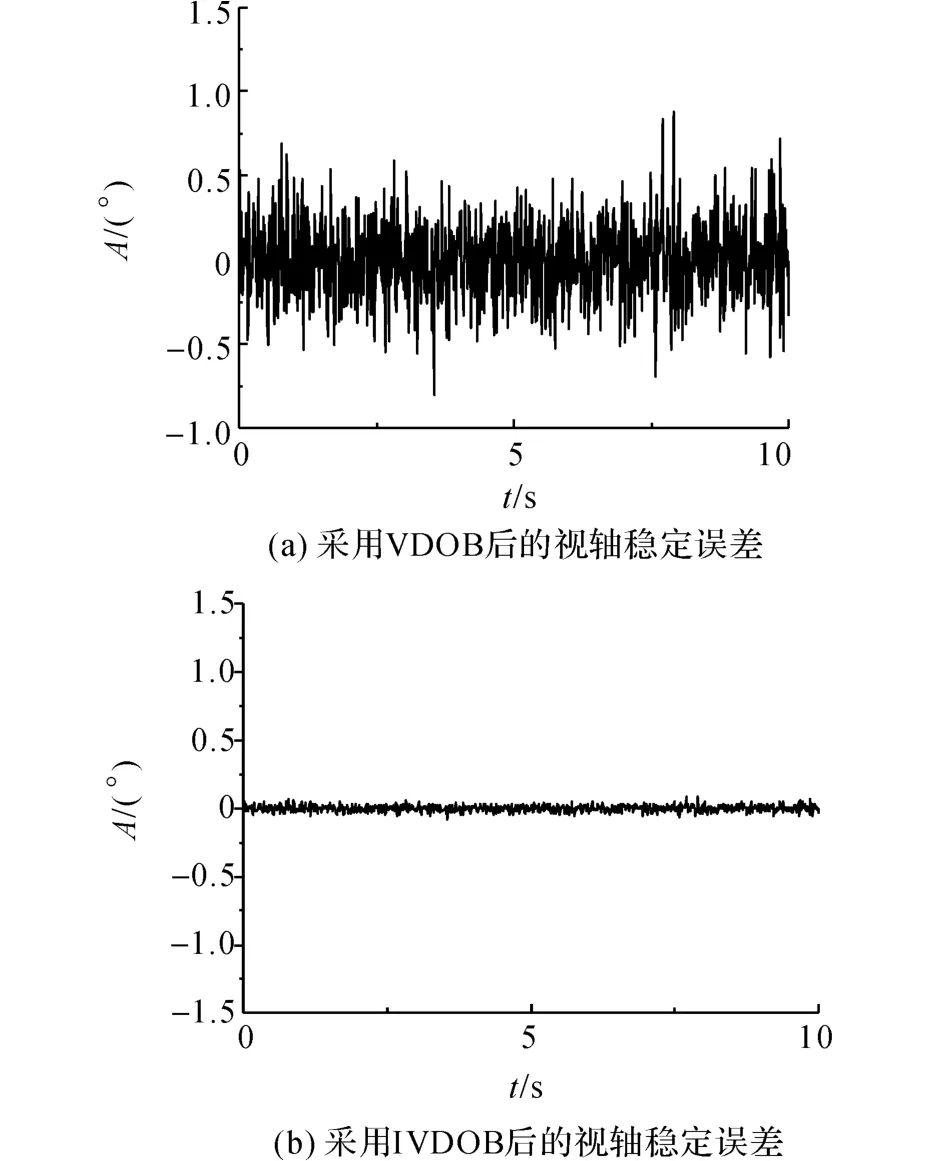
圖5 視軸穩定誤差對比結果Fig.5 Comparison results of line of sight error

根據圖3的設計控制系統，通過本文提出的模糊自適應控制結構對給定位置信號的跟蹤實驗，驗證該控制系統和對擾動的補償能力.實驗條件如下.在飛行過程中引入力矩擾動TD作為系統的未知擾動，如圖6所示，TD通過程序加入到控制器的輸出端，疊加幅值為1、信號周期為1 s的方波擾動信號Va.由于該信號與控制器沒有任何信息上的交換，可以模擬實現未知干擾的引入.

如圖7所示為模糊自適應控制對引入的力矩擾動TD的補償結果.控制器的輸出與擾動曲線基本一致，說明了模糊自適應控制器對力矩擾動良好的補償能力.模糊自適應控制器輸出曲線存在的振蕩主要是由于IVDOB未能完全補償機體擾動所致.

圖6 引入的力矩擾動Fig.6 Introduced torque disturbance

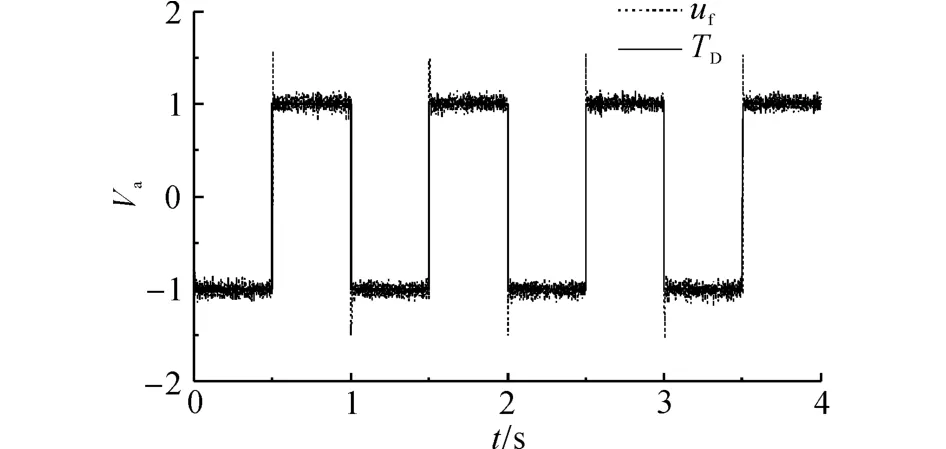
圖7 模糊自適應控制器補償TD的效果Fig.7 Result of torque disturbance rejected by fuzzy self-adjusting controller

如圖8所示為未引入模糊自適應控制器的跟蹤曲線及跟蹤誤差.可以看出，跟蹤誤差達到了0.2°，難以實現機載云臺對給定信號的精確跟蹤.如圖9（a）所示為采用本文提出控制方法對正弦信號的跟蹤曲線，跟蹤誤差的最大值不超過0.08°，且跟蹤誤差有界，如圖9（b）所示.顯然，本文提出的控制方法的跟蹤效果較理想，能夠精確地跟蹤給定位置信號.

如圖10所示為采用本文提出控制方法在外界風速約為3.2 m/s時對給定信號的跟蹤效果和跟蹤誤差曲線.可以看出，在外界有風干擾時能夠精確地跟蹤給定位置信號，在給定切換點處存在的誤差不超過0.8°，且基本不存在振蕩.在非切換處的誤差不超過0.1°.

圖8 未引入模糊控制器的跟蹤曲線和跟蹤誤差Fig.8 Tracking curve and tracking error without fuzzy self-adjusting controller

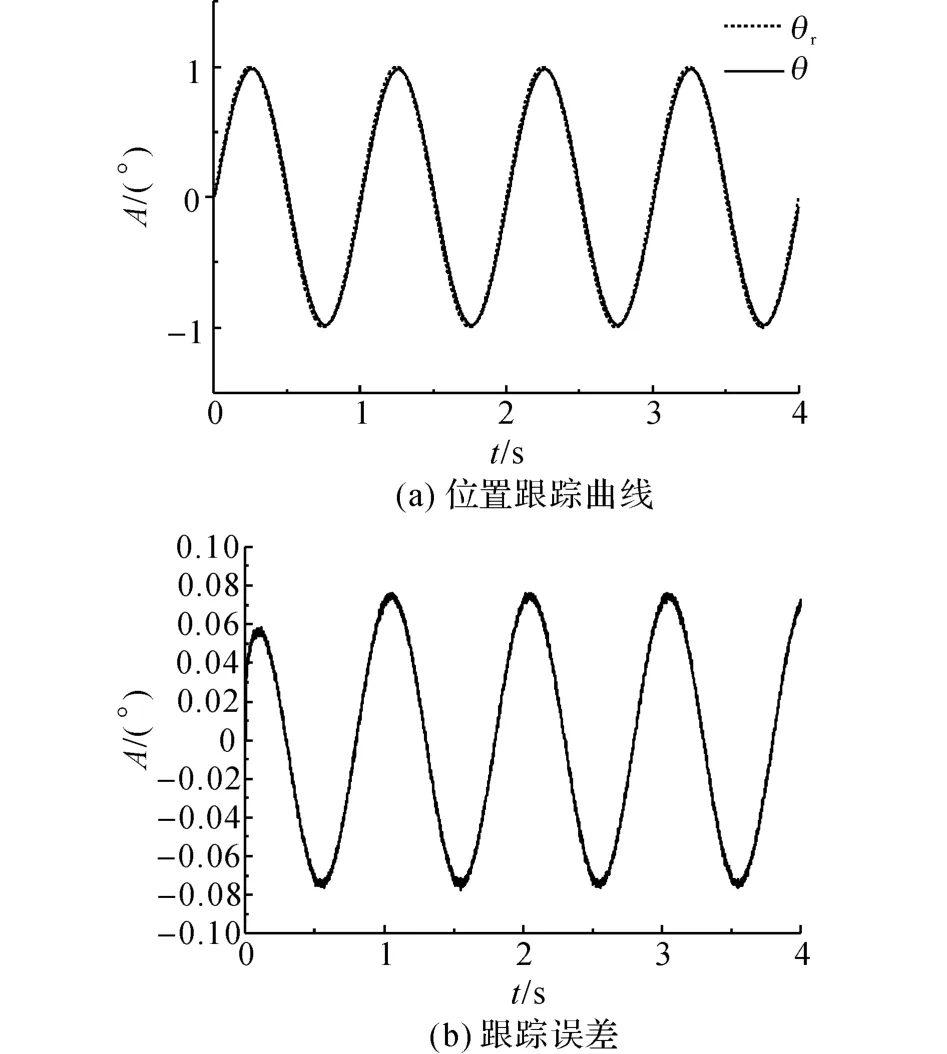
圖9 引入模糊自適應控制器的跟蹤曲線和跟蹤誤差Fig.9 Tracking curve and tracking error with fuzzy self-adjusting controller

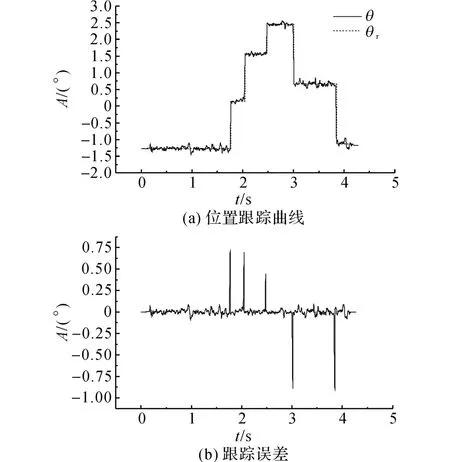
圖10 在外界有風時的跟蹤曲線和跟蹤誤差Fig.10 Tracking curve and tracking error of proposed method under wind condition

5 結 語

理論分析和機載飛行實驗均表明，在擾動觀測器結構中引入補償控制器Q2后，機載云臺的低頻擾動和高頻擾動均得到了很好的補償，視軸穩定誤差均方值小于0.02°，改進后的擾動觀測器補償擾動能力明顯提高.模糊自適應控制方法能夠逼近并補償機載云臺系統中的非線性未知擾動，對給定位置信號的跟蹤誤差小于0.08°，達到了機載云臺精確跟蹤的性能要求；同時，跟蹤誤差有界，系統漸進穩定，具有很好的穩定性和魯棒性.綜上所述，本文提出的控制方法完全滿足了多旋翼無人機機載云臺的穩定跟蹤控制的要求.

（

）：

[1]李迪.微型飛行器電子穩像技術研究[D].長春：中國科學院長春光學精密機械與物理研究所，2012.

LI Di.Study on electronic digital image stabilization technology for the image sequences of MAV[D].Changchun：Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，2012.

[2]MEI Y，ZHAO H Y，GUO S Y.The analysis of Image Stabilization technology based on small-UAV airborne video[C]∥Proceedings of IEEE International Conference on Computer Science and Electronics Engineering.Hangzhou：IEEE，2012：586-589.

[3]UMENO T，KANEKO T，HORI Y.Robust servo system design with two degrees of freedom and its application to novel motion control of robot manipulators[J].IEEE Transactions on Industrial Electronics，1993，40（5）：473-485.

[4]陸建山，王昌名，何云峰，等.改進型擾動干擾器在穩定平臺伺服系統中的應用[J].振動與沖擊，2013，32（8）：96-99.

LU Jian-shan，WANG Chang-ming，HE Yun-feng，et al.Application of improved disturbance observer in a stable platform servo system[J].Journal of vibration and Shock，2013，32（8）：96-99.

[5]任彥，劉正華，周銳.滑模干擾觀測器在低速光電跟蹤系統中的應用[J].北京航空航天大學學報，2013，39（6）：835-840.

REN Yan，LIU Zheng-hua，ZHOU Rui.Application of low speed opto-electronic tracking systems based on sliding mode disturbance observer[J].Journal of Beijing University of Aeronautics and Astronautics，2013，39（6）：835-840.

[6]李嘉全，丁策，孔德杰，等.基于速度信號的擾動觀測器及在光電穩定平臺的應用[J].光學精密工程，2011，19（5）：998-1004.

LI Jia-quan，DING Ce，KONG De-jie，et al.Velocity based disturbance observer and its application to photoelectric stabilized platform[J].Optics and PrecisionEngineering，2011，19（5）：988-1004.

[7]謝巍，何忠亮.采用改進型擾動觀測器的控制方法[J].控制理論與應用，2010，27（6）：65-700.

XIE Wei，HE Zhong-liang.Control method with improved disturbance observer[J].Control Theory and Application，2010，27（6）：695-700.

[8]高篙，徐曉霞，肖秦琨，等.機載光電跟蹤系統的模糊自適應控制[J].西安工業大學學報，2009，29（6）：565-569.

GAO Song，XU Xiao-xia，XIAO Qin-kun，et al.The research on fuzzy self-adjusting control of airborne electro-optical pointing and tracking systems[J].Journal of Xi’an Technological University，2009，29（6）：565-569.

[9]朱海榮，李奇，顧菊平，等.擾動補償的陀螺穩定平臺單神經元自適應PI控制[J].電機與控制學報，2012，16（3）：65-77.

ZHU Hai-rong，LI Qi，GU Ju-ping，et al.Single-neuron adaptive PI control of the gyro-stabilized platform based on disturbance compensation[J].Electric Machines and Control，2012，16（3）：65-77.

[10]KHALIL H K.Nonlinear system[M].3rd ed.New Jersey：Prentice Hall，2002：24.

[11]HU Hong-jie，YUE Jin-yu，ZHANG Ping.A control scheme based on RBF neural network for high-precision servo system[C]∥Proceedings of IEEE International Conference on Mechatronics and Automation.Xi＇an：IEEE，2010.

[12]MILLER R，MOOTY G，HILKERT J M.Gimbal system configurations and line-of-sight control techniques for small UAV applications[C]∥Airborne Intelligence，Surveillance，Reconnaissance（ISR）Systems and Applications X，871308.Baltimore：SPIE，2013.

[13]扈宏杰，王元哲.機載光電平臺的復合補償控制方法[J].光學精密工程，2012，20（6）：1272-1281.

HU Hong-jie，WANG Yuan-zhe.Composite compensation control scheme for airborne opto-electronic platform[J].Optics and Precision Engineering，2012，20（6）：1272-1281.

[14]劉金琨.先進PID控制及其MATLAB仿真[M].北京：電子工業出版社，2003：102-110.

[15]丁建強，任曉，盧亞平.計算機控制技術及其應用[M].北京：清華大學出版社，2012：108-120.

Fuzzy self-adjusting tracking control based on disturbance observer for airborne platform mounted on multi-rotor unmanned aerial vehicle

WANG Ri-jun1，2，BAI Yue1，XU Zhi-jun1，GONG Xun1，ZHANG Xin1，2，3，TIAN Yan-tao4

（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，Changchun130033，China；2.University of Chinese Academy of Science，Beijing100039，China；3.School of Electrical and Information Technology，Changchun Institute of Technology，Changchun130012，China；4.School of Telecommunication Engineering，Jilin University，Changchun130025，China）

A scheme of fuzzy self-adjusting tracking control based on an improved disturbance observer（DOB）was proposed in order to compensate disturbance and accomplish the stabilized tracking control for airborne platform mounted on multi-rotor unmanned aerial vehicle.A compensated control was introduced into feedback loop which is in the structure of original disturbance observer.An improved disturbance observer was constructed based on velocity signals.The ability of disturbance compensation and robustness were analyzed.A fuzzy self-adjusting tracking control structure was designed according to the approaching property of fuzzy system and Lyapunov stability theory.The stability of the tracking control structure was proved.The flight experiment results showed that the mean square error of line of sight was below0.02°and the error of tracking reference position was less than0.08°after applying the proposed scheme.Results demonstrate that the proposed scheme can completely satisfy the stabilized tracking control demand of airborne platform.The disturbance rejected ability was significantly improved after introducing the compensated control.The proposed control method possessed upper stabilized tracking accuracy.

multi-rotor unmanned aerial vehicle；airborne platform；disturbance observer；tracking control；fuzzy self-adjusting；stabilization

TP273

A

1008-973X（2015）10-2005-08

2014-08-26.浙江大學學報（工學版）網址：www.journals.zju.edu.cn/eng

國家自然科學基金資助項目（11372309，61304017）；院省專項資助項目（2014YSHZ004）.

王日俊（1982—），男，博士生，從事無人機載荷穩像技術的研究.ORCID：0000-0003-1576-0793.E-mail：wangrijun1982@126.com

白越，男，副研究員.E-mail：baiy@ciomp.ac.cn