什么是計算教學的有力支撐？

張瑩

“買文具”是北師版小學數學四年級上冊“除法”單元第一課時“除數是整十數的除法”的教學內容，是學生后續學習“三位數除以兩位數”筆算除法中試商、調商的重要基礎，主要借助除數是整十數的除法，探索除數是兩位數除法的計算過程，重點學習判斷商是幾位數（定位）的方法。在學習本課之前，我對學生進行前測：“你能計算出90÷30和100÷40的結果嗎？可以的話，請用盡量多的方法計算出來。”結果從學生的錯例中發現，學生對于商及余數意義的理解不夠深刻，豎式計算也還存在一定的問題。很多教師提高學生計算能力的“法寶”是多練，而我認為讓學生充分理解算理是教師在計算教學中最該下工夫的地方。與此同時，在教學實踐過程中，我感到運用數學模型，引導學生進行不同算法間的對比溝通是切實可行的方法之一。

一、通過必要的追問，引導學生感知算理

師（出示主題圖）：淘氣帶了80元錢，每個書包20元，問能買幾個書包？怎么列式？

生1：80÷20。

師：為什么要用除法列式？你是怎么想的？

生2：淘氣帶了80元錢，每個書包20元，用80÷20就是看80里面有幾個20，也就是能買幾個書包。

師：下面，請同學們用自己喜歡的方法表示出“80里面有幾個20”。

……

除法有包含除和等分除兩個重要模型，在此之前學生接觸更多的是等分除，而本節課要讓學生嘗試用包含除的方法去理解算理。因此，在上述教學中，我沒有滿足于學生能正確列式就可以了，而是進行追問：“為什么要用除法列式？你是怎么想的？”在學生說出包含除的含義后，我引導學生的思維從列式計算轉向了對算理的思考。

二、通過模型的支撐，引導學生理解算理

根據認知發展理論可知，四年級學生的思維以具體形象思維為主，再向抽象思維轉化。因此，為符合學生的認知規律，豐富學生的感性認識，提高課堂教學的有效性，課上在學生遇到“80÷20”這樣一個新知識點時，我為學生提供方格圖、小棒、紙幣等直觀模型進行輔助教學，更好地幫助學生理解算理、掌握算法。學生操作的這些模型不僅是現在用來理解算理的工具，而且也是日后用以回憶本知識點和鏈接其他相關新知識的重要抓手，這些模型還將為實現算法多樣化和發展學生的個性提供了支撐條件。學生的方法如下：

（1）20+20+20+20=80;

（2）80-20-20-20-20=0;

（3）因為8÷2=4，所以80÷20=4;

（4）20×（ ）=80，因為20×4=80，所以80÷20=4;

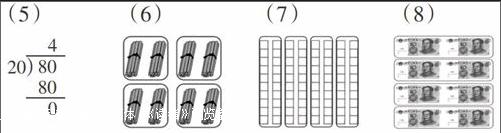
（5） ? ? ? ? ? ?（6） ? ? ? ? ? ? ?（7） ? ? ? ? ? ? ?（8）

■

在教學過程中，教師應關注學生的個性發展，積極創造條件讓學生親歷建構數學模型的過程，并鼓勵解決問題的策略和算法多樣化，使不同層次的學生在課堂上都能有所得。

三、通過對比溝通，引導學生深化算理

無論是前測的結果顯示，還是從課堂的實際情況來看，我發現學生在利用模型解決問題的過程中都沒有出錯，但用豎式進行計算時則有各種不同的錯誤出現。通過分析，我認為豎式計算的過程與學生擺小棒、分紙幣和圈格子圖所經歷的思維過程其實是一樣的，都是一個分的過程，然而學生的寫豎式由于比模型更為抽象，同時缺乏橫向的對比溝通，因此導致計算過程錯漏百出。

1.不同算法間的對比溝通

如果教師只是為了讓學生用模型而用模型，將模型操作與豎式計算當成兩個不相干的活動，忽視兩者之間的聯系，那么“讓學生親歷建模的過程，積累數學活動經驗”就成了一句空話，模型在計算教學中存在的意義也會極大的下降。因此，為了提高課堂教學效率，較好地幫助學生降低學習抽象知識的難度，我引導學生對不同的算法進行對比溝通，逐漸形成具體模型與抽象算式之間的聯系，使學生在計算時頭腦中有直觀模型作支撐。如課堂上，在學生把計算80÷20的各種方法在黑板上展示之后，我問學生：“剛才同學們用不同的方法計算出了結果，下面我們看看，大家都是在哪找到80的？”大部分學生都能順利地找出80根小棒、80元錢、80個小方格和橫豎式中的80。我繼續追問：“這些不同地方的80，有什么聯系？”學生回答：“表示淘氣帶了80元錢。”我繼續引導學生找出20，很快學生也都找出了2捆小棒、2張10元錢、2列方格和橫豎式中的20。我繼續問學生：“20表示什么？”學生在我的引導下回答出了“表示一個書包20元錢”的正確答案。我乘勢追問：“大家看看，4在哪？”在一生指黑板上橫豎式中的4及圈出小棒圖、方格圖和錢幣圖中的4份后，我問道：“所有的這些4，其實都可以用來表示什么？”學生水到渠成地回答出：“表示可以買4個書包。”……在這個環節中，我通過不斷的追問，引導學生進行不同算法之間的對比溝通，使學生在討論和辨析中，逐步地感受到算法形式上的多樣化和算理本質上的同一性。

2.不同錯誤間的對比溝通

在學習過程中，學生不可避免地會因為一些認知上的偏差，導致出現這樣或那樣的錯誤。這時教師不應簡單地予以否定，而是讓學生的思維過程得以充分展現，從中發現學生出現此類錯誤的原因，并加以針對性的指導，使學生的錯誤變成為課堂中寶貴的教學資源。因此，對于學生在學習過程中產生的錯誤，教師要有一定的預設性，并根據課堂上學生的實際情況，盡可能多地將各種錯誤和正確方法在同一時間內展現在學生面前，引導學生經歷一個自我辨析、糾錯、改正和提高的過程，從而有利于學生更加牢固地掌握所學的知識。如學生嘗試獨立完成80÷20的豎式計算時，我在課堂巡視中發現了以下四種豎式寫法，于是將它們展示到黑板上。

（1） ? ? ? ? ? ? ?（2） ? ? ? ? ? ? （3） ? ? ? ? ? ?（4）

■

師：請大家仔細觀察這些同學寫的豎式，選擇其中一個，說說你的想法。

生1：第（3）個豎式肯定不對，怎么可能商的個位上是空的，而十位上卻有數字？個位上是空的表示沒有，就要用0來占位，那么商就成了40，難道80里面有40個20嗎？所以，我認為應該把4寫在商的個位，這樣才能表示80里面有4個20。

生2：我認為第（4）個豎式也不對。淘氣帶了80元錢，每個書包20元，最后的結果只能是買4個書包，而不是40個書包，所以商4應寫在個位上。

生3：第（1）個豎式也不對，這里的商雖然是寫在個位上了，可是被除數80下面的數應該是80，而不是8。

生4：第（4）個豎式下面寫得也不對，因為它是除數和商相乘得到的，除數是20，商是4，20×4=80，所以應該是80，而不是8。

師：那你知道這個80表示的是什么意思嗎？

生5：這里的80表示買4個書包共花了80元錢。

師：通過剛才的討論，我們找到了正確的豎式，應該是——

生（異口同聲）：第（2）個算式！

……

上述教學中，學生出錯后，我并沒有急于指正或批評，而是把學生的各類錯誤和正確的寫法放在一起，讓學生在對比中進行自我辨析和自我糾錯。這樣，算理就在學生的互相討論和質疑中越辯越明，算法也越辯越清。

通過本節課的教學，我感受最深的是，不僅僅要在計算教學中使用模型，還要加強模型與算式之間的溝通，形成方法間的對比，才能成為計算教學中的有力支撐，更好地幫助學生理解算理。總結本次教學，是在以學生發展為本、以學生為主體的教學理念下，通過追問感知、理解算理、對比溝通三個步驟，使學生對除數是整十數除法的算理有初步的認識和理解，并引導學生進行專門的練習和更進一步的算法糾正，從而實現預設的教學目標。

（責編 藍 天）endprint