Matlab 在高職數學教學中的應用

遼寧省交通高等專科學校 勾麗杰

Matlab 在高職數學教學中的應用

遼寧省交通高等專科學校 勾麗杰

本文主要介紹Matlab在微積分計算方面的應用，提高學生掌握運用現代化的計算工具進行數學運算的基本技能，使課堂教學更加直觀、生動、形象。

高職數學教學 Matlab軟件 應用能力培養 數學技能

一、Matlab的特點

Matlab是MATrix LABoratory（矩陣實驗室）的縮寫，是由MathWorks公司于1984年推出的工程計算軟件。MATLAB具有強大的計算能力和數據可視化能力，它提供的工具箱能夠解決科學與工程計算中的大多數數學問題。Matlab目前已廣泛地應用于教學和科研領域，它的引入對于學生以后的工作也會大有幫助。本文著重介紹Matlab 在微積分計算及繪制圖形方面的應用。

二、Matlab在微積分計算中的應用

1. 用Matlab求函數極限。用Matlab求函數極限的基本語句：

（1）sym．創建一個符號變量．

（2）limit(f,x,a)．對于符號函數f，求當變量x趨于a時的極限值．

（3）limit(f,x,a,’right’)，右極限．

（4）limit(f,x,a,’left’)，左極限．

（5）limit(f,x,a,’inf’)，無窮極限．

例1，求下函數的極限。

程

syms x

f='x*(1/4*pi-atan(x/(1+x)))';

limf=limit(f,x,inf);

limf=simple(limf)

運行結果

limf =

1/2

2.用Matlab求一元函數的導數

用Matlab求函數導數的基本語句：

diff(f,v,n)． 函數f中對符號變量v求n階導數。當變量v和階次n省略時，表示對單變量的函數求一階導數。

例2 ， 求下函數的導數。

（1）y=e-x（x2-2x+3），求y'；

（2）y=sin2x·sin(x2)，求y"。

程序

syms x

y1=diff('exp(x)*(x^2-2*x+3)');

y2=diff('(sin(x))^2*sin(x^2)',2);

y1=simple(y1)

y2=simple(y2)

運行結果

y1 =

exp(x)*(x^2+1)

y2 =

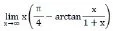
3.用Matlab求函數的最值與極值

用Matlab求函數的最值與極值的基本命令見表1。

表1 求函數的最值與極值的基本命令

例3，求f(x)=x3+x2-x-1在[-2,2]內的最大值與最小值、極大與極小值以及零點。

先求函數的最值

程序

syms x y

f='x^3+x^2-x-1';

x1=fminbnd(f,-2,2)

x2=fminbnd(‘-x^3-x^2+x+1’,-2,2)

x=x1;minf=eval(f)

x=x2;maxf=eval(f)

運行結果

x1 =

-2

x2 =

2

minf =

-3

maxf =

9

再求函數的零點

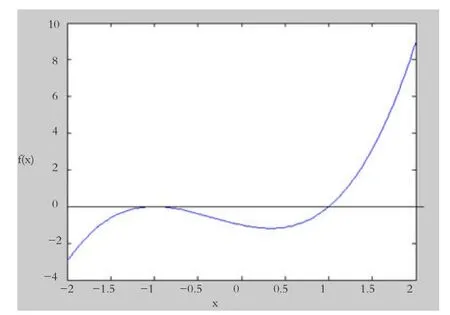
可以先在區間[-2,2]做它的圖形，如上圖所示。

程序

f='x.^3+x.^2-x-1'

x=-2∶0.0001∶2

fplot(f,[-2,2])

xlabel(‘x’)

ylabel(‘f(x)’)

運行結果

從圖形中可以看出，在[-2,2]上大概有兩個零點，于是程序

f='x.^3+x.^2-x-1'

x1=fzero(f,[-2，2])

x2=fzero(f,[0,2])

運行結果

f =

x.^3+x.^2-x-1

x1 =

-1

x2 =

1

即，此函數在點x=-1和x=1處各有一個零點。

第三求函數的極值。從圖1中可以看出，函數在區間[-2,0]處有極大值，在區間[0,2]處有極小值，所以可進行如下操作：

>> f=’x^3+x^2-x-1’

f =

x^3+x^2-x-1

>> df=diff(f)

df =

3*x^2+2*x-1

>> df=’3*x^2+2*x-1’

df =

3*x^2+2*x-1

>> x1=fzero(df,[-2,0])

x1 =

-1

>> x2=fzero(df,[0,2])

x2 =

0.3333

>> x=x1;maxf=eval(f)

maxf =

0

>> x=x2;minf=eval(f)

minf =

-1.1852

也可以用x=solve(‘3*x^2+2*x-1=0’)求駐點。

2.4 用Matlab求函數的積分

用Matlab求函數的積分的基本命令見表2。．

表2 求函數的積分的基本命令

例4，f(x)=2a3sinx。

程序

Syms x a

f='a*x^3*sin(x^2)'

y1=int(f);%對x的不定積分

y2=int(f,a); %對a的不定積分

y3=int(f,0,2*pi);%對x在給定區間(0,2pi)上的定積分

y1=simple(y1) %將積分結果化簡

y2=simple(y2) %將積分結果化簡

y3=simple(y3) %將積分結果化簡

運行結果

f =

a*x^3*sin(x^2)

y1 =

-1/2*a*(-sin(x^2)+x^2*cos(x^2))

y2 =

1/2*a^2*x^3*sin(x^2)

y3 =

1/2*a*sin(4*pi^2)-2*a*pi^2*cos(4*pi^2)

三、結束語

引進最新版本Matlab數學軟件可以提高學生利用計算機及數學軟件求解問題及建立數學模型的能力，更好地體現高職教育的教學特色。

[1]勾麗杰．應用高等數學[M]．北京:高等教育出版社，2013

[2]勾麗杰．MathCAD在高職數學教學中的應用[J]．遼寧經濟管理干部學院學報，2010

ISSN2095-6711/Z01-2015-04-0225