基于合理遺忘歷史樣本的房地產價格非線性預測

周子英

(湖南工程學院 管理學院，湖南 湘潭 411104)

0 引言

房地產價格受到房地產供給、需求以及預期等多種因素的影響，其價格的走勢存在一定的規律性[1]。近年來，由于中國的經濟、城鎮化速度大力推進，導致房地產價格處于不斷上漲的態勢。由于房地產作為一種商品，必然受到供求關系的影響，此外，房地產作為一種生活的必須品，再加上其又具有保值增值的特性，具有一定的投資性，對消費者的心理預期影響較大，因此，房地產價格預測受到了越來越多人的關注[2]。

針對房地產價格預測問題，國內外專家進行了大量研究，提出許多房地產價格預測方法。傳統房地產價格預測基于多元回歸預測法進行建模，該方法簡單、易實現，但難以準確描述房地產價格的時變性、非平穩性，預測結果不理想[2,3]。房地產價格受到多種因素影響，具有混沌性和周期性，為此，一些學者提出了基于神經網絡、貝葉斯網絡、隱馬爾科夫鏈、支持向量機等非線性的房地產價格預測模型，獲得比較理想的預測結果[4-7]。其中極限學習機(extreme learning machine，ELM)是一種新型的前饋神經網絡，根據Moore-Penrose廣義逆矩陣理論，將訓練迭代轉化為線性方程組求解，一次可完成網絡訓練，而傳統神經網絡需要多次迭代過程確定網絡輸出權值，因此，ELM大幅度提高了網絡預測建模效率[8]。房地產價格歷史數據是一種典型的時間序列數據，數據間具有明顯的時序關聯性，同時，由于房地產價格數據具有非線性、時變性，隨著新的輸入、輸出數據不斷得到新的數據，房地產價格在不斷地變化，為了使模型能準確地反映出房地產價格，就要用新的數據描述模型，而與當前狀態相關性較小的舊數據可以忽略或所占的比重應降低；同時根據“近大遠小”的原理(距離預測部分近的信息對未來預測結果影響更大)，為此，需要對訓練樣本進行合理選擇，選擇與預測點關聯比較強的歷史樣本進行房地產價格建模與預測。為此，有學者提出利用在線貫序極限學習機(OS-ELM)進行時間預測預測，在預測時，首先在初始訓練階段計算出ELM神經網絡的初始網絡權值，然后隨首新的訓練樣本的加入，網絡權值亦可以在初始網絡權值的基礎上進行遞推[9,10]。由于OS-ELM模型假設新、舊訓練樣本對時間序列數據的預測結果具有同等程度的重要性，采用等權處理，難以準確反映不同訓練樣本對預測結果的不同影響；再者，OS-ELM模型只要獲得新訓練樣本，就會機械的更新網絡輸出權值，缺乏靈活性，增加了不必要的計算量[11]。

為了提高房地產價格的預測精度，針對房地產價格時間序列的特殊性，提出了一種基于合理遺忘歷史樣本的房地產價格預測模型(ELM，RF-ELM)，并通過房地產價格仿真實驗對模型的預測性能加以驗證。

1 在線貫序極限學習機(OS-ELM)

前饋神經網絡采用梯度下降算法調整網絡權重，存在學習速度慢、易陷入局部最小值、出現過度訓練等缺陷，針對這些問題，Huang等根據摩爾-彭羅斯(MP)廣義逆矩陣理論提出了極限學習機(ELM)算法，該算法可以通過一步計算就可以解析出網絡的權值，極大的是高了網絡的計算速度和泛化能力。設收集的訓練集為：表示重構后的間序列，τ為延遲時間，m為相空間重構的嵌入維數，那么基于ELM的預測模型為：

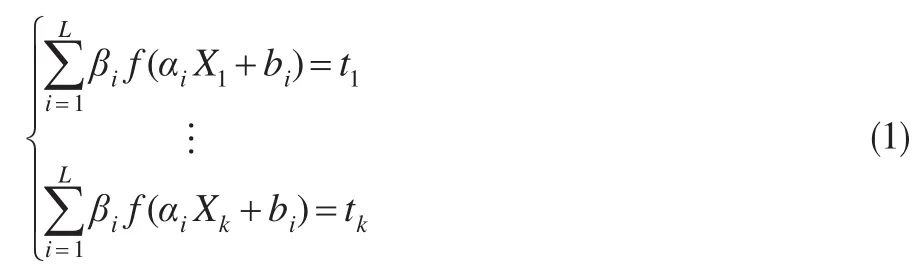
式中，αi為連接第i個神經元的輸入權值；bi為第i個神經元的偏差；k表示訓練集的樣本數；βi為第i個神經元的輸出權值。

采用矩陣形式將式(1)變為：

式中，Tk為輸出向量；βk為輸出權值；Hk為神經元矩陣，表示如下：

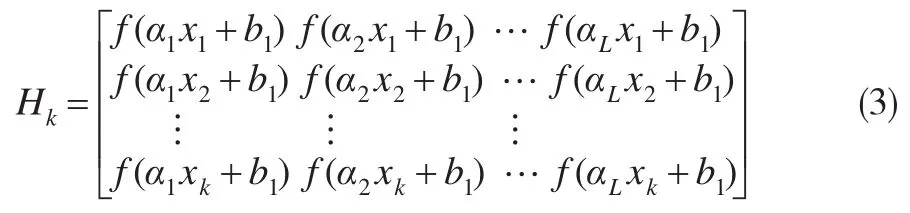
對式(2)進行求解得到如下輸出權值：

通過以上輸出權值，可得訓練后的ELM預測模型為：

式中，t和x分別為模型的輸入和輸出。

ELM是一種離線學習算法，難以對訓練樣本進行合理選擇學習，為此，學者提出了在線貫序極限學習機(OS-ELM)，算法具體步驟如下：

（1）：在滿足K≥L的條件下，根據時間序列Sk計算預測模型的初始輸出權值：

（2）：設獲得新的訓練樣本(xk+1,tk+1)，那么可以將它組合到訓練集中，然后根據式(6)計算輸出權值Pk+1與βk+1：

式 中 ，hk+1=[f(α1xk+1+b1)f(α2xk+1+b2) …f(αLxk+1+bl)]

（3）：訓練集的樣本數加1，并跳轉到step2。

（4）：不斷重復上述步驟，直到所有訓練集樣本均參加訓練為止。

2 RF-ELM的房地產價格預測模型

2.1 RF-ELM模型

為解決OS-ELM在房地產價格預測時存在的不足，提出一種基于合理遺忘選擇歷史樣本的房地產價格模型(RF-ELM)。假設當前訓練集包含k個房地產價格樣本：(x1,t1)，(x2,t2)，…，(xk,tk)，根據式(4)計算輸出權值βk，如果有新的房地產價格訓練樣本(xk+1,tk+1)加入到訓練集時，那么輸出權值βk+1計算公式為：

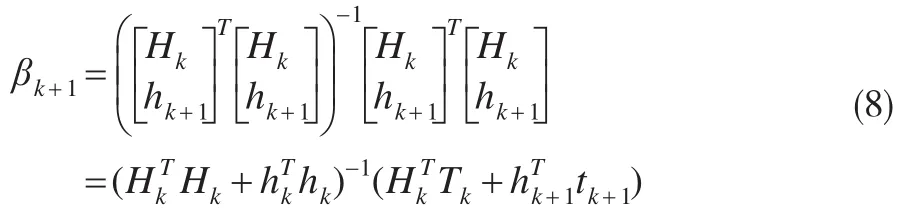
式中，輸出權值βk+1的都由舊的房地產價格訓練集構成，需要對它們進行加權，這樣式(8)變成為：

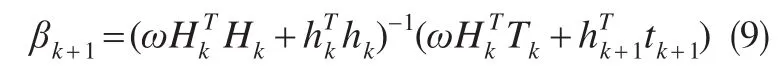
式中，ω為遺忘因子。

通過引入ω，減弱舊訓練樣本對預測結果影響，當ω值過小時，那么相對應的舊訓練樣本就被丟棄，新訓練樣本對預測結果影響間接增強。令

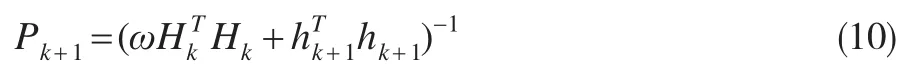
對(9)式兩端同時求逆可得：

將式(11)代入式(9)，輸出權值βk的遞推更新方式為：

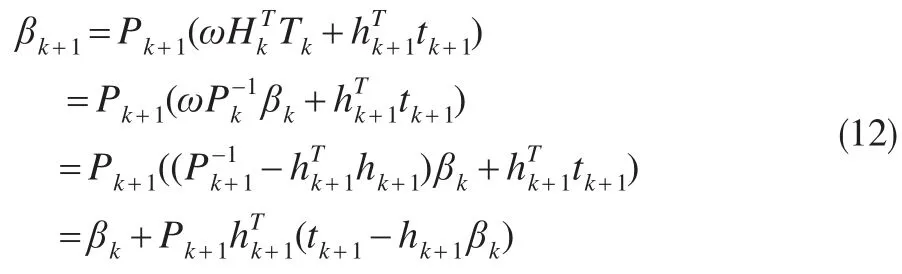
在式(9)引入Sherman-Morrison矩陣進行求逆，Pk的遞推更新方式為：

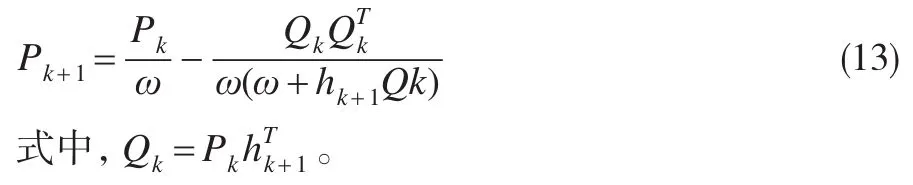
2.2 RF-ELM的房地產價格預測步驟

(1)選擇房地產價格時間序列的最佳延遲時間(τ)和嵌入維數(n)，那么房地產價格時間序列x1,x2,…,xN轉化為訓練樣本為輸入向量，ti=xi+n為輸出向量，K=N-n≥L。

(2)根據(X1,t1)，(X2,t2)，…，(Xk,tk)計算初始輸出權值：

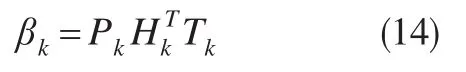
式中，C為嶺回歸系數；Ik為單位矩陣；

(3)將Xk+1=[xN-n+1,xN-n+2,…xN]T作為極限學習機的輸入，計算神經元矩陣輸入向量hk1，得到房地產價格樣本xN+1的一步預測值：

(4)當采集到房地產價格樣本xN+1的實際值后，首先根據式(7)對Pk進行選擇性更新：

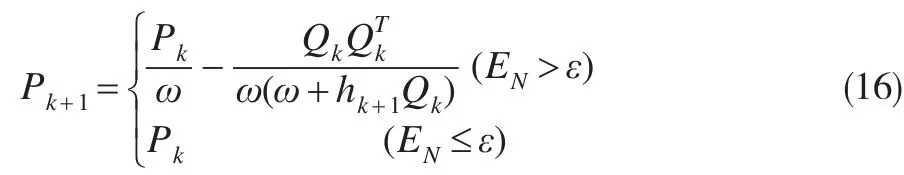
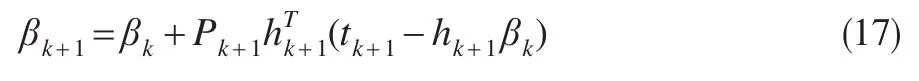
式中，tk+1=xN+1

(5)房地產價格訓練集的樣本數加1，并跳轉到步驟(3)，直到所有訓練樣本訓練完為止。

3 仿真實驗

3.1 源數據

選取中國房屋銷售價格指數月度數據進行實證分析，數據來源于中經網統計數據庫1998年10月到2011年12月的房地產價格，共收集到158個數據點，具體如圖1所示。

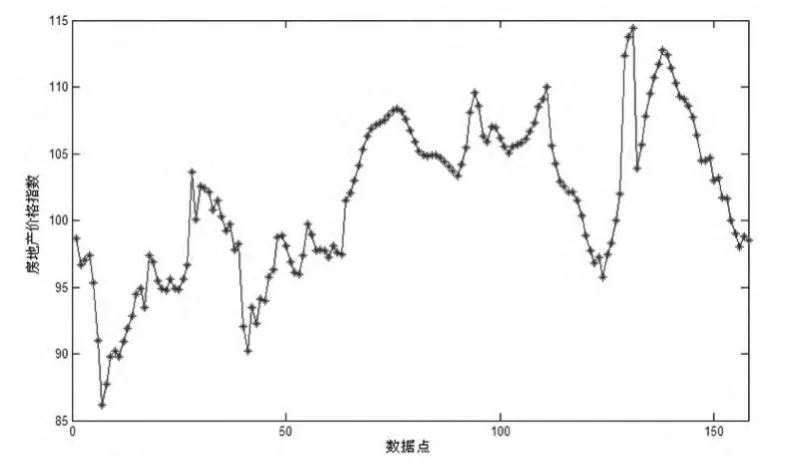
圖1 收集的房地產價格數據

3.2 對比模型及評價標準

為了使RF-ELM的房地產價格預測結果具有可比性，選擇OS-ELM、ELM作為對比模型。采用均方根誤差(RMSE)和平均相對百分比誤差(MPAE)作為模型的評價標準，分別定義如下：

3.3 學習樣本的構造

3.3.1 選擇時間延遲

首先采用采用互信息法進行時間延遲(τ)的計算，如圖2所示。從圖2可知，當τ=4時，互信息函數達到第一極小值，所以房地產價格時間序列的最佳時間延遲為τ=4。

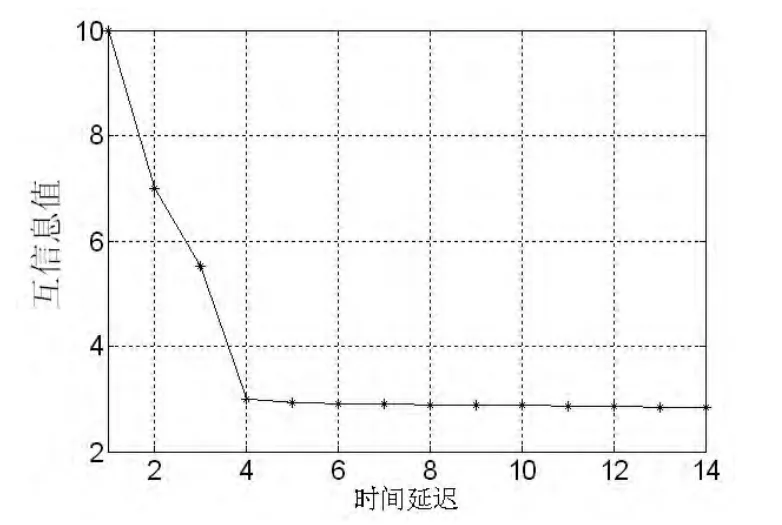
圖2 時間延遲(τ)的計算

3.3.2 嵌入維數確定

(1)根據互信息法求出τ=4，將嵌入維數的初值設為m=1。

(2)選擇合適的臨界距離r，根據式(20)計算Cn(r)，向量距離采用∞范數計算，即兩個向量最大分量差作為向量距離。

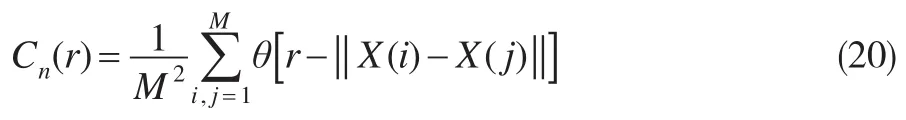
式中，r表示臨界距離的大小；M表示相點的個數；θ表示Heaviside單位函數。

(3)采用最小二乘法對logC(r)n～logr曲線中的直線段進行擬合，得到直線的斜率D，此時，D表示關聯維數。

(4)為了獲得最佳嵌入維數，將m值進行累加，返回步驟(2)。

依據以上步驟進行嵌入維數的求取，得到不同嵌入維數下的關聯維數變化曲線如圖5所示。從圖5可知，當m=5時，關聯維數已達到飽和狀態，說明房地產價格時間序列的m=5。

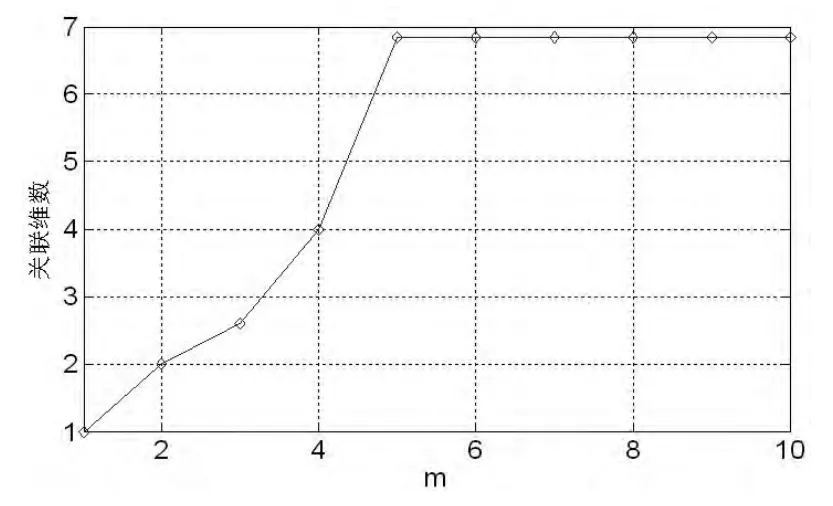
圖3 嵌入維數(m)的計算

采用最佳參數τ=4，m=5對房地產價格序列進行重構，然后將重構后的訓練集輸入RF-ELM模型進行訓練，建立最優房地產價格預測模型，并對測試集進行預測。

3.4 結果與分析

3.4.1 房地產價格單步預測性能對比

RF-ELM參數為：遺忘因子ω=0.55，閾值ε=0.001，嶺回歸系數C=80，然后將訓練集輸入RF-FLM進行訓練，最后對測試集進行單步預測，房地產價格預測結果和預測絕對誤差如圖3所示。從圖3可知，房地產價格預測值與實際值之間十分接近，RMSE為1.84，MAPE%為1.06，由此可以看出利用RF-ELM模型進行房地產價格預測可以獲得較高的預測精度。

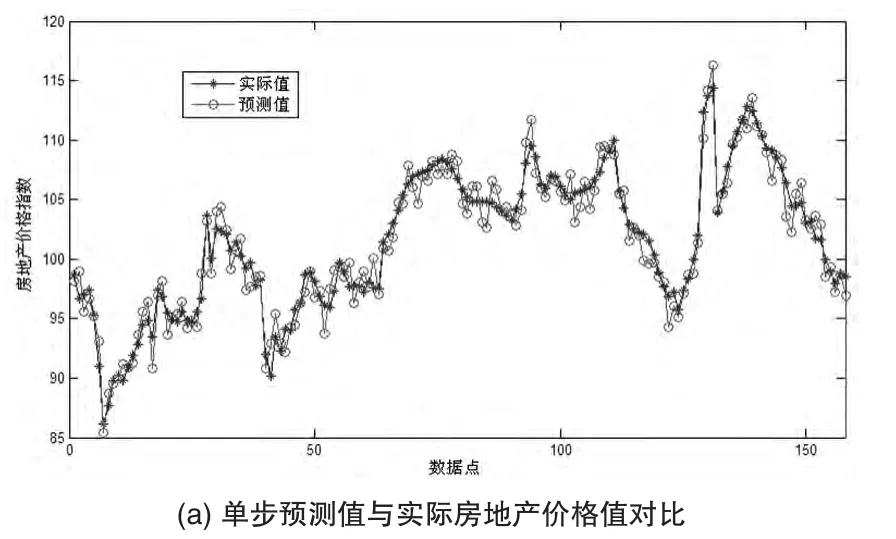
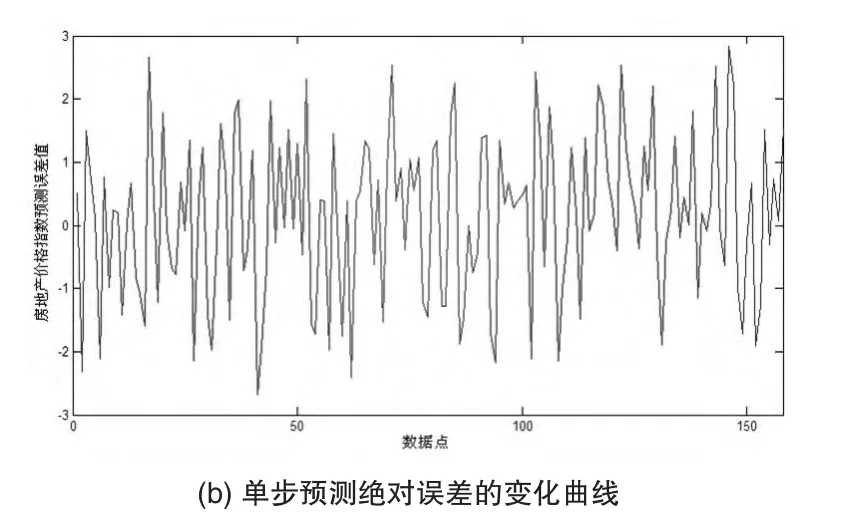
圖3 RF-ELM的單步預測性能

3.4.2 房地產價格多步預測性能對比

房地產價格預測的目標就是對房地產價格變化趨勢進行把握，因此要求有一定提前預測時間，采用單步預測法對房地產價格投資決策實際應用價值不大，因此需要將單頻預測擴展到多步預測。采用RF-ELM、OS-ELM和ELM對房地產價格進行建模與預測，2步、4步和6步預測結果的RMSE和MAPE%如表1所示。

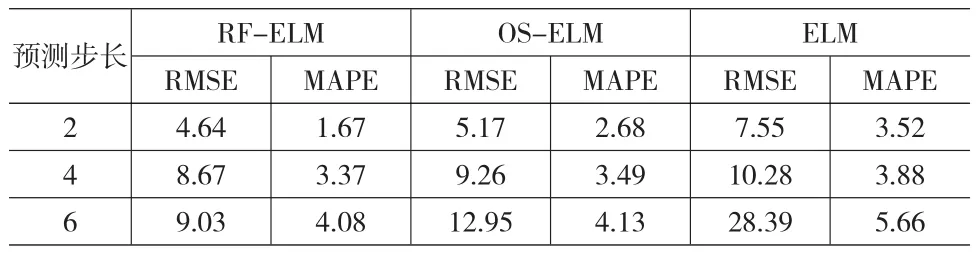
表1 3種房地產價格預測模型的預測誤差對比

對表1中3個模型在不同預測步長的性能進行分析，可以得到如下結論：

(1)傳統極限學習機(ELM)在初始訓練階段完成后，網絡輸出權值不再發生改變，隨著房地產價格預測步長逐漸增大，訓練集與當前時刻間房地產價格預測點的距離越大，建立預測模型不能難以準確刻畫當前時刻的房地產價格動態變化特性，房地產價格的預測精度比較低。

(2)相對于ELM，由于RF-ELM和OS-ELM不斷利用新采集的房地產價格訓練樣本對預測模型進行在線更新，預測誤差明顯減小，此外，由于新采集的房地產價格訓練樣本與預測點間的距離最小，可以準確跟蹤房地產價格動態變趨勢，獲得的房地產價格預測結果更加可靠。

(3)相對于OS-ELM，RF-ELM的預測誤差更小，主要由于OS-ELM模型將距離房地產價格較遠的房地產價格訓練樣本同等對待，然而，現實情況卻是房地產與當前較近的時間點的房地產價格呈十分緊密的聯系，而OS-ELM模型將所有的訓練樣本賦予同樣的權重，難以準確反映房地產價格之間的時間相關性。而RF-ELM以遺忘舊訓練樣本的方式，對一些距離預測點較遠，關聯性較小的樣本賦予較小的權值，將無用的樣本數據點丟棄，突出了新的房地產價格訓練樣本對預測點影響，可以較好的捕捉真實房地產價格變化特性，從而可以獲得了令人滿意的預測效果。

3.3.3 其他房地產價格的預測

為了進一步測試本文模型的普適性，采用2000年1月到2012年8月長沙市房地產價格、2001年3月到2012年8月武漢市房地產價格、2002年5月2013年3月深圳市房地產價格、2003年2月到2012年11月湘潭市房地產價格進行仿真測試，得到相應預測結果，預測誤差見表2。

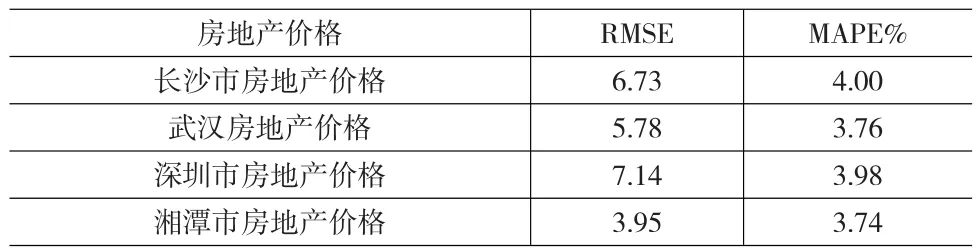
表3 其它城市房地產價格預測精度

從表2可知，利用RF-ELM進行各地房地產價預測，均獲得了較好的預測精度，長沙市房地產價格的RMSE、MAPE分別為6.73和4.00，其余三地的房地產價格預測值的MAPE均小于4.00，都具有較高的預測精度，結果表明，因此，RF-ELM是一種預測精度高的房地產價格預測模型。

4 結束語

為了提高房地產價格的預測精度，針對房地產價格訓練樣本選擇問題，提出了一種基于合理遺忘歷史樣本的房地產價格預測模型。仿真結果表明，相對對比模型，RF-ELM提高了房地產價格的預測精度，加快了訓練速度，可以更好的滿足房地產價格在線預測要求。由于房地產價格是受政治、經濟、供給、需求等多種因子的影響，本研究只房地產價格歷史時間序列數據，沒有考慮到這些因素的影響，綜合考慮多種因子對房地產價格的影響，有待進一步研究。

[1]章晨,鄭循剛,龔沁.基于ARMA模型的我國房地產價格預測分析[J].生產力研究2012,(2).

[2]柳冬,王雯珺,汪壽陽.我國房地產價格影響要素分析與趨勢預測[J].經濟與金融,201,22(5).

[3]楊勵雅,邵春福.基于BP神經網絡與馬爾可夫鏈的城市軌道交通周邊房地產價格的組合預測方法[J].吉林大學學報(工學版),2008,38(3).

[4]周亮,周正.基于時間序列的房地產價格指數預測方法探討[J].哈爾濱商業大學學報(社會科學版),2008,(2).

[5]李萬慶,張金水,孟文清.基于小波神經網絡的房地產價格指數預測研究[J].河北工業大學學報(自然科學版)[J].2008,25(1).

[6]梁坤,聶會星,徐樅巍.基于支持向量機的北京市房地產價格指數預測[J].合肥工業大學學報,2011,34(4).

[7]鐘昌寶.基于灰色-馬爾柯夫模型預測房地產價格[J].統計與決策,2005,(1).

[8]胡曉龍,郜振華,馬光紅.基于Elman神經網絡的房地產價格預測[J].統計與決策,2008,(7)．

[9]Callado A,Keu R J,Sadok D,et a1.Better Network Traffic Identification Through The Independent Combination of Techniques[J].Journal of Network and Computer Applications,2012,33(4).

[10]高光勇,蔣國平.采用優化極限學習機的多變量混沌時間序列預測[J].物理學報,2012,61(4).

[11]張弦,王宏力.基于貫序正則極端學習機的時間序列預測及應用[J].航空學報,2011,32(7).