教育對經濟增長貢獻率估算方法的比較

王小婷，崔玉平

(1.蘇州大學 教育學院，江蘇 蘇州 215123；2.滁州學院 學生處，安徽 滁州 239000)

0 引言

近些年，有關教育亦或是高等教育對經濟增長貢獻的定量研究一直倍受關注。教育對經濟增長貢獻估算主要基于兩個角度，一是教育對國民收入增長額的貢獻率，二是教育對國民經濟增長速度的貢獻率。對于前者，研究方法主要有舒爾茨的教育投資收益率估算方法、勞動力質量修正法等；對于后者，研究方法集中以柯布道格拉斯生產函數（CD函數）為基礎模型進行適當變換，再結合數據構建回歸模型來進行定量計算的較多。從期刊發表論文看，學術界研究目前主要是熱衷于從第二個角度采用上述方法來測算不同省域或地區教育對經濟增長的貢獻率大小，較多關注于選擇不同地域并對其結果進行差距對比，而較少關注于選擇不同方法來對其結果進行差異比較。當然，不同方法基于不同理論框架，其測算出的結果的大小差距可比性可能較差，但是談及教育對經濟增長貢獻率測算問題，同樣數據采用不同方法和角度有時會得出截然不同甚至相差甚遠的結果和結論，到底哪種方法能更好地反映客觀實際？基于此，筆者嘗試采用兩種方法以估算江蘇省1991～2012年教育對經濟增長速度的貢獻率為例進行方法對比研究，以剖析不同方法及結果的差異性和優缺點。

1 方法及步驟介紹

1.1 基于CD生產函數的估算方法（簡稱方法1）

根據人力資本理論[1]，導致經濟增長的主要因素包括資本、技術及勞動，用柯布道格拉斯生產函數表示為考慮到教育因素對勞動力質量的作用，表達式又可以寫為。該模型也是目前實證研究較為流行的一種方法。公式中，t表示年份，Yt表示第t年總產出，At表示第t年技術進步率，Kt表示第t年物質資本，Lt表示勞動力人數，Et為教育投入。

第一步，用時間序列回歸法,將公式2兩邊取自然對數，求時間t全導數后，用差分方程近似代替微分方程為：y=a+αk+βl+βe+ε（公式3）。這里y表示年經濟增長率，a表示年技術進步率，α表示物質資本投入產出彈性，k表示資本投入年增長率，β表示勞動投入產出彈性，l表示勞動投入年增長率，e表示教育投入年增長率，ε為隨機誤差項。那么教育對經濟增長速度的貢獻可以表示為：Re=βe/y（公式4）。

第二步，將公式1兩邊取自然對數得到線性回歸模型:lnYt=lnAt+αlnKt+βlnLt，設α+β=1。為避免出現序列自相關和多重共線性問題，構造一階差分方程：lnYt-lnYt-1=C0+α(lnKt-lnKt-1)+β(lnLt-lnLt-1)+εt（公式5）。這里εt為隨機誤差項，假設其均值為0，且自變量一階差分與隨機誤差項無關。根據公式5并對相關基礎數據（見表1）作簡單處理后利用SPSS作回歸分析，得出相關系數R=0.891，R2=0.794，回歸估計標準誤差為0.0106，表明因變量與自變量之間高度相關，模型系數均通過檢驗（顯著性檢驗均在0.05以下），多重共線性檢驗為Tolerance=0.77，自變量之間不存在多重共線性，依此得到回歸模型為：lnYt=-0.02+0.903lnKt+2.078lnLt，將物質資本產出彈性а和勞動產出彈性β正規化處理后，а=0.303，β=0.697。

第三步，根據Re=βe/y（公式4）計算教育對經濟增長速度的貢獻。在實際計算中，e一般用起止年間教育綜合指數年平均增長率來表示教育投入年增長率，y為起止年間實際地區生產總值的增長率。教育綜合指數算法主要是采用明瑟收益率、勞動力簡化率等方法來表示不同受教育程度的勞動收入或勞動力生產率倍率從而反映教育投入的作用。本文采用被廣泛引用的Psacharopoulos提供的分教育階段教育回報率數據[2]，定教育回報率系數為小學教育階段0.18，中學教育階段0.134，高等教育階段0.151。設定勞動力人均受小學、初中、高中、大學及以上教育年限分別為6年、9年、12年、16年，則根據表1中各級文化程度人口百分比計算出起止年份人均受初等、中等、高等教育年限分別為P初（1991）=4.784、P中（1991）=1.566、P高（1991）=0.066；P初（2012）=5.689、P中（2012）=3.041、P高（2012）=0.514。則期始年份教育綜合指數 E1991=0.18*P初（1991）+0.134*P中（1991）+0.151*P高（1991）=1.081，同理算出期末年份教育綜合指數E2012=1.509,則e=[(E2012/E1991)1/21-1]*100%=1.601%。y=[(y2012/y1991)1/21-1]*100%=[(9928.89/683.6)1/21-1]*100%=13.59% ，Re=βe/y=0.697*0.01601/0.1359*100%=8.21%。

1.2 超越對數生產函數估算方法及步驟（簡稱方法2）

由Christensen（1973）創立的超越對數生產函數[3]表達式為[4]:lnYt=b0+b1t+b2lnLt+b3lnKt+b4t2+b5(lnLt)2+b6(lnKt)2+b7lnKtlnLt+b8tlnKt+b9tlnLt+μt（公式6）模型中，t為時間趨勢變量=T-1990，T為1991～2012年的時間序列。Yt表示第t年總產出，Kt表示第t年物質資本存量，Lt表示第t年教育要素投入的人力資本存量，μt為隨機誤差項。

第一步，為防止多重共線性問題，用公式6結合表1中相關數據作主成分回歸，提取了一個主成分，累計方差貢獻率達98.764%，特征值為λ=8.889，說明這1個主成分已經對大多數信息做出了充分概括，主成分提取結果比較理想。再對自變量主成分序列和因變量經Eviews協整關系檢驗，二者都是一階單整，說明不是偽回歸。經主成分分析、線性回歸、標準化系數還原等步驟最終得到關于原始變量模型為：

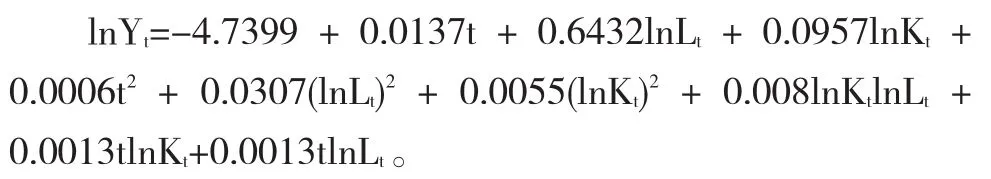
第二步，求出物質資本完全產出彈性（а）和人力資本完全產出彈性（β）分別為：а=(dY/Y)/(dK/K)=dlnY/dlnK=b3+2b6lnKt+b7lnLt+b8t=0.0957+0.011lnKt+0.0081lnLt+0.0013t；β=(dY/Y)/(dL/L)=dlnY/dlnL=b2+2b5lnLt+b7lnKt+b9t=0.6432+0.0614lnLt+0.0081lnKt+0.0013t。這里а和β是關于時間t的變彈性系數序列，方便起見，最后在表2中只列出各自起止年間平均完全產出彈性，分別為：

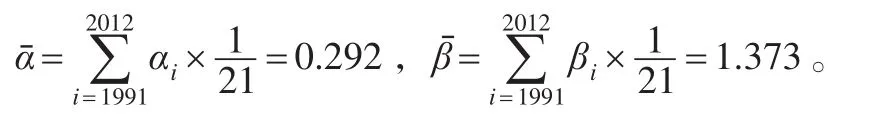
第三步，計算教育對經濟增長的貢獻率。物質資本存量和人力資本存量對經濟增長的完全貢獻率分別為GK和GL，表達式為：GK=а*(ΔK/K)/(ΔY/Y)*100%,GL=β*(ΔL/L)/(ΔY/Y)*100%。這里將人力資本存量看作是反映教育的投入作用，GL就是教育對經濟增長的貢獻率。由于а和β是數據序列，故求出的GK和GL也是關于時間t的數據序列，取完全貢獻率平均值為：。

2 數據說明及結果

2.1 數據說明

兩種模型所涉及基礎數據有：Y（實際GDP）、K(實際物質資本存量)、在業人口文化程度分布百分比、勞動力人數R和時間t。為了增加模型方法可比性，實證均采用相同數據，以《江蘇省統計年鑒》（2013年）、《中國統計年鑒》（1991～1995年）為來源，收集整理得到了模型中有關指標的基礎數據，見表1所示。

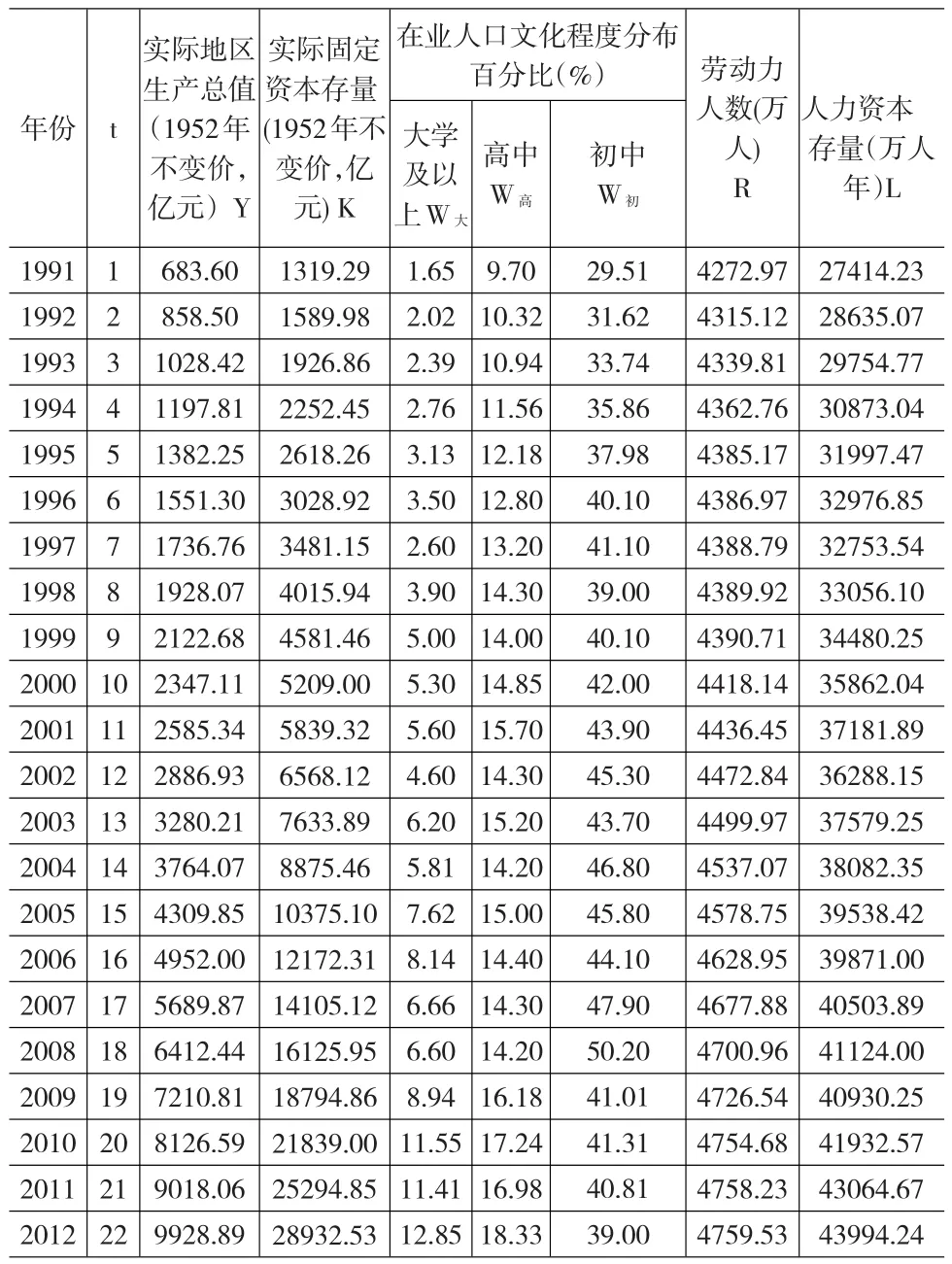
表1 江蘇省1991～2012年有關數據

數據說明：(1)“實際地區生產總值（1952年不變價，億元）”是根據“地區生產總值（當年價）、地區生產總值指數（可比價，上年=100）、地區生產總值指數(可比價，1952=100)”三項計算得出。(2)實際固定資本存量(1952年價格)”是用“固定資本形成總額（當年價）、固定資產投資價格指數（上年=1）、固定資產投資價格指數(1952=1)、經濟折舊率”數據依據張軍等(2004)[5]方法計算得出。(3)為了便于計算，這里將研究生、本科、專科教育全部合并歸類為大學及以上教育程度，不細分計算。

方法2中關于人力資本存量L算法有多種，如教育年限法、物質投入法、生產函數法、人力資本回報法等[6]。其中，教育年限法更便于操作，即直接使用勞動力教育水平反映人力資本。具體方法包括直接估計法和累積估計法，相比之下又以直接估計法最為常用,并且算出的數字就是絕對量[7]。考慮到數據可獲得性，本文采用教育年限法中的直接估計法，即用勞動力教育程度構成乘以相應勞動力人數來測算人力資本存量。勞動力人均受初等、中等、高等教育年限設定同方法1中第3步,各級文化程度人口百分比分別用W小、W初、W高、W大表示，Rt為第t年勞動力人數，則人力資本存量Lt=（W小*6+W初*9+W高*12+W大*16）*Rt，計算結果見表1所示。

2.2 計量結果

按照上述兩種方法步驟分別作數據分析，得到物質資本和人力資本產出彈性以及教育對經濟增長速度的貢獻率，計量結果見表2所示。

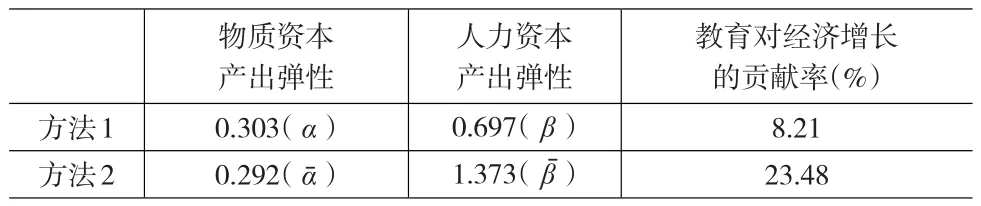
表2 兩種方法的計量結果

3 比較分析

兩種方法得到了截然不同的結果，且直觀來看差距較大，依此作如下一些比較分析：

（1）理論基礎。人力資本理論是眾多測算高等教育對經濟增長貢獻的主要理論基石，文中兩種方法也不例外。這兩種方法的共同點是把教育看成是影響勞動力質量的重要因素，通過教育可以使勞動力生產效率成倍增加。只是各自模型所隱含理論假設和角度略有不同。方法1生產函數模型是基于柯布道格拉斯生產函數，其理論假設是資本是同質并且得到充分利用，勞動力與資本按照邊際產品價格付酬，并且兩者之間可相互替代。所以，該模型揭示了經濟增長率是由勞動力數量增加、技術能力提高和資本投入決定的，是考察這些要素對經濟增長的直接貢獻。方法2生產函數模型除了體現經濟系統中人力資本和物質資本要素投入對經濟增長的直接貢獻外，還考慮到了這些要素相互影響以及各自隨著時間的動態改變，即人力資本溢出效應。因此方法2考察了人力資本對經濟增長的直接貢獻和間接貢獻，比方法1更加全面，更加符合客觀實際。

（2）模型構造。不同的理論前提，需要有不同的模型表達。在作回歸分析時，為了消除多重共線性問題，各自又采用了不同的解決方法。方法2模型中自變量較多共有9個，它們刻畫出了人力資本存量、物質資本存量以及時間這三者之間兩兩作用、自身影響的一種系統動態畫面。在作回歸分析時，為了避免自相關和多重共線性，采用了主成分分析法，將多個變量降維組合成一組新的互相無關的綜合變量來代替原始變量大部分信息。當然也有很多文獻在作超越對數生產函數模型分析時是采用嶺回歸來作降維處理。嶺回歸是通過放棄最小二乘法無偏性，以損失部分信息、降低精度為代價獲得回歸系數，是一種有偏估計，但它的精度卻能夠大大高于無偏估計量。方法1自變量較少，但因是時間序列，序列自相關和共線性顯然存在。它是采用一階差分方程形式來將原微分方程離散化，用差分方程代替微分方程重新構造變量，回歸時是基于最小二乘法的無偏估計。

（3）彈性系數。實證中，人力資本產出彈性系數β值的大小很大程度上決定了教育對經濟增長貢獻的大小。關于β系數，有些實證是用丹尼森的數字直接取0.8左右，這或許與中國具體國情有所不符，在數值上有些不合理。還有些研究是將β直接看待為教育對經濟增長貢獻率，這顯然是在概念上有所混淆。因為這里的β系數實際上只是反映了人力資本變量變化對經濟增長變量變化的敏感程度，只是勞動投入產出彈性，必須要轉化為教育投入產出的經濟價值形式變量才好與經濟增長變量比對，也才真正是教育對經濟增長貢獻所占份額。也有更多研究是采用實證數據構建回歸模型算出β系數，文中兩種方法都是將β看成是人力資本存量影響國民收入的解釋變量的回歸系數，由模型計量分析得出，看起來更加符合實際情況也更加科學。但是兩種方法算出的β系數性質各不相同，方法1的β系數是一種常替代彈性系數，是人力資本直接產出彈性，因此也決定了只能計算出教育對經濟增長的直接貢獻，但是計算結果較為直觀明了。當然也有學者認為用舒爾茨或是丹尼森等算法算出的教育對經濟增長貢獻仍然是教育的間接貢獻，原因是勞動力的價值形成源于教育但只在勞動過程中才得以體現，就教育來說，是間接所致[8]。方法2的β系數則是變替代彈性系數，是一組數值，相對復雜。但是它考慮到了勞動力、資本和技術等各種要素相互作用以及隨著時間推移的動態變化，它是既包括了直接產出彈性，也包括了間接產出彈性，即完全產出彈性，根據它能計算出教育對經濟增長的直接貢獻加間接貢獻即完全貢獻，但這種完全貢獻也只是相對的而非絕對意義上的完全貢獻，一定程度體現了勞動者從事社會活動持續影響著經濟增長的這部分。因此方法2的β系數能更加全面地反映實際情況。從表2可以看出，同樣的實證數據，方法2計算出的β值明顯比方法1大的多。

（4）貢獻率的差異。方法1是用教育綜合指數年增長率與勞動投入彈性來反映教育投入所帶來的這部分經濟收入增長對整個經濟增長的貢獻（Re=βe/y）。首先，在計算教育綜合指數時需要額外假定一套教育回報率或收益率數值（如明瑟收益率），這是脫離了模型本身的，有如“節外生枝”，會加大誤差。同時這些倍率數值通常是依據大量數據計算得到，但是由于計算年代較早和抽樣偏差目前也尚未形成統一數據，直接套用這些倍率數字來測算教育投入回報率顯然是不精準的。其次，這種用“從業人員不同人均受教育年限--不同收入回報率--教育綜合指數--教育投入回報”的簡單映射方式，顯然是較為片面和局限。因為在實際經濟社會現狀中，勞動者自身家庭背景、就業機遇、工作年限、工作經驗、勞動技能增長等因素都在不同程度地影響、決定著勞動生產效率和收入回報。勞動力生產水平和收入水平決不會因受教育年限的固定而一成不變。加之方法1中β系數為直接彈性，因此方法1計算出的貢獻率顯然會低估勞動對經濟增長的貢獻，使結果偏小。當然方法2中用直接教育年限法直接代替人力資本存量也是同樣存在著過于簡化的問題。但計算貢獻率時是完全基于模型自身算出，體現了模型的完整性和系統性。它涵蓋了教育對經濟增長的直接效應和溢出效應，是對經濟增長的完全貢獻率，表2中對比可見該方法結果大的多。因此用方法2算出的貢獻率結果顯得更加全面和合理。

4 討論

不同的方法基于不同的理論前提來架構模型從各自不同的角度闡釋著教育對經濟增長作用。結果本身的大小并沒有太大可比性，只有差異性。對比不同方法差異可以為該問題的研究、管理或決策提供更多視野和思路。文中采用相同實證數據，只是為了盡可能保證某些條件相同的情況下，更加清晰地對比和凸現不同實證模型所考察角度和結果迥異。考慮到數據可獲得性和目前學術研究偏好，只比較了教育對經濟增長速度貢獻率計量方法的差異，而沒有探討教育對經濟增長額貢獻率計量方法的差異，作為方法比較研究略顯不夠全面，也是不足。此外，對于該問題的實證研究，由于數據難于收集，依然存在著諸多困難，如：接受高等教育所帶來的精神生活收益提升以及對社會人文生活影響從而促進的經濟社會發展很難準確、定量衡量；在算教育回報率時，工資收入不光與受教育年限有關，還與家庭背景、機遇、工作種類也有關，目前單純地用收入倍率可能無法精準反映教育的作用等等。隨著方法不斷改進和創新，對該問題實證研究也將更加趨于科學和合理。

[1]Schultz.T W The Value of The Ability to Deal With Disequilibria[J].Journal of Economic Literature,1975,（13）.

[2]Psacharopoulos G,Patrinos A.Returns to Investment in Education:A Further Update[J].Education Economics,2004,12(2).

[3]Christensen L R,Jorgenson D W,Lau L J.Transcendental Logarithmic Production Frontiers[J].Review of Economics and Statistics.1973,（3）.

[4]吉彩紅,佟仁城,許健.基于超越對數生產函數的人力資本外溢效應研究[J].數學的實踐與認識，2009，（9）.

[5]張軍，吳桂英，張吉鵬.中國省際物質資本存量估算：1952～2000[J].經濟研究，2004,（10）.

[6]柏培文.全國及省際人力資本水平存量估算[J].廈門大學學報(哲學社會科學版),2012,（4）.

[7]柏培文.中國勞動力人力資本水平估算:1989～2007[J].教育與經濟,2010,（2）.

[8]胡慶十，吳怡興.關于教育投入外溢效益計量模型之我見——與周勝、劉正良商榷[J].教育與經濟,2013,（6）.