零售商部分延期支付下的動態庫存和融資策略

溫宗良，朱 雁，周優軍

（1.廣西中醫藥大學 藥學院，廣西 南寧 530001；2.徐州醫學院 公共教育學院，江蘇 徐州 221004；3.廣西科技師范學院 數學與計算機科學系，廣西 柳州 545004）

零售商部分延期支付下的動態庫存和融資策略

溫宗良1，朱 雁2，周優軍3

（1.廣西中醫藥大學 藥學院，廣西 南寧 530001；2.徐州醫學院 公共教育學院，江蘇 徐州 221004；3.廣西科技師范學院 數學與計算機科學系，廣西 柳州 545004）

在供應商允許零售商部分延期支付的條件下，討論了風險中性的零售商周期性地訂購一種產品以滿足不確定性需求的隨機動態庫存決策問題，建立了優化補貨和融資策略的庫存模型，目的是最大化零售商計劃期末的期望資金水平。零售商訂貨時可以使用自有資金和/或貸款資金，訂貨后如果有剩余資金，可通過無風險投資獲得無風險收益。分析了給定初始資金和庫存時的最優策略，并給出了數值實驗。

零售商；動態庫存；部分延期支付；訂貨策略；融資決策；隨機需求

1 引言

交易信用是指企業間在產品交易中以延期付款的方式進行購銷活動而形成的借貸關系，在實踐中得到了廣泛的應用。現實中的延期付款合同在執行時往往附帶一些支付條件，如供應商要求零售商收到訂貨時支付部分貨款[1]，如果提前期可以忽略不計，也就是要求訂貨時支付部分貨款。供應商為了降低違約風險，允許信用等級高的顧客（或老顧客）完全延期支付，而信用等級低的顧客（或新顧客）只能部分延期支付。在現實商業交易中，由于交易雙方財務狀況、合作程度、談判能力等的不同，這種供應商允許零售商在購買商品時只支付一定比例貨款而延期支付剩余貨款的交易行為廣泛存在。比如豐田公司要求他的供應商提供完全的交易信用，但只向其下游經銷商提供部分交易信用。

近年來，庫存決策中的資金問題備受重視，其中部分延期支付既能刺激下游零售商訂貨，又能在一定程度上減少其違約的風險，在現實中得到了廣泛使用，也引起了學者們的關注。Goyal[2]較早給出了存在延期付款時的EOQ模型，現有考慮部分延期和支付的文獻大都在Goyal[2]的基礎上放松某些假設進行推廣。Huang[1]在Goyal[2]的基礎上假定供應商允許零售商在訂貨量低于某一閾值時部分延期支付，建立了數學模型以確定最優訂貨周期和訂貨數量使得零售商的庫存費用最小。Ouyang等[3]以及賈濤等[4,5]將Goyal[2]的模型擴展到易腐品。Taleizadeh等[6]則研究了部分延期支付、缺貨部分補足的EOQ模型，分析了其最優訂貨量和缺貨量。Zhou和Zhong[7]在EOQ模型的基礎上，以零售商年平均費用最小為目標，建立了零售商在短信用期內可以部分付款并獲得價格折扣、在長信用期內支付剩余部分貨款的庫存模型，給出了求解過程。張義剛和唐小我[8]在報童模型的框架下，建立了允許零售商部分延期付款預期利潤模型，并用迭代算法確定了零售商不同保留利潤下制造商的最優決策。

現有考慮庫存和融資聯合決策的文獻大多研究單周期的問題，少有研究動態的多期問題。Archibald等[9]研究了最大化“自融資”初創企業長遠生存率的最優策略。Chao等[10]研究了最大化“自融資”企業期望計劃期末資產的最優策略。這兩篇文獻考慮利用內部資（和收入）的“自融資”，其他學者則考慮銀行貸款、債券、增發股票等多種外部融資。Babich和Sobel[11]在固定利率短期債務的條件下，以最大化IPO預期折現所得為目標研究企業的運營和財務決策。Xu和Birge[12]假設企業可通過借款和發行股票獲得資金，以最大化企業股東期望折現現金流為目標，立了有限計劃期上的庫存模型。Hu和Sobel[13]假設企業破產時支付違約懲罰后仍可運作，建立了與Xu和Birge[12]優化目標類似的模型研究企業的運營決策。Gong等[14]在Chao等[10]的基礎上假定企業每周期都可以使用自有資金和/或短期借貸資金，以企業期望計劃期末資產最大為目標，分析了企業的最優策略。

綜上，現有關于部分交易信用的文獻大多假設市場需求是確定的，在多周期部分延期支付條件下分析零售商的庫存和融資聯合決策的研究還未見發表。本文假設風險中性的零售商，在計劃期內周期性地從供應商處訂購一種產品以滿足不確定性需求，訂貨時需要支付一定比例的貨款，其余部分周期末支付，訂貨時可以使用自有資金和/或貸款資金，訂貨后如果有剩余資金，可以通過無風險投資獲得無風險收益，建立了以計劃期末的期望資金水平最大化為目標的隨機動態決策模型，在分析模型性質的基礎上，通過算例對模型進行了說明。

2 模型假設與記號說明

為了建立模型，引入如下記號與假設：

（1）將計劃期分為N個相等的訂貨周期；第n(1≤n≤N)個周期的需求為Dn，其概率密度函數和分布函數分別為φ(·)和?(·)，各周期的需求獨立且同分布；

（2）補貨率無限，提前期為零；允許缺貨，缺貨不補；本文的目標是最大化風險中性的零售商計劃期末的期望資金水平，信譽損失并不影響問題的結構和性質，不考慮信譽損失；

（3）bn,xn,yn分別為第n(1≤n≤N)個周期決策前的資金水平和決策前后的庫存水平，其中：-∞＜bn＜+∞, yn≥xn≥0;

（4）β為每次訂貨時立即支付貨款的比例，0＜β≤1；

（5）c,p,s分別表示單位產品購買價格、零售價格和計劃期末的殘值，h為每個周期單位剩余產品的庫存持有成本（不含資金成本），r,rf分別為每個周期內的貸款利率和無風險投資收益率，滿足：-∞＜s≤c＜p，c(1+βr)＜p;

（6）假設供應商資金充足，零售商有一定的資產且信用良好（如有債務，會如期償還）；

（7）a為實數，記a+=max{0,a}，a-=max{0,-a}。

3 模型建立

根據假設，零售商根據第n(1≤n≤N)期初的初始庫存水平xn和資金水平bn決定訂貨后的庫存水平為yn，即訂貨量為yn-xn，并立即支付β比例的貨款 βc(yn-xn)，剩余部分在本期末支付。零售商如果資金充足，滿足約束βc(yn-xn)≤bn，剩余資金將被進行無風險投資以獲得無風險收益如果資金不足以支付這部分貨款，零售商會通過向銀行融資完成訂單，并需在本期末償還本息零售商在期末實現本期需求Dn，可獲得收益需要支付庫存費用(第N期末可獲得殘值如果零售商期末現金不足以償還債務(包括延期支付的貨款和貸款本息)，零售商將再次融資，此時資金水平為負。

因此，零售商在第n(1≤n≤N)期末，即第n+1期初的庫存水平xn+1和資金水平bn+1分別為：

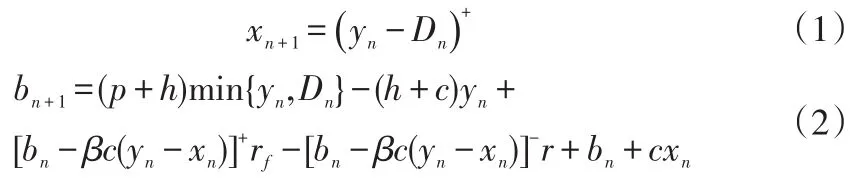
所以，零售商的決策問題是給定計劃期初的庫存水平x1和資金水平b1確定最優的訂貨策略，使計劃期末的期望現金流最大，決策的優化問題為且需滿足（1）、（2）兩式及yn≥xn≥0。

記Vn(x,b)(1≤n≤N)為給定初始庫存水平x和資金水平b的計劃期末期望現金最大值，則最優性方程為：

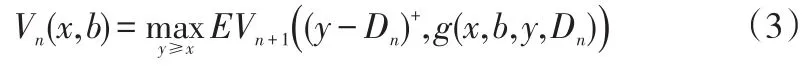
其中，

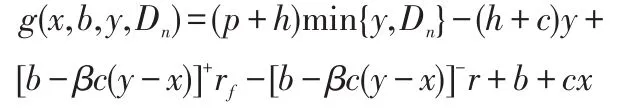
邊界條件為：VN+1(x,b)=b+sx。

當β=1時，我們的模型即為Gong等[14]所構建的模型。

4 模型分析與求解

為了得到最優的訂貨策略，有：

引理1 對任意第n周期，固定x，則Vn(x,b)關于b遞增。

引理1是很直觀的：零售商期初的資金越多，計劃期末的期望現金越多。

引理2 對于任意第n周期,固定A和B,則Vn(A-z,B+(p+h)z)關于z遞增。

證明：對于任意第n周期，固定A和B，由式（3），得：

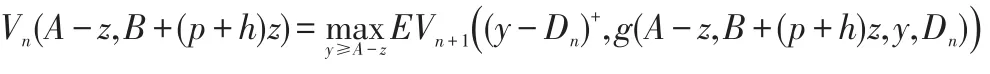
引理2表明在每周期初持有現金比庫存更有利。因為通過訂貨可將現金轉化為庫存，反之不行，所以期初持有現金比庫存更靈活。而持有庫存太多且超過必需水平時，會失掉持有現金而獲得無風險收益的機會。

定理1 對于任意第n周期，Vn(x,b)是關于(x,b)的凹函數。

證明：使用歸納法進行逆推。

顯然，VN+1(x,b)=b+sx是關于 (x,b)的凹函數。假設Vn+1(x,b)是關于(x,b)的凹函數，下面證明Vn(x,b)是關于(x,b)的凹函數。

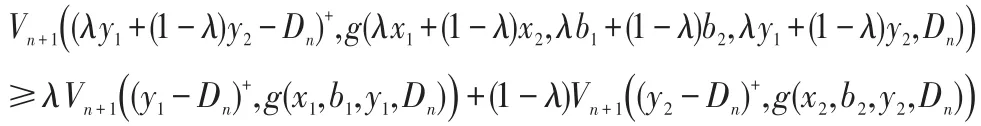
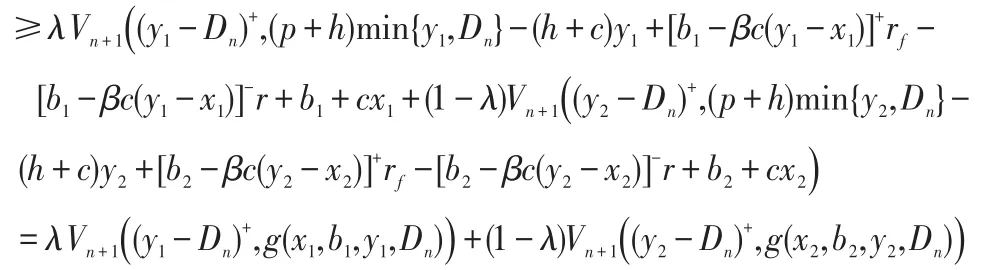
記R=x+b/(βc)表示零售商用盡自有資金但不貸款所能達到的訂貨后的庫存水平，稱之為“自有庫存資產”。

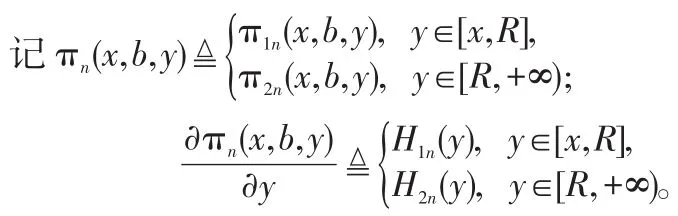
類似定理1的證明可得,對任意第n周期，給定(x,b), πn(x,b,y),π1n(x,b,y)和 π2n(x,b,y)都為關于 y的凹函數，且H1n(R)≥H2n(R)。記π1n(y),π2n(y)和πn(y)分別為給定(x,b)時π1n(x,b,y),π2n(x,b,y)和πn(x,b,y)的函數值。由πn(y)的連續性可知，π1n(R)=π2n(R)。記H1n(y)=0，H2n(y)=0的根分別為 y1n和y2n，由πn(y)的連續性及π1n(y)和π2n(y)的凹性，有：

引理3 若y1n＜R，則y2n＜R。

證明 反證法。假設y2n≥R則H2n(R)≥0。由y1n＜R知H1n(R)＜0，從而H2n(R)＞H1n(R)。這與H1n(R)≥H2n(R)矛盾。因此，若y1n＜R，則y2n＜R。證畢。

定理2 當第n期初狀態為(x,b)且b＞0時，零售商的最優訂貨策略如下：

（1）若y1n≤x，則不訂貨；

（2）若x＜y1n≤R，則訂至y1n;

（3）若y2n＜R≤y1n，則訂至R;

（4）若R≤y1n且R≤y2n，則訂至y2n。

證明 根據x與y1n,y2n的大小關系，分以下四種情形討論：

情形1：y1n≤x且y2n≤x。

由y1n≤x知π1n(y)在區間[x,R]上單調遞減，則對任意的y∈(x,R)，有π1n(R)≤π1n(y)＜π1n(x)，又由y2n≤x知π2n(y)在區間(R,+∞)上單調遞減，則對任意的y∈(R,+∞)，有π2n(y)＜π2n(R)，而π1n(R)=π2n(R)，可得yˉ=x。

情形2：y1n＜x且y2n＞x。

由y1n＜x得y1n＜R及引理2知y2n＜R，此時π2n(y)在區間(R,+∞)上單調遞減，則對任意的y∈(R,+∞)，π2n(y)＜π2n(R)。

由y1n＜x知π1n(y)在區間[x,R]上單調遞減，則對任意的y∈(x,R]，有 π1n(R)≤π1n(y)＜π1n(x)，再由 π1n(R)=π2n(R)，得yˉ=x。

情形3：y1n＞x且y2n＜x。

顯然有y2n＜R，從而π2n(y)在區間(R,+∞)上單調遞減，則對任意的y∈(R,+∞)，π2n(y)＜π2n(R)。

當x＜y1n＜R時，由π1n(y)的凹性，知對任意的y∈[x,R]，π1n(y)≤π1n(y1n)，再由π1n(R)=π2n(R)，得yˉ=y1n。

當y1n≥R時，π1n(y)在區間[x,R]上單調遞增，則對任意的y∈[x,R)，π1n(y)＜π1n(R)，再由π1n(R)=π2n(R)，得yˉ=R。

情形4：y1n＞x且y2n＞x。

當 x＜y1n＜R時，由引理2知 y2n＜R，此時π2n(y)在區間(R,+∞)上 單 調 遞 減 ，則 對 任 意 的 y∈(R,+∞)，有π2n(y)＜π2n(R)。由 π1n(y)的凹性，知對任意的 y∈[x,R]，有π1n(y)≤π1n(y1n)，再由π1n(R)=π2n(R)，得yˉ=y1n。

當 y1n≥R 時，分 y2n＜R 和 y2n≥R 進行討論。當y1n≥R＞y2n時，π1n(y)在區間[x,R]上單調遞增，π2n(y)在區間(R,+∞)上單調遞減，則對任意的y∈[x,R)，有π1n(y)＜π1n(R)，對任意的 y∈(R,+∞)，有 π2n(y)＜π2n(R)，由 π1n(R)=π2n(R)，得yˉ=R。當 y1n≥R且 y2n≥R時，π1n(y)在區間[x,R]上單調遞增，則對任意的y∈[x,R)，有π1n(y)＜π1n(R)，又由π2n(y)的凹性，知 對 任 意 的 y∈[R,+∞)，有 π2n(y)≤π2n(y2n)，再 由π1n(R)=π2n(R)，得yˉ=y2n。

綜上可知，若y1n≤x，則不訂貨；若x＜y1n＜R，則訂至y1n；若y2n＜R≤y1n，則訂至R；若R≤y1n且R≤y2n，則訂至y2n，證畢。

定理3：當第n個周期期初狀態為(x,b)且b≤0時，零售商的最優訂貨策略為：若y2n≤x，則不訂貨；否則，訂到y2n。

從定理2可以看出，當第n期初資金水平為正時，庫存系統存在兩個訂貨的臨界值y1n和y2n。當期初庫存水平高于或等于臨界值y1n時，最優策略為不訂貨，自有資金全部存入賬戶獲得無風險利息，否則，最優策略取決于兩個臨界值和“自有庫存資產”的大小關系。如果“自有庫存資產”大于臨界值y1n，則最優策略為訂貨到y1n，此種情形訂貨后仍有資金剩余，剩余資金存入賬戶獲得無風險利息；如果“自有庫存資產”介于兩臨界值之間，則最優策略為用盡自有資金，此時沒有剩余資金，也無需融資；如果“自有庫存資產”不超過兩臨界值，則最優策略為訂貨到y2n，此時自有資金不足以使訂貨達到y2n，零售商需要通過融資來完成訂貨。

從定理3可以看出，當第n期初資金水平為非正時，庫存系統的訂貨策略相對簡單，只有一個訂貨的臨界值y2n，此時庫存策略只依賴于期初庫存水平和此臨界值的大小關系。當期初庫存水平高于或等于臨界值y2n時，最優策略為不訂貨；否則最優策略為訂貨到y2n，此時，零售商需要通過融資來完成訂貨。

5 數值實驗

設計劃期分為4個訂貨周期，零售商每周期初的采購價格c=2，零售價格p=2.5，計劃期末的殘值s=1，訂貨時立即支付貨款的比例β=0.85，每周期單位剩余產品的庫存持有成本h=0.1，每個周期內的貸款利率和無風險利率分別為r=0.2和rf=0.05。每個周期的需求都為獨立同分布的截尾正態分布，均值和標準差分別為4和1.5。表1列出了零售商各周期（部分）給定初始狀態的最優訂貨策略。表中第二行表示每周期初的庫存水平，第一列表示每周期初的資金水平，表格中數據為行列交叉所表示狀態的最優訂貨策略（訂貨后達到的庫存水平）。3.03。由表1可以看出，對于第4周期策略結構比較簡單，存在兩個臨界值，給定期初狀態的最優策略取決于狀態與臨界值的關系；而對于其他各周期（此處以第3周期為例），由于模型本身的復雜性導致策略結構比較復雜，存在著某些區域，當給定初始庫存（資金）而擁有更多的資金（庫存）時，訂貨后達到的庫存水平反而會減少，這與第4周期所具有的給定初始庫存（資金）時資金（庫存）增加則訂貨后達到的庫存水平不減這一性質不同，文獻[14]中的模型也有類似的性質。這種反直觀的現象來源于多余資金的投資價值。

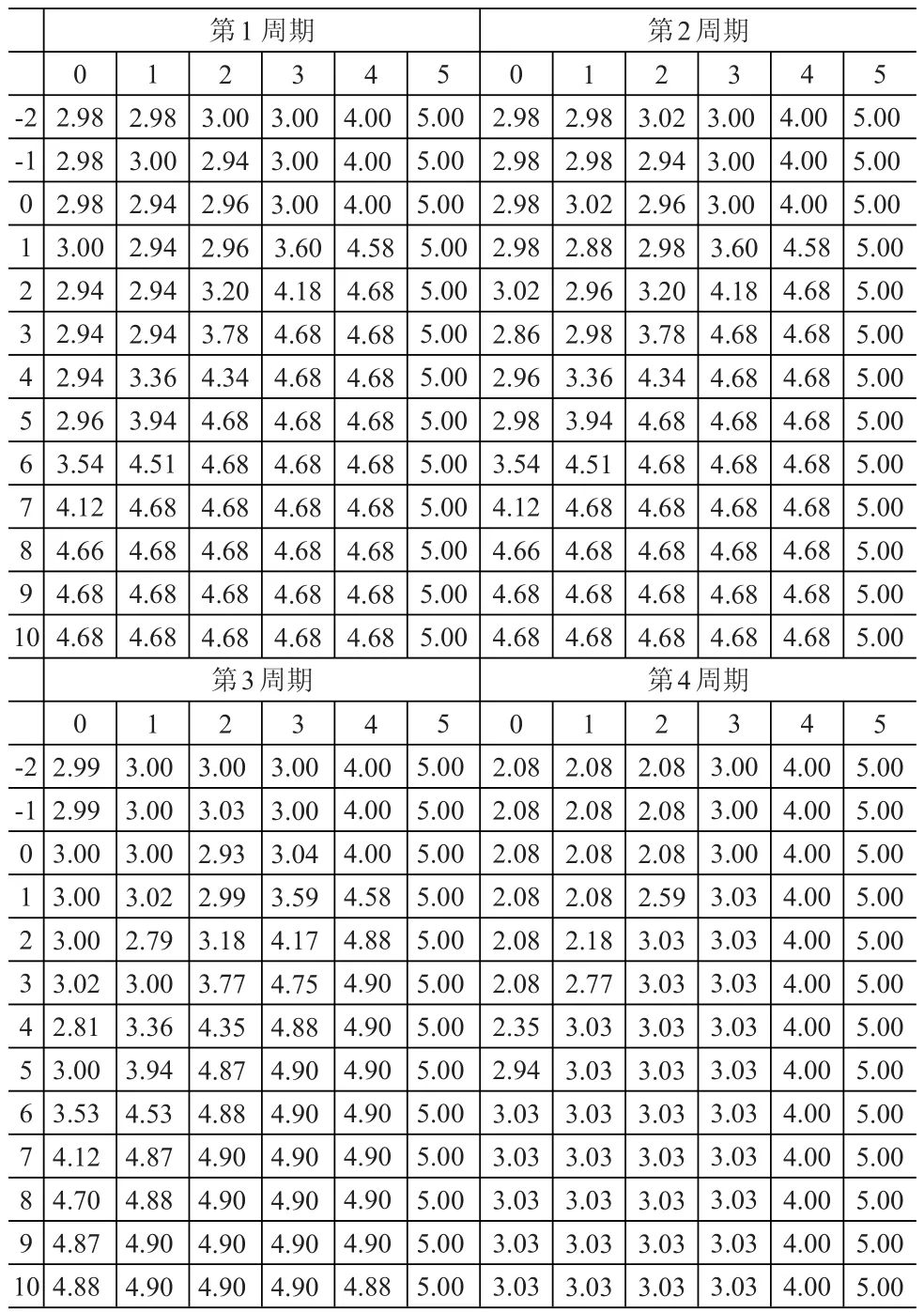
表1 零售商各周期給出初始狀態的最優訂貨策略

6 結論

在現實中，由于交易雙方財務狀況、合作程度、談判能力等的不同，部分延期支付廣泛存在于交易實踐中。本文從實際出發，假設風險中性的零售商存在資金約束，在供應商允許部分延期支付的條件下周期性地訂購一種產品以滿足不確定性需求，訂貨時可以使用自有資金和（或）貸款資金，訂貨后如果有剩余資金，可以通過無風險投資獲得無風險收益，以最大化計劃期末的期望資金水平為目標，建立了隨機動態模型。在分析模型性質的基礎上，通過算例對模型進行了說明。本文的研究對于市場需求不確定下實施部分信用交易的訂貨和融資聯合決策具有一定的理論價值。進一步的研究方向，可以考慮零售商的風險偏好、存在破產風險等情形。

[1]Huang Y F.Economic order quantity under conditionally permissible delay in payments[J].European Journal of Operational Research,2007, 176(2):911-924.

[2]Goyal S K.Economic order quantity under conditions of permissible delay in payments[J].Journal of the Operational Research Society,1985, 36:335-338.

[3]Ouyang L Y,Teng J T,Goyal S K,et al.An economic order quantity model for deteriorating items with partially permissible delay in payments linked to order quantity[J].European Journal of Operational Research,2009,194(2):418-431.

[4]賈濤,徐渝,耿凱平.部分延期付款下易腐品聯合經濟訂貨批量模型究[J].運籌與管理,2011,20(8):1-9.

[5]賈濤,鄭毅,徐渝,等.顧客部分延期付款下兩級商業信用易腐品訂貨策略[J].運籌與管理,2013,22(2):150-158.

[6]Taleizadeh A A,David W P,Mohammad S J,et al.An EOQ model with partial delayed payment and partial backordering[J].Omega,2013,41(2): 354-368.

[7]Zhou Y W,Zhong Y G.How to make the replenishment and payment strategy under flexible two-part trade credit[J].Computers&Operations Research,2013,40(5):1 328-1 338.

[8]張義剛,唐小我.部分延期付款下的制造商決策與供應鏈協調[J].管理學報,2012,9(10):1 536-1 547.

[9]Archibald T,Thomas L,Betts J,et al.Should start-up companies be cautious?Inventory policies which maximize survival probabilities[J].Management Science,2002,48(9):1 161-1 174.

[10]Chao X,Chen J,Wang S.Dynamic inventory management with cash flow constraints[J].Naval Research Logistics,2008,55(8):758-768.

[11]Babich V,Sobel M J.Pre-IPO operational and financial decisions[J]. Management Science,2004,50(7):935-948.

[12]Xu X,Birge J R.Equity valuation,production,and financial planning: A stochastic programming approach[J].Naval Research Logistics,2006, 53(7):641-655.

[13]Hu Q,Sobel M J.Echelon base-stock policies are financially sub-optimal[J].Operations Research Letters,2007,35(5):561-566.

[14]Gong X,Chao X,Simmchi D.Dynamic inventory control with limited capital and short-term financing[J].Naval Research Logistics,2014,61 (3):184-201.

[15]Heyman D P,Sobel M J.Stochastic models in operations research:stochastic optimizations[M].Courier Dover Publications,2003.

Study on Dynamic Inventory and Financing Strategy with Partial Delay in Payment by Retailer Allowed

Wen Zongliang1,Zhu Yan2,Zhou Youjun3
(1.School of Pharmacy,Guangxi University of Chinese Medicine,Nanning 530001; 2.School of Public Education,Xuzhou Medical College,Xuzhou 221004; 3.School of Mathematics&Computer Science,Guangxi Normal College of Science&Technology,Liuzhou 545004,China)

In this paper,upon the premise that the supplier allows the partial delay in payment of the retailer,we discussed the stochastic dynamic inventory decision-making problem of a risk-neutral retailer that made cyclic ordering of a product to meet the uncertain demand for it,built the inventory model that optimized its replenishment and financing strategies so as to maximize the expected fund level of the retailer at the end of a term,and at the end,presented a numerical example to analyze the optimal initial investment and the optimal inventory level.

retailer;dynamic inventory;partial delay in payment;ordering strategy;financing decision-making;stochastic demand

F715.6；O141.4

A

1005-152X(2015)11-0067-05

10.3969/j.issn.1005-152X.2015.11.020

2015-10-02

國家自然科學基金項目（71261002）；廣西高校科學技術研究項目（KY2015YB366）；廣西中醫藥大學項目（QN14006）

溫宗良（1981-），男，山東聊城人，博士研究生，講師，研究方向：庫存控制、供應鏈金融；朱雁（1983-），女，安徽蕭縣人，講師，研究方向：優化與管理；周優軍(1974-)，通訊作者，男，廣西全州人，碩士，副教授，研究方向:物流與供應鏈管理。