復合材料加筋壁板低速沖擊響應與沖擊能量關系

石曉朋，李曙林，常 飛，卞棟梁，尹俊杰

(空軍工程大學 航空航天工程學院，西安 710038)

?

復合材料加筋壁板低速沖擊響應與沖擊能量關系

石曉朋，李曙林，常 飛，卞棟梁，尹俊杰

(空軍工程大學 航空航天工程學院，西安 710038)

基于ABAQUS有限元軟件，采用Hashin損傷準則建立了一種有效的復合材料加筋壁板低速沖擊模型。分析了接觸力、加筋壁板吸收能量和損傷散逸能對沖擊響應的影響。結果表明：隨著沖擊能量的增大，接觸力峰值前移，且沖擊后板吸收能量與損傷散逸能的差值變大。落錘沖擊實驗表明，低速沖擊能量下損傷程度與沖擊能量正相關。對比了損傷區域的仿真結果和實驗結果，發現二者擬合較好。

復合材料加筋壁板；沖擊響應；有限元分析；損傷面積；沖擊能量

復合材料加筋壁板結構是由加強筋(筋條)和被支撐的殼體(蒙皮)組成的結構，其不僅具有已有復合材料層合板結構比強度高、比剛度高以及結構可設計性好等特點，而且還具有自身所固有的諸多優點，例如自動化的低成本制造過程和高可靠性等[1]，因而，越來越多地應用于航空航天領域和各種工程結構中。然而，復合材料加筋壁板同復合材料層合板一樣，對沖擊載荷十分敏感，在低速沖擊載荷作用下，會出現基體開裂、分層、纖維斷裂等損傷，這種損傷范圍較大且不易發現，往往會給材料帶來更大威脅。因此，對加筋壁板在低速沖擊載荷作用下響應的研究具有重要意義。

目前，國內外許多學者針對復合材料層合板低速沖擊損傷機理進行了研究。Davies等[2]用較低能量進行沖擊，發現接觸力與時間關系曲線近似為正弦曲線，揭示了層壓板損傷面積與沖擊能量、最大接觸力的關系； Schoeppner等[3]總結出了分層門檻力與其他參數的相關關系；Feraboli等[4-6]證實，當沖擊能量較低、且在彈性沖擊階段時，損傷萌生接觸力、峰值接觸力與能量成正比關系，當能量增大到能夠產生損傷時，損傷會耗散能量，接觸力不再增加，出現一個平臺，甚至損傷一開始便出現平臺，沒有線性上升。

復合材料沖擊損傷機理較為復雜，目前暫無精確解析解。有限元的分析作為一種高效和低成本的分析方法，能較好預測沖擊響應及損傷。Lopes等[7]使用ABAQUS對沖擊過程進行有限元模擬，對實驗方法和數值方法的沖擊力曲線以及有限元預測的損傷面積與實驗的分層面積進行了比較，對能量的損傷耗散作了討論；Wang等[8]根據Hashin準則，及損傷演化規律，實現材料隨損傷出現剛度矩陣的折減；王一飛等[9]研究不同鋪層層合板低速沖擊響應與損傷參數之間的關系；王仁鵬等[10]基于Hashin失效準則，通過引入損傷變量對材料的彈性參數進行折減，研究了層壓板在靜痕作用下的損傷阻抗。古興瑾等[11]對復合材料加筋壁板高速沖擊損傷進行了數值模擬，并探討了筋條參數對高速沖擊損傷的影響規律。嚴實等[12]運用AE參數很好地描述了不同編織工藝參數三維編織復合材料的低速沖擊過程。

本工作結合有限元仿真方法，對復合材料加筋壁板在低速沖擊載荷作用下的接觸力、損傷散逸能和板吸收的能量等沖擊響應與沖擊能量關系進行了研究，并對比了仿真與實驗得到的損傷擴展結果。

1 低速沖擊損傷理論分析

1.1 沖擊分析模型及接觸力計算

最大的接觸力及位移是利用能量平衡方程得到，基本假設是最大接觸力或最大位移時刻所有沖擊能量都變換到板中，能量損失及材料阻尼及振動略去，即

(1)

式中：M，V分別為沖擊物的質量及速度；δ，α分別表示板上沖擊點處的撓度及接觸時的刻痕(凹坑)深度；F為接觸力。方程中右邊第一項為板彎曲變形能，第二項為接觸表面的接觸能量。

(2)

式中：k為板接觸點處的剛度。顯然，它是板尺寸大小、邊界條件、層壓板材料、板形狀等的參數。用有限元分析計算時都需考慮到這些因素。

根據Hertz接觸定

(3)

式中：n為Hertz接觸剛度，近似用式(4)，(5)求得。

(4)

或

(5)

式中：Ez為板垂直板面方向的彈性模量；rα為刻痕半徑；Es，νs為沖頭的彈性模量及泊松比；νz為層合板的泊松比(可取ν12)。將式(2)和式(3)帶入式(1)積分計算后得

(6)

1.2 失效準則

Hashin失效準則可以較好地應用于復合材料的損傷破壞分析中，本工作采用Hashin失效準則[14]作為失效判據，表達式如下纖維斷裂

(7)

纖維屈曲

(8)

基體壓縮失效

(9)

基體拉伸失效

(10)

拉伸分層失效

(11)

剪切分層失效

(11)

式中：1為纖維方向；2為纖維橫向方向；3為厚度方向；σ為對應方向的應力；S是對應方向的剪切強度；Xt是纖維方向的拉伸強度；Yt是橫向拉伸強度；Xc是縱向壓縮強度；Yc是橫向壓縮強度；ef，em，ed分別為纖維失效因子，基體失效因子，分層失效因子，當ei≥1(i=f，m，d)時，材料失效。

1.3 剛度退化方案

目前，針對復合材料損傷的剛度退化方案大致分為應力更新剛度退化方案，參數折減剛度退化方案和漸進損傷剛度退化方案。復合材料損傷過程中，損傷區域的應力分布變化很劇烈，漸進損傷剛度退化方案能較好地表征材料損傷形式和程度[17]，因此，其更適合用作復合材料損傷演化的判據[18]。

在沖擊過程中，當滿足Hashin失效準則時，材料開始失效，剛度矩陣開始退化。纖維損傷參數df和基體損傷參數dm分別表示

(12)

式中Lc為材料積分點處的特征長度;Gm為剪切模量。

在漸進損傷過程中，剛度矩陣根據纖維損傷參數df和基體損傷參數dm進行衰減，剛度退化方案為

(13)

1.4 黏滯規律

模型中加入了剛度退化方案，但是由于剛度的大幅度折減易引起計算收斂難，在顯式分析中往往表現為大變形下單元的過度扭曲而導致分析進程的中止，為了提高收斂度，本工作引入基于黏滯規律的技術[16]，黏滯變量為

(14)

式中:η為黏滯系數；d為計算得到的纖維損傷參數或基體損傷參數；dv黏滯變量。黏滯系數的選擇取決于對結果精度的要求，當黏滯系數選取較大時，其會明顯延緩材料的剛度折減進程。為了在t0+Δt時刻更新損傷變量，定義t0+Δt時刻損傷變量為

(15)

2 仿真模型及實驗

2.1 落錘沖擊實驗

采用直徑為16mm的沖頭進行落錘沖擊實驗，沖擊點為實驗件的中央處，如圖1所示。沖擊完成后，測量沖擊點處的凹坑深度，并使用超聲C掃描測量損

圖1 沖擊位置Fig.1 The position of impact

傷面積和損傷直徑。

2.2 仿真模型

對復合材料加筋壁板進行建模。本模型將實驗件分為兩個部分：蒙皮和筋條。蒙皮采用連續殼單元SC8R，筋條采用實體單元C3D8R，兩者用Cohesive(COH3D8)單元連接。蒙皮與筋條的厚度與鋪層方式一致，厚度為2.75mm，鋪層為[(45/-45/0/90/0)4/45/-45]，層合板的單層厚度為0.125mm，共22層。對于ABAQUS軟件，由于Hashin準則只能應用于殼單元，因此，對于筋條部分的損傷需要編寫子程序(VUMAT)。實驗件示意圖如圖2所示。

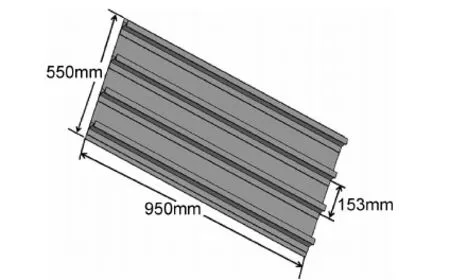
圖2 實驗件示意圖Fig.2 The sketch of test piece

沖頭設為剛體，沖擊點處進行網格細化。沖擊能量分別選取10，15，20，25J。邊界條件為蒙皮四邊固支，復合材料加筋壁板的材料屬性如表1所示。

表1 復合材料加筋壁板的材料屬性

3 結果與分析

3.1 損傷區域的有限元仿真與實驗結果對比

本工作建立的仿真模型模擬了沖擊過程中損傷的擴展情況，并計算了損傷區域的面積，如圖3所示，紅色區域ei≥1，即損傷區域，并與實驗得到的無損檢測C掃描圖進行對比。由于沖擊能量為10J的仿真結果與實驗結果均沒有出現損傷區域，因此將沖擊能量為15，20，25J三個能量水平的損傷區域進行了對比。

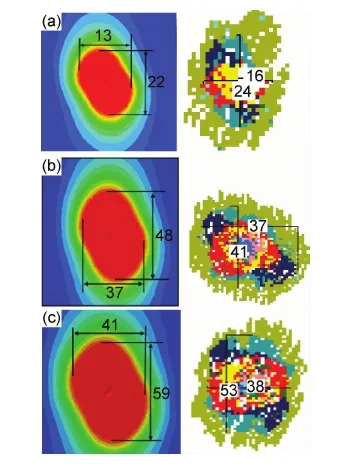
圖3 損傷區域圖 (a)15J;(b)20J;(c)25JFig.3 The drawing of damage area (a)15J;(b)20J;(c)25J

由圖3可以看出，由于復合材料結構各向異性，沖擊損傷區域呈現出類似橢圓形狀。且仿真得到的損傷區域與實驗C掃描得到的損傷區域形狀大致相同，損傷區域的最長和最寬處的比較接近。仿真與實驗得出的損傷區域面積結果如表2所示。

表2 仿真與實驗損傷區域面積對比

可以看出，模型計算得到的結果與實驗結果相近，兩者之間誤差較小，說明建立的模型合理且有效。

3.2 沖擊過程中的力學響應

通過有限元計算得到不同沖擊能量下接觸力、復合材料加筋壁板吸收能量及損傷散逸能隨時間的變化曲線，如圖4所示。

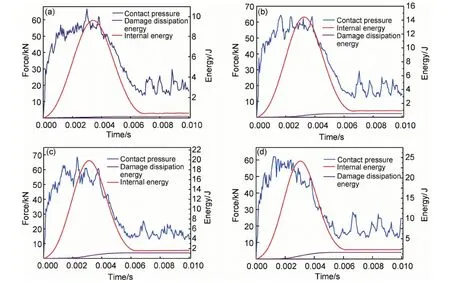
圖4 沖擊過程力學響應曲線 (a)10J;(b)15J;(c)20J;(d)25JFig.4 Dynamics response curves in impact process (a)10J;(b)15J;(c)20J;(d)25J

在沖擊過程的初始階段，接觸力隨時間成線性增長，由于加入漸進損傷剛度退化方案，剛度矩陣出現衰減，接觸力出現小幅振蕩。當達到損傷判斷準則時，復合材料加筋壁板開始出現損傷，剛度矩陣進一步衰減，接觸力開始大幅度振蕩。當能量增大到能夠產生損傷時，損傷會耗散能量，接觸力不再增加，出現一個平臺，甚至損傷一開始便出現平臺，沒有線性上升。當沖擊速度為0時，板吸收的能量達到最大值，但由于板的振蕩波的存在，接觸力在衰退的過程中仍然存在振蕩。

對于能量的變化情況，隨著沖頭與板接觸時間的增加，沖擊能量逐漸轉化為加筋壁板的內能，而當沖頭的速度為0時，沖擊能量為0，此時沖擊能量絕大部分轉化為加筋壁板的內能(少部分由于摩擦存在而轉化為其他的能量)。此后，加筋壁板的內能隨板的彈性變形和板的振蕩動能而逐漸消失，但并沒有完全消失。因為由于沖擊載荷的作用，加筋壁板出現損傷散逸能，此部分能量隨著損傷的出現而永久成為加筋壁板內能的一部分。

對于不同沖擊能量，接觸力、板的內能及損傷散逸能的變化曲線有所不同。由圖4可以看出，沖擊能量越大，在沖擊速度為0時，板吸收的內能越大。不同沖擊能量下，接觸力峰值出現的時間也有所不同，對于10J沖擊能量，接觸力峰值與板內能最大值出現時間一致，而對于15，20J及25J的沖擊能量，隨著沖擊能量的增大，接觸力峰值較板內能出現時間變早，認為這是由于不同沖擊能量對板的損傷程度有所不同，對于10J沖擊能量，板幾乎沒有出現損傷，結構主要為彈性變形。由胡克定律可知，沖擊速度為0時，板的變形最大，因此接觸力也最大；而對于結構出現損傷的情況，剛度矩陣衰減，此時接觸力峰值與變形量不成正比關系。對于25J沖擊能量，損傷范圍較大，剛度矩陣衰減嚴重，接觸力峰值較板內能峰值出現早。本文認為，加筋壁板吸收的能量并不完全為損傷散逸能，還有部分用于產生板的永久變形(復合材料的“塑性變形”)。這體現在當沖擊過程結束后，板的內能與損傷散逸能并沒有完全重合。而不同沖擊能量下兩者之間的差值不同，沖擊能量越大，兩者之間的差值越大，具體如表3所示。

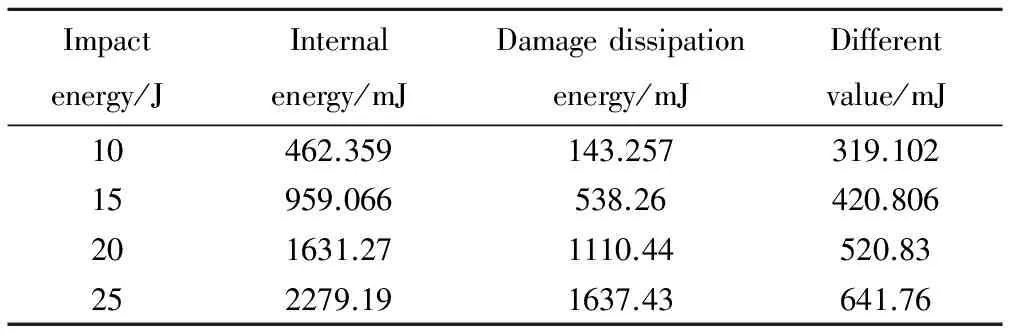
表3 吸收內能與損傷散逸能差值

沖擊過程中全部的沖擊能量分配如圖5所示。

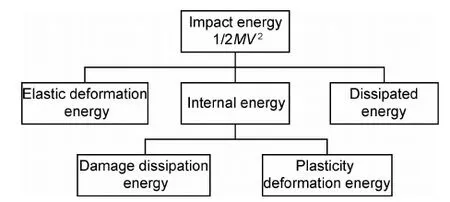
圖5 沖擊能量分配圖Fig.5 Distribution map of impact energy

3.3 凹坑深度與損傷面積隨沖擊能量變化

落錘沖擊實驗后，進行了凹坑深度測量和C掃描無損檢測，得到了不同沖擊能量下凹坑深度和損傷面積與沖擊能量的關系，如圖6，7所示。凹坑深度和損傷面積的大小取決于沖擊能量的大小，對于低速未穿透性損傷，兩者之間基本呈線性關系，即沖擊能量越大，凹坑深度越深，損傷面積越大。

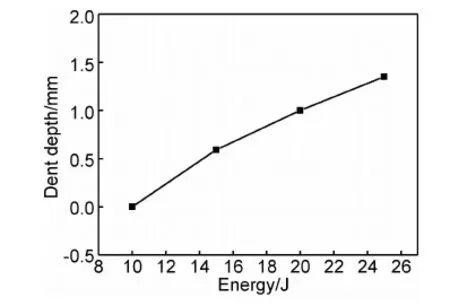
圖6 凹坑深度與沖擊能量關系Fig.6 Dent depth versus impact energy

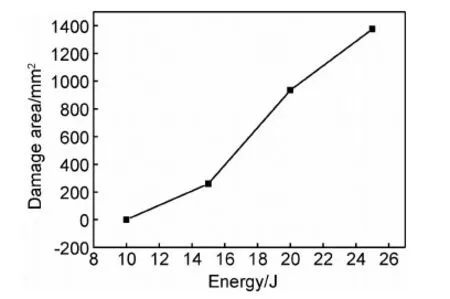
圖7 損傷面積與沖擊能量的關系Fig.7 Damage area versus impact energy

4 結論

(1)建立的仿真模型有效地模擬了低速沖擊過程中加筋壁板損傷擴展情況，所得損傷區域與實驗C掃描結果吻合較好，不同沖擊能量下仿真結果與實驗結果誤差在13%左右。

(2)接觸力在沖擊開始階段成線性增加，當加筋壁板出現損傷時，剛度矩陣衰減，接觸力曲線發生振蕩；隨著沖擊能量的增加，接觸力峰值出現時間前移，并且板吸收的內能與損傷散逸能之間的差值變大。

(3)在低速未穿透沖擊能量下，隨著能量增大，凹坑深度與損傷面積具有較好的正相關關系。

[1] 中國航空研究院.復合材料結構設計手冊[M].北京：航空工業出版社，2001.

China Aviation Academy. Composite Material Structure Design Manual[M]. Beijing:Aviation Industry Press,2001.

[2] DAVIES G A O, ZHANG X. Impact damage prediction in carbon composite structures[J]. International Journal of Impact,1995,16(1):149-170.

[3] SCHOEPPNER G A, ABRATE S. Delamination threshold loads for low velocity impact on composite laminates[J]. Composites Part A:Applied Science and Manufacturing,2000,31(9):903-915.

[4] FERABOLI P J, KEDWARD K T. A new composite structure impact performance assessment program[J]. Composites Science and Technology,2006,66(10):1336-1347.

[5] FERABOLI P J, KEDWARD K T. Enhanced evaluation of the low-velocity impact response of composite plates[J]. AIAA Journal,2004,42(10):2143-2152.

[6] FERABOLI P J. Some recommendations for characterization of composite panels by means of drop tower impact testing[J]. Journal of Aircraft,2006,43(6):1710-1718.

[7] LOPES C S, CAMANHO P P, GURDAL Z, et al. Low-velocity impact damage on dispersed stacking sequence laminates.part II:numerical simulations[J]. Composite Science and Technology, 2009,69(8):937-947.

[8] WANG Y Q, TONG M B, ZHU S H. Three dimensional continuum damage mechanics model of progressive failure analysis in fibre-reinforced composite laminates[A]. AIAA/ASME/ASCE/ AHS/ASC Structures,Structural Dynamics,and Materials Conference[C]. California:Palm Springs,2009.

[9] 王一飛，張曉晶，汪海.復合材料層壓板低速沖擊響應與損傷參數關系研究[J].固體力學學報，2013，34(1)：63-72.

WANG Yi-fei, ZHANG Xiao-jing, WANG Hai. Low-velocity impact response of composite laminate and its relationship with damage parameters[J]. Chinese Journal of Solid Mechanics,2013,34(1):63-72.

[10] 王仁鵬，陳普會，沈真.準靜態壓痕力作用下復合材料層壓板的損傷阻抗分析[J].復合材料學報，2008，25(3)：149-153.

WANG Ren-peng, CHEN Pu-hui, SHEN Zhen. Damage resistance analysis of composite laminates subjected to quasi-static indentation[J]. Acta Materiae Compositae Sinica,2008,25(3):149-153.

[11] 古興瑾，許希武.復合材料整體化加筋壁板高速沖擊損傷數值模擬[J].航空學報，2012，33(2)：258-272.

GU Xing-jin, XU Xi-wu. Numerical simulation of damage in stiffened integral composite panels under high velocity impact[J]. Acta Aeronautica et Astronautica Sinica,2012,33(2):258-272.

[12] 嚴實，趙金陽，陸夏美，等.基于聲發射技術的三維編織復合材料低速沖擊損傷分析[J].材料工程，2014,(7):92-97.

YANG Shi, ZHAO Jin-yang, LU Xia-mei,et al. Low-velocity impact response of 3D braided composites by acoustic emission[J]. Journal of Materials Engineering,2014,(7):92-97.

[13] JOHNSON K L. Contact Mechanics[M]. New York:Cambridge University Press,1985.

[14] HAGENBEEK M,HENGEL V C, BOSKER O J, et al. Static properties of fiber metal laminates[J]. Applied Composite Materials,2003,(10):207-222.

[15] 伊鵬躍，于哲峰，汪海.復合材料層合板低速沖擊剛度退化方案研究[J].力學季刊，2012，33(3)：469-475.

YI Peng-yue, YU Zhe-feng, WANG Hai. Stiffness degradation methodology for low-velocity impact simulation in composite laminate[J]. Chinese Quarterly of Mechanics,2012,33(3):469-475.

[16] 張麗，李亞智，張金奎.復合材料層合板在低速沖擊作用下的損傷分析[J].科學技術與工程，2010，10(5)：1170-1174.

ZHANG Li, LI Ya-zhi, ZHANG Jin-kui. Low-velocity impact damage analysis in composite laminates[J]. Science Technology and Engineering,2010,10(5):1170-1174.

[17] LINDE P, PLEITNER J, BOER H, et al. Modeling and simulation of fiber metal laminates[A]. ABAQUS Users Conference[C]. California:Abaqus Inc,2004.421-439.

Connection of Low-velocity Impact Response and Impact Energy of Stiffened Composite Panel

SHI Xiao-peng,LI Shu-lin,CHANG Fei, BIAN Dong-liang,YIN Jun-jie

(Aeronautics and Astronautics Engineering College, Air Force Engineering University,Xi’an 710038,China)

Based on the finite element software of ABAQUS, with Hashin damage criteria an effective low-velocity impact model of stiffened composite panel was established . The effects of contact pressure, internal energy and damage dissipation energy on the impact response were analyzed. The results show that the peak of contact pressure moves forward and the different value of internal energy and damage dissipation energy becomes bigger with the increasing of impact energy. Meanwhile, the impact test results indicate that the damage degree is direct proportion with impact energy in the low-velocity impact process. Contrast of damage area between finite element analysis and test indicates that both of them fit better.

stiffened composite panel;impact response;finite element analysis;damage area;impact energy

10.11868/j.issn.1001-4381.2015.04.010

TB332

A

1001-4381(2015)04-0053-06

2013-12-14;

2014-09-11

李曙林(1959-)，男，教授，博士生導師，從事專業：飛機結構強度與使用可靠性，聯系地址：陜西省西安市灞橋區灞陵路一號飛行器與動力工程教研部(710038)，E-mail：l.s.lin2008@163.com