多重填補法在任意缺失隨訪資料中的應用*
同濟大學醫學院預防醫學教研室(200092) 鄒莉玲吳娟麗 李 覺
多重填補法在任意缺失隨訪資料中的應用*
同濟大學醫學院預防醫學教研室(200092) 鄒莉玲△吳娟麗 李 覺
目的比較任意缺失模式下不同填補方法在隨訪資料缺失數據中的多重填補效果。方法結合我國外周動脈疾病患者踝臂指數(ankle brachial index,ABI)等基線及六年隨訪數據,通過SAS9.3/MI過程,分別采用馬爾可夫鏈蒙特卡羅(markov chain monte carlo,MCMC)、回歸分析、判別分析(discriminant analysis)和logistic回歸等方法,實現生存時間、生存結局變量缺失值的填補,并作綜合分析及比較。結果得到不同填補方法、不同填補次數多重填補后的生存時間和結局變量完全數據集,并對總體參數作出估計和統計,計算各次填補效率等綜合評價指標。結論對于多次隨訪資料中的連續性變量生存時間,采用回歸分析方法填補效率較高,填補效率隨著填補次數增加而增大,對于缺失率小的變量填補效率更高。
多重填補MI 任意缺失模式 缺失數據 隨訪研究
數據缺失是實驗研究和調查研究中普遍存在的問題,數據缺失會增加統計分析任務的復雜性,降低工作效率,甚至造成結果偏倚。數據缺失特征一般可根據缺失機制、缺失模式兩種方法進行分類[1-4]。按缺失機制分為:(1)完全隨機缺失(missing completely at random,MCAR),缺失現象完全隨機發生,與自身或其他變量的取值無關。該缺失機制在實際應用中較少存在。(2)隨機缺失(missing at random,MAR),是指缺失數據的發生與數據集中其他無缺失的完全變量的取值有關。MAR是最常見的缺失機制。(3)非隨機缺失(missing not at random,MNAR),是指數據的缺失不僅與其他變量的取值有關,也和自身有關。這種缺失大都不是由偶然因素所造成的,缺乏有效的處理方法[1-3]。按數據缺失模式分為:(1)單調缺失模式:對數據集進行適當的行列變換后,可以得到這樣一個矩陣,即呈現出一種層級缺失的模式,矩陣中的元素yj缺失時,則對任意的P≥j,元素yp也是缺失的。(2)任意缺失模式:數據缺失具有隨意性,沒有任何規律可循,即使通過行列變換也無法看出任何規律[1-3]。
在20世紀70年代首先由Donald B.Rubin提出的多重填補(multiple imputation,MI)方法被認為是解決數據缺失問題的首選方法[2-3],該方法通過多次填補產生若干個完整數據集并用于綜合分析,可反映出由于數據缺失造成的統計推斷結果的不確定性。隨著計算方法和軟件技術的成熟,該方法被越來越多地應用于生物醫學、社會科學及其他許多領域。本文擬采用SAS9.3/MI過程中的MCMC、回歸(regression)、logistic回歸、判別分析(discriminant analysis)等方法[9],實現各種類型變量任意缺失值的填補,并對各填補方法進行比較和評價。
資料與方法
1.資料
(1)資料來源
本文所用數據來源于國家自然科學基金項目:我國外周動脈疾病的危險因素及心血管疾病死亡風險預測模研究。2004年7月1日至2005年1月16日期間完成包含踝臂指數(ABI)的基線資料收集。對每位研究對象測量靜態ABI,并由專業人員采用問卷調查表記錄研究對象的人口學資料、生活行為習慣、既往史和現病史、體格檢查及實驗室檢查結果。此后分別于2006年1月、2008年1月和2010年9月開展三次隨訪調查,收集研究對象的心血管事件發生、死亡結局和生存時間等數據。本文選用數據核查后的3606例研究對象的性別、年齡、身高、體重、ABI以及三次隨訪獲得的生存時間T值(T1、T2、T3)及結局變量S值(S1、S2、S3)作為欲填補的數據集。
(2)數據特征
ABI隨訪數據中的性別、年齡、身高、體重、ABI和第一次隨訪S1、T1為完全變量(N=3606)。其中性別(Gender)和第一次隨訪結局(S1)為二分類變量,男性患者1912例(53.02%),第一次隨訪死亡308人(8.54%)。第二次隨訪和第三次隨訪的結局變量(S2、S3)和生存時間(T2、T3)為不完全變量,S2、S3和T2、T3的數據缺失頻數分別為522(14.48%)、535(14.84%)、559(15.50%)和1148(31.84%),見表1,表2。
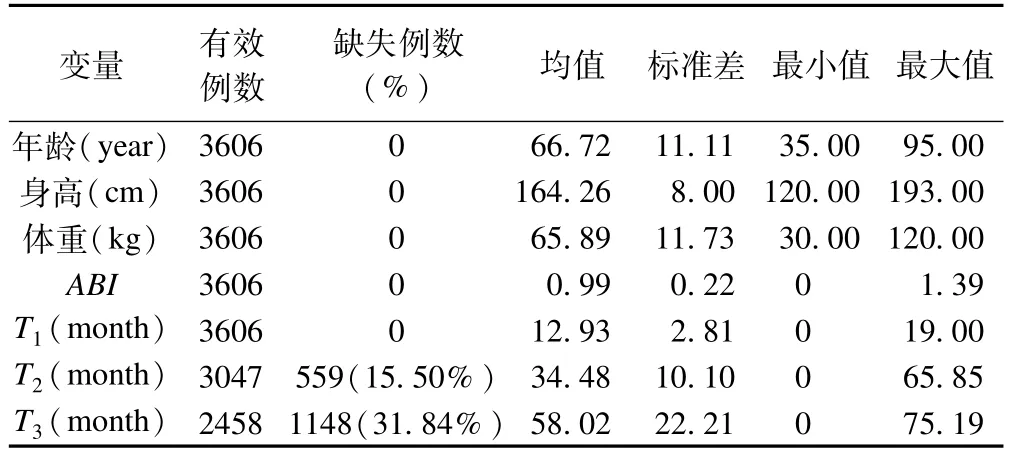
表1 ABI隨訪數據中各連續變量的統計描述特征
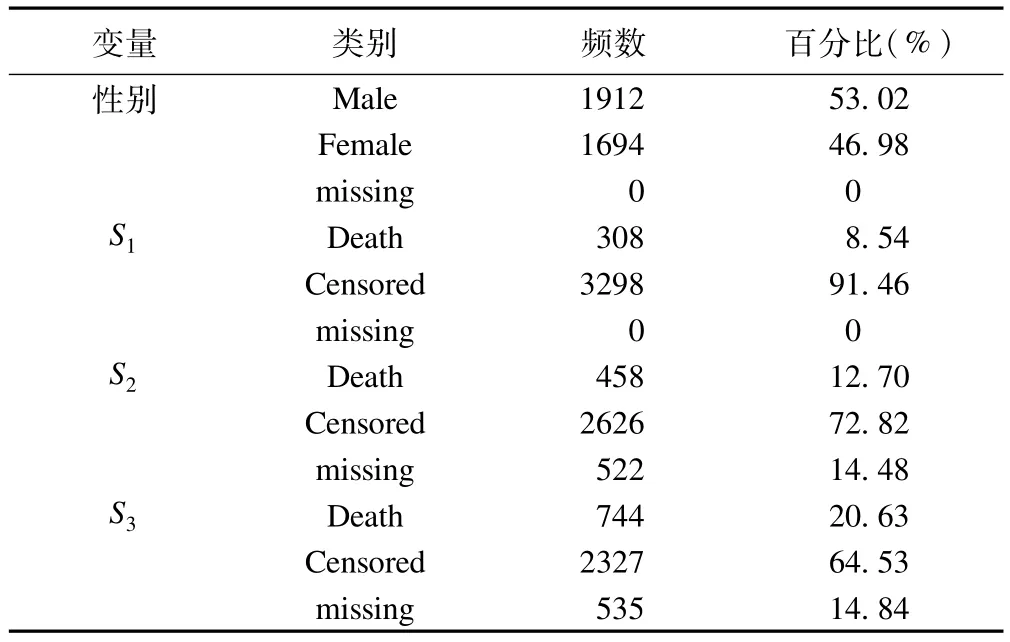
表2 ABI隨訪數據中各分類變量的統計描述特征
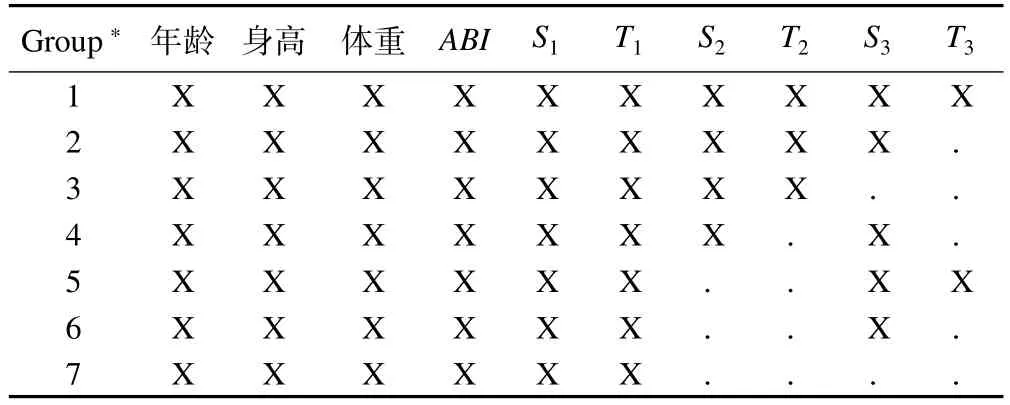
表3 數據缺失模式
表3為數據缺失的模式。對該矩陣進行任意的行列變換都無法呈現層級缺失的模式,因此本資料數據缺失為任意缺失模式。
2.方法
分別采用SAS9.3/MI過程中的MCMC、FCSREG、FCS-Discrim、FCS-Logistic方法進行多重填補[9],填補次數(m)依次設置為2、5、10次。并對填補后的多個數據集進行綜合分析和結果比較,連續性變量計算各次填補后的填補效率、總體參數的均值Q和方差σ2、可信區間范圍,分類變量計算各事件頻率。
假定某不完全變量的總體參數為Q和σ2,多重填補的次數為m。則每次多重填補后可得到m個Q和σ2的點估計值,進行綜合分析即可得到總體均值Q和方差σ2的估計和推斷[5,7]。

結 果
將不同填補方法、不同填補次數用于任意缺失模式下的第二次和第三次隨訪的結局和生存時間變量進行數據填補,再采用以上各指標作出總體參數估計和推斷結果(表4、表5和表6),并給出綜合評價指標填補效率的計算結果(表7)。

表4 不同方法填補后的生存時間變量方差及相關信息
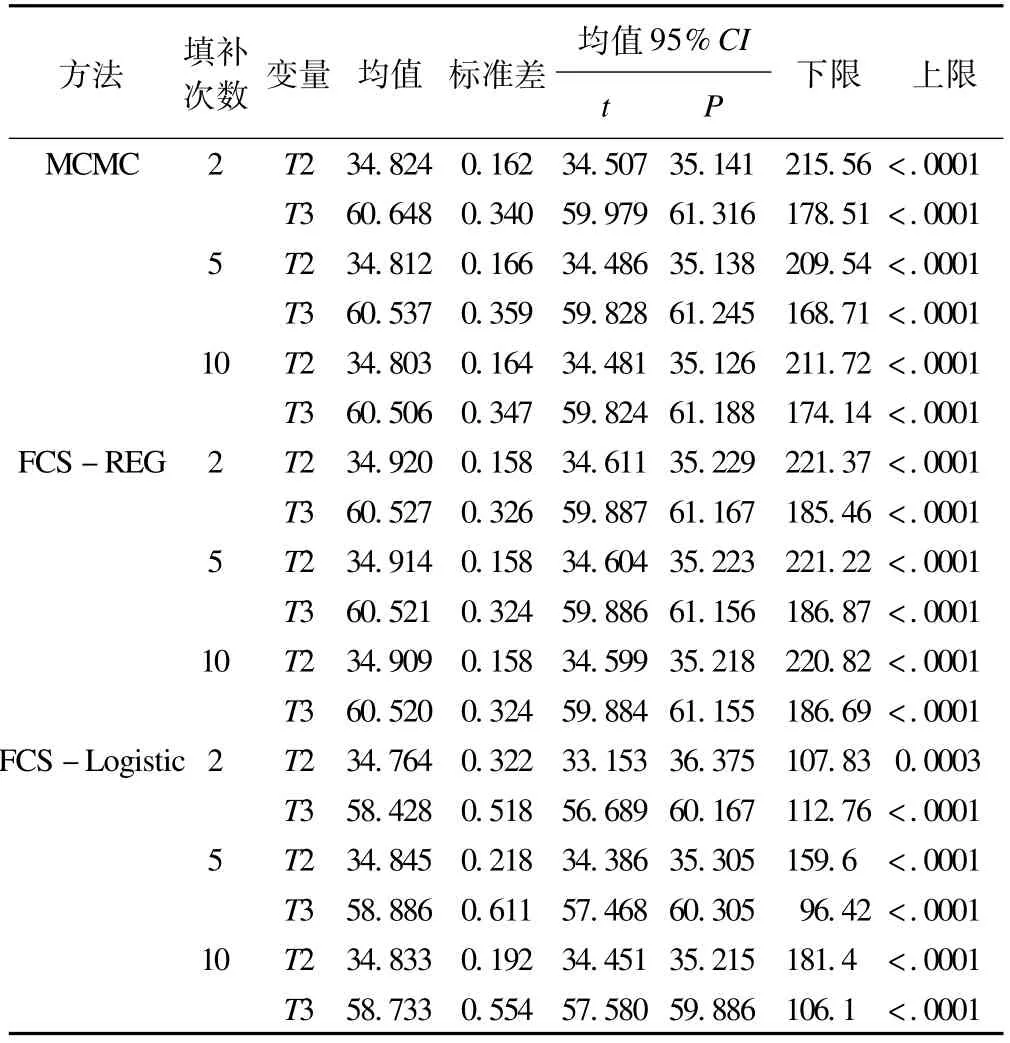
表5 不同方法填補后的生存時間變量參數估計
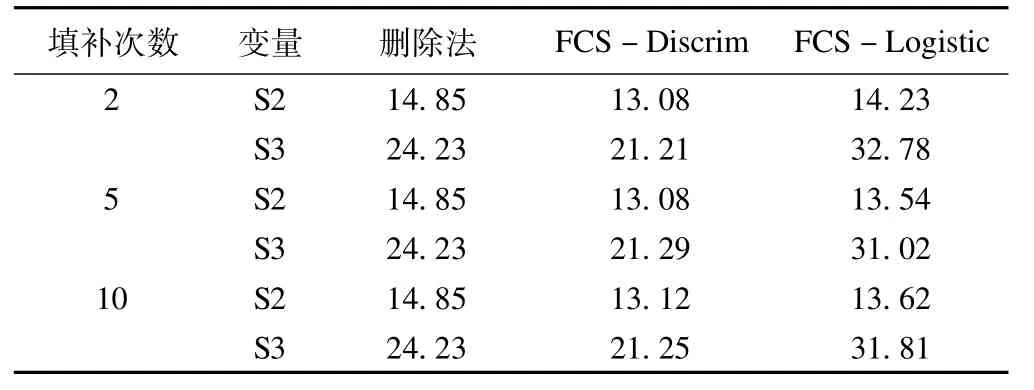
表6 不同方法填補與刪除法的結局變量死亡頻率(%)
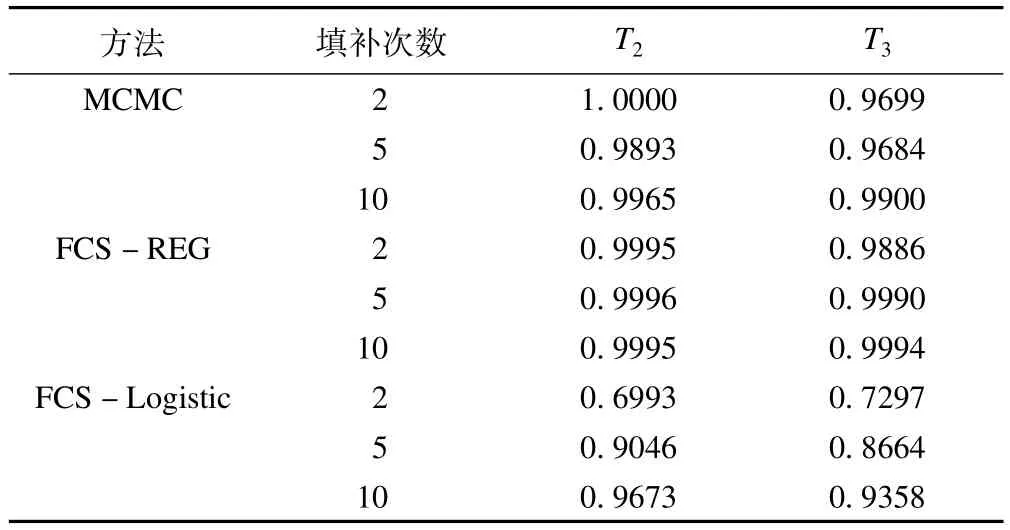
表7 不同方法填補的效率RE計算表
討 論
本研究通過采用MCMC、回歸分析、logistic回歸和判別分析等MI填補方法,對外周動脈疾病ABI基線及多次隨訪資料中任意缺失模式下的生存時間和結局變量進行缺失數據填補,結果提示對于連續性變量(生存時間),回歸分析方法填補效率最高,效率隨著填補次數增加而增大,并且對于缺失比例較小的變量填補效率更高,這與其他文獻結論一致。本文還應用logistic回歸和判別分析等填補方法,對二分類變量(生存結局)的缺失數據進行了多重填補并加以比較。由于兩變量的缺失率都很小(S2=14.48%,S3=14.84%),采用兩種填補方法得到的總死亡頻率估計值和刪除法的結果都比較接近,填補次數增大對結果影響不大。對于二分類變量,有研究者認為一般不必進行填充,缺失較少時采用成組刪除法簡單易行、準確高效,但是當缺失率較大(缺失率>40%)時,為滿足數據分析的需要,有時可以根據數據缺失機制或模式選用不同方法進行填充[5]。本文由于缺乏模擬數據的研究結果,尚無法得出該結論。
在隨訪研究中,由于研究周期較長,往往后續隨訪調查數據的缺失較為普遍,而生存時間和結局變量由于其在生存分析中的重要作用不可或缺,數據缺失較大時對結果的影響較大,有必要對實際資料結合缺失模式和缺失機制,采用相應的數據填補方法進行填補。MI法由于其填補效果高、參數估計結果更穩定和接近真值[8],而越來越受到國內外廣大研究者的關注和推崇。目前,SAS9.3已經將MI和MIANALYZE作為兩個正式過程納入其中[9],并且增加了FCS方法用于不同類型多變量條件下的各種缺失數據填補,進一步豐富了MI填補的方法選擇。
1.Abraham,Todd W,Russell,et al.Missing data:a review of current methods and applications in epidemiological research.Current Opinion in Psychiatry,2004,17(4):315-321.
2.James M,Robins,Wang N.Inference for imputation estimators.Biometrika,2000,87(1):113-124.
3.Little RJ,Rubin DB.Statistical Analysis with Missing Data.New York:John Wiley&Sons,1987.
4.張橋,李寧,張秋菊,等.任意缺失模式缺失數據不同填補方法效果比較.中國衛生統計,2013,10(35):690.
5.茅群霞.缺失值處理統計方法的模擬比較研究及應用:碩士畢業論文.
6.花琳琳.施念,楊永利,等.不同缺失值處理方法對隨機缺失數據處理效果的比較.鄭州大學學報:醫學版,2012,47(3):315.
7.Combining Inferences from Multiple Imputed Data Sets.SAS/STAT 9 User′s Guide,North Carolina:SAS Institute Inc,2002:211-213.
8.Schafer JL,Maren kO.Multiple imputation for multivariate missing-data problems:a data analysis's perspective.Multivariate Behavioural Research,1998,33:545.
9.http://support.sas.com/rnd/app/stat/procedures/mi.html.
(責任編輯:郭海強)
Multiple Imputation Method Used in Arbitrary Missing Follow-up Data
Zou Liling,Wu Juanli,Li Jue(Department of Preventive Medicine,Medical School,Tongji University(200092),Shanghai)
ObjectiveTo evaluate the multiple imputation effect of different imputation methods in arbitrary missing data of follow-up research.MethodsUsing different methods including Markov chain Monte Carlo(MCMC),Regression,discriminant analysis and logistic regression and SAS9.3/MI process,to make the comprehensive analysis and comparison for missing values imputation.The real data come from a6 years follow-up research including peripheral arterial disease patients′information and ankle brachial index(ABI)data.ResultsIncluding population parameters estimation and statistics inference of continuous variables,frequency calculation of classified variables,based on different imputation methods and imputation numbers.ConclusionIn the continuous variables such as survival time,Regression method has the largest imputation efficiency,and the efficiency increases with the increase of imputation number and decrease of the missing rate.
Multiple imputation MI;Arbitrary missing model;Missing data;Follow-up study
*國家自然科學基金青年項目(81102203/H2611)
△通信作者:鄒莉玲,E-mail:zouliling_59@tongji.edu.cn

