隨機區組設計多個樣本多重比較的非參數q檢驗方法的SAS實現

蘭州大學公共衛生學院流行病與衛生統計研究所（730000） 高文龍劉小寧 李生娟 申希平

隨機區組設計多個樣本多重比較的非參數q檢驗方法的SAS實現

蘭州大學公共衛生學院流行病與衛生統計研究所（730000） 高文龍△劉小寧 李生娟 申希平

當隨機區組設計多個相關樣本總體分布未知或分布不滿足正態性，這樣的資料無法利用隨機區組設計資料的方差分析來解決。Friedman M檢驗是一種隨機區組設計資料秩轉換的非參數檢驗方法，可用來推斷這些樣本所來自的多個總體分布是否有差別。然而，該方法僅推斷了這多個相關樣本總體分布的差別。如果經Friedman M檢驗這幾個樣本總體分布確有差別，要推斷哪兩組樣本總體分布間存在差別，此時可以利用秩轉換的多個相關樣本兩兩比較的q檢驗來實現。在一些常用的統計軟件中均未提供在這種情形下q檢驗的實現模塊筆者用SAS軟件實現了Fridman M檢驗有差別后兩兩比較的q檢驗方法。

Friedman M和q檢驗方法的實現原理［1］

Friedman M檢驗原理：設隨機區組設計資料區組個數為n，相關樣本個數為g。首先，將每個區組的數據由小到大分別編秩，遇數據相等者取平均秩；然后，計算各樣本的秩和Ri，平均秩各為此時，可求得統計量M值。

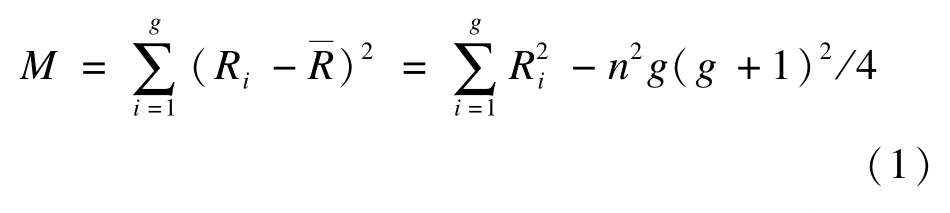
當g＞4，或者g＝4且n＞5，或者g＝3且n＞9時，可近似用下面χ2公式來檢驗：

q檢驗原理：對于這g個相關樣本，n個區組資料，若n個數較多，可按下式求第i個樣本和第j個樣本比較的q值。

實例與SAS程序

本文采用文獻［1］提供的實例。8名受試對象在相同實驗條件下分別接受4種不同頻率聲音的刺激，他們的反應率（%）資料見表1。問4種頻率聲間刺激的反應率是否有差別？

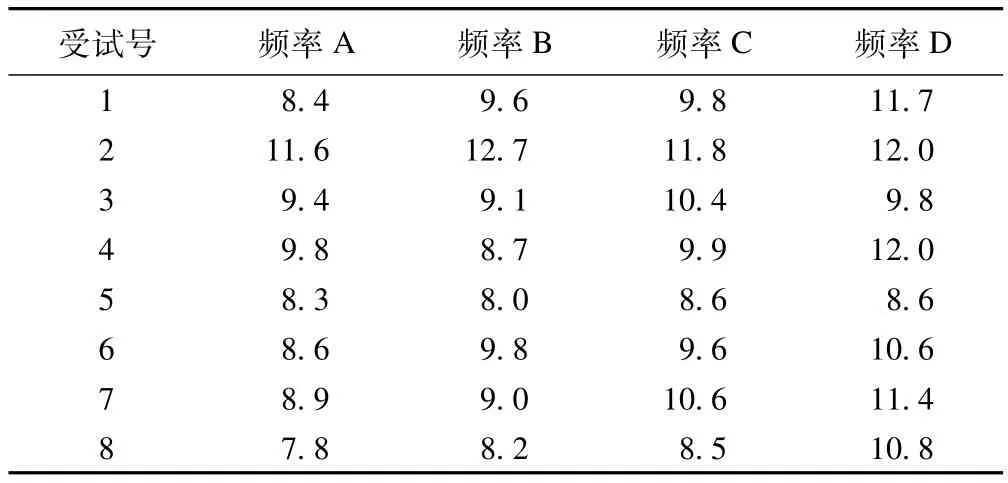
表1 8名受試對象對4種不同頻率聲間刺激的反應率（%）比較

SAS實現程序如下［1－2］：

△通信作者：高文龍，E-mail：gaowl＠lzu.edu.cn