年估計百分比變化與平均增長速度在公共衛生領域中的應用比較

張榮強李鳳英

年估計百分比變化與平均增長速度在公共衛生領域中的應用比較

張榮強1李鳳英2

目的本文采用年估計百分比變化（the estimated annual percentage change，EAPC）和平均增長速度分析和探討咸陽市2005－2012年乙肝、流行性腮腺炎發病率的動態變化規律，旨在尋找最佳的統計預測指標。方法采用描述性流行病學方法進行資料收集，經線性擬合計算乙肝和流行性腮腺炎發病率的年估計百分比變化（EAPC）和平均增長率，比較其各自的優缺點。結果乙肝發病率EAPC（%）＝100×（e-0.127－1）＝－11.93%，EAPC 95%CI為－13.13%～－10.71%（P＜0.05）；流行性腮腺炎發病率EAPC（%）＝100×（e0.083－1）＝8.65%，EAPC 95%CI為－3.26%～19.86%（P＜0.05）。結論公共衛生及統計實踐中，進行預測時應選擇科學的方法，可首選年估計百分比變化（EAPC）。

乙肝 流行性腮腺炎 發病率 平均增長率 年估計百分比變化

在公共衛生工作中，常常需要根據相關現象的升降變化規律，作出預測，以正確地制定短期計劃或中長期規劃。但在實際衛生工作中，單純采用平均增長速度，穩定性不理想，并不能準確揭示相關現象的變化規律，亟需探索更加精確和客觀的預測方法［1-3］。故本文通過實例分析比較年估計百分比變化（the estimated annual percentage change，EAPC）和平均發展速度，預期為公共衛生實際工作提供參考。

資料與方法

1.材料來源

咸陽市2005年1月－2012年12月乙肝和流行性腮腺炎病例個案資料來自于國家疾病監測信息報告管理系統，咸陽市人口資料來自咸陽市統計信息網。

2.病例診斷標準及界定

根據中國疾病預防控制中心制訂的“全國乙肝及流行性腮腺炎監測方案”，本文將病例界定為臨床診斷病例、實驗室診斷病例和病原攜帶者。

3.研究方法

（1）描述性研究

采用描述性流行病學研究分析咸陽市2005－2012年乙型肝炎及流行性腮腺炎的發病率現狀及其變化趨勢。

（2）年估計百分比變化（EAPC）的計算

將時間變量（年份）作為自變量x，將咸陽市2005－2012年乙肝、流行性腮腺炎發病率行自然對數轉化之后的新變量為因變量y，擬合直線，即：y＝b＋mx，其中，y＝ln（發病率）；進一步計算年估計百分比變化，EAPC＝100×（em-1）。計算年估計百分比變化的前提是假設發病率在整個觀察期內的變化持續穩定。為了排除隨機因素對EAPC的影響，故對EAPC進行統計學的假設檢驗。對EAPC的假設檢驗等同于對擬合直線斜率的假設檢驗，即：若直線存在，則擬合直線的斜率m存在，進而認為EAPC有效，換言之，將對EAPC的假設檢驗轉化為對擬合直線斜率m的t檢驗。t值為t＝m／sm（m為直線斜率；sm為斜率m的標準誤），自由度v為時間變量的個數減去2［4-7］。由于斜率m的標準誤對擬合直線斜率及EAPC的影響，故應進一步表示出EAPC的95%可信區間。

（3）平均增長速度

在實際衛生工作中，平均增長速度表示發展規律的常用指標之一，其計算方法為幾何法和累積法，幾何法由于簡單易算而最為常用；累積法計算相對復雜，實際工作中幾乎不使用。本研究采用幾何法計算平均增長速度，計算公式為：平均增長速度式中：a0為基期指標，an為第n年指標［5-6］。

4.統計分析

運用SPSS 19.0及Sigmaplot 10.0等統計及作圖軟件進行相關的統計操作；檢驗水準為α＝0.05。乙肝、流行性腮腺炎的發病率變化均采用平均增長速度（幾何平均法）與年估計百分比變化兩種方法分析，將結果作對比說明，以期探討實際衛生工作中較客觀的預測指標。

結 果

1.咸陽市2005－2012年乙肝、流行性腮腺炎發病率EAPC

以年份為自變量x，以ln（發病率）為因變量y，行簡單線性擬合。對于乙肝發病率，獲得方程：y＝257.805－0.127x（t＝17.117，P＝0.000；R2＝0.980），提示方程具有統計學意義，且擬合效果較好，故EAPC（%）＝100×（e-0.127－1）＝－11.93%，EAPC 95%CI為（－13.13%～－10.71%）。流行性腮腺炎發病率，獲得方程：y＝－166.708＋0.083x（t＝1.411，P＝0.208；R2＝0.249），方程無統計學意義，故EAPC（%）＝100×（e0.083-1）＝8.65%，EAPC 95%CI為（－3.26%～19.86%）。根據EAPC的含義，有統計學意義的年估計百分比變化（EAPC）表示發病率的穩定變化速度，其正負號表示變化的方向。因此，可以認為：2005－2012年，咸陽市乙肝發病率具有穩定的下降趨勢，以平均每年11.93%的速度下降（P＜0.05）；而流行性腮腺炎的發病率以大約平均每年8.65%的速度升高（P＞0.05），但該變化趨勢并不穩定，未排除隨機因素對發病率變化的影響，因此，咸陽市流行性腮腺炎發病率變化尚無確切結論，仍需進一步研究證實。

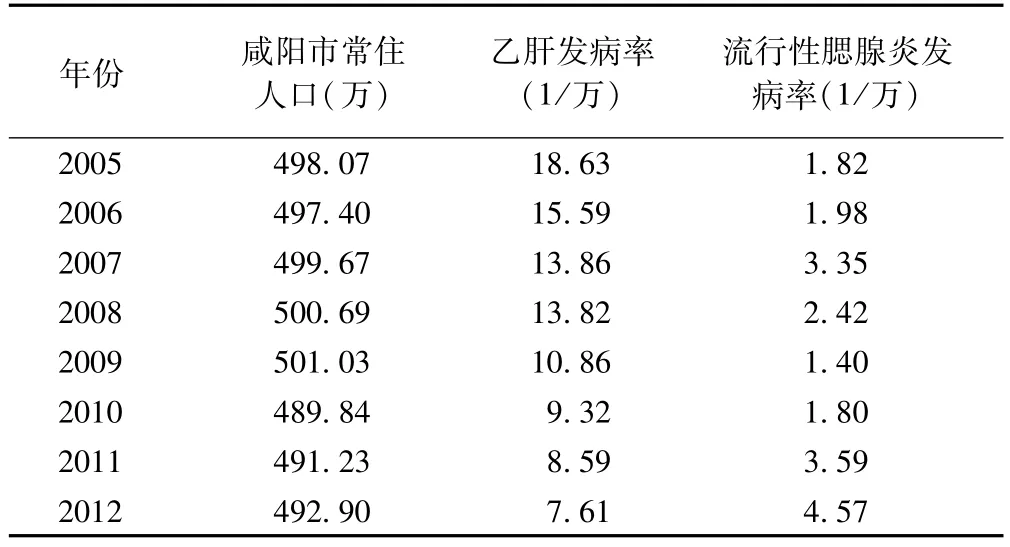
表1 咸陽市2005－2012年乙肝、流行性腮腺炎發病概況

2.咸陽市2005－2012年乙肝、流行性腮腺炎發病率平均增長速度

討 論

1.兩種分析結果

對于流行性腮腺炎發病率而言，采用平均增長速度和EAPC計算的結果相差甚遠，意義相反。EAPC提示其變化趨勢不穩定，得出結論尚早；而平均增長速度為14.06%，提示咸陽市流行性腮腺炎的發病率增長速度較快。根據擬合直線的特點分析，流行性腮腺炎發病率與時間的線性擬合效果不佳（R2＝0.249），提示其受到隨機誤差的影響較大，而假設檢驗的P＞0.05，尚不能排除流行性腮腺炎發病率不變化的可能性，這一關系與實際情況較為接近。因此，本研究認為：流行腮腺炎發病率的平均增長速度為14.06%，表示其變化規律誤差較大，代表性較差。另一方面，2005－2012年，乙肝發病率的變化趨勢穩定（見表1），經線性擬合后，EAPC＝11.93%（P＜0.05），而年均增長率為12.01%，因此，由此可以推測：當某個現象變化趨勢比較穩定的情況下，EAPC與年均增長率結果是一致的。

綜上，采用EAPC評估某現象的年均變化速度，對結果的隨機性進行了假設檢驗，在邏輯上更嚴謹，結合表1乙肝發病率變化可以發現：EAPC更接近客觀實際。因此，如果某事件在一段時期內的變化不穩定，則表現為波動比較大，不適合對它的發展趨勢進行分析，更不適合計算平均增長率，雖然EAPC計算復雜，但能更客觀的反應事件的實際變化情況。

2.EAPC的優點

與平均增長速度相比，EAPC主要有以下兩個優點：

（1）平均增長速度只考慮了觀察起始值（a0）和終端值（an），未考慮觀察期中間的數值，因此計算相對粗略。EAPC是依據時間變量及其對應的每個觀察值的自然對數擬合直線，然后根據直線的斜率計算，每個觀察值對EAPC計算結果均有貢獻，因此，EAPC計算過程中，信息利用率較理想。

（2）平均增長速度計算完畢后，一般不經過任何統計學的檢驗即可認為結果有效，這實際與平均增長速度要求數據呈幾何增長的前提矛盾，這是實際工作中，平均增長速度應用過程中的一個誤區。國內的許多學者也逐漸意識到，平均增長速度應該結合時間序列隨機性檢驗，以了解根據觀察值所計算的平均變化速度所代表的某種趨勢是否由隨機誤差引起，方能做出結論［8-9］。EAPC是以統計學的直線擬合理論為基礎的，統計學檢驗是其計算過程不可或缺的一部分，是將前提假設（變化趨勢穩定）與統計學假設檢驗自然結合的產物。經假設檢驗，若有統計學意義，方可認為該觀察期內，平均每年以此變化量變化是有效的。從統計學邏輯而言，EAPC更嚴謹、更科學。

3.EAPC在公共衛生工作中的應用

（1）國內用EAPC表示某現象的平均變化規律的報道較少，常用幾何均數法計算平均增長速度；國外學者多用EAPC表示疾病的發病率、死亡率的長期變化趨勢，EAPC的用途更加廣泛［3－4，10］。

（2）EAPC在公共衛生工作中可有以下方面的應用：揭示某現象發展變化的本質特征，跟蹤其變化趨勢；衡量某現象發展快慢的指標，可橫向比較，亦可歷史對比；可據此預測未來的發展，科學地指導衛生工作。

綜上，公共衛生及統計實踐中，進行預測時應選擇科學的方法［11－12］。本研究認為，采用變化速度時應注意以下幾點：首先考慮數據的變化規律，如果數據呈幾何級增長，變化趨勢穩定，平均增長速度與EAPC較接近；結果應經過假設檢驗以考察隨機因素的作用；若能充分考慮上述兩點，應首選年估計百分比變化（EAPC）。

1.Siesling S，JA van Dijck，O Visser，et al.Trends in incidence of and mortality from cancer in The Netherlands in the period 1989-1998.Eur J Cancer，2003，39（17）：2521-2530.

2.Fay MP，RC Tiwari，EJ Feuer，et al.Estimating average annual percent change for disease rates without assuming constant change.Biometrics，2006，62（3）：847-854.

3.Zhou Y，TD Baker，K Rao，et al.Productivity losses from injury in China.Inj Prev，2003，9（2）：124-127.

4.Tushar Patel.Worldwide trends in mortality from biliary tract malignancies.BMC Cancer，2002，2：10.

5.方積乾.衛生統計學.第5版.北京：人民衛生出版社，2003：44.

6.孫振球.醫學統計學.第2版.北京：人民衛生出版社，2005：108.

7.Yu D，Manderson L，Yuan L，et al.Is equity being sacrificed Willingness and ability to pay for schistoso miasis control in China.Health Policy Plan，2001，16（3）：292-301.

8.Lee K.Financing health services in China：Adapting to economic reform：By SL Tang，G Bloom，XS Feng，H Lucas，XY Gu and M Segall，Brighton，Institute of Development Studies.IDS Research Report 26，1994.Social Science＆Medicine，1997，45（10）：1601-1602.

9.張振東，田衛文，劉俊玲.累積法求平均速度在動態數列分析中的運用.地方病通報，2006，21（6）：68-69.

10.Henneberry J.States Face Increased Expenditures for Pharmaceuticals. 2000.www.nga.org／Files／pdf／000203PHARM.pdf.

11.張榮強，裴泓波，王敏珍，等.應用回歸模型預測食管癌住院費用.中國衛生統計，2009（4）：417-418.

12.黃娟.趨勢季節模型在醫院門診診療人數預測中的應用.中國衛生統計，2009，26（6）：660.

（責任編輯：丁海龍）

1.陜西中醫學院公共衛生系（712046）

2.陜西省咸陽市疾病預防控制中心