基于魯棒H∞控制的運載火箭姿態控制系統設計

薛 宇 高松濤 徐永成 劉玉璽

上海宇航系統工程研究所，上海201109

現役運載火箭動力學數學建模已很成熟，考慮彈性振動以及液體晃動的運載火箭姿態PD控制系統已廣泛應用［1］。但是，新一代運載火箭采用新型發動機，其發動機質量大、轉動慣量大，發動機搖擺點距離伺服機構下支點的距離長，負載頻率低，與全箭彈性頻率之間很可能出現重疊的情況［2］。前蘇聯和美國在該方面研究頗多［3-4］。國內學者也研究了發動機搖擺與全箭動力學特性耦合的關系［5］。同時，新型運載火箭逐漸提出放棄大規模的全箭振動試驗［6］，必將導致火箭動力學模型參數產生較大偏差。為了適應新型運載火箭模型參數不確定性以及模型復雜性，傳統上基于“固化系數法”分段設計PD控制器的控制方法的局限性已顯現，必須尋求新的解決方案。

針對新型運載火箭姿態控制系統的設計，國內外學者都提出了相應的解決方案。甘永梅基于運載火箭剛體運動、彈性振動及外干擾的運載火箭動力學模型進行魯棒自適應控制器設計［7］，但忽略了發動機較低的振動頻率與全箭模態之間的耦合。國外基于H∞控制的飛行器姿態控制系統設計已展開廣泛研究［8］，并發展了基于H2/H∞混合控制的技術，實現了對飛行器姿態更好的穩定控制［9］，但應用于運載火箭姿態控制系統的資料難以查到。

本文采用H∞控制技術，考慮發動機振動與全箭模態可能產生諧振，氣動特性、全箭彈性振動等參數不確定性，液體晃動以及風干擾等外部干擾，按工程實際應用的性能指標設計運載火箭的控制系統。仿真結果表明，魯棒H∞控制技術在運載火箭控制系統設計中有效的消除了高頻抖動，能適應更大范圍內的參數不確定性。

1 運載火箭俯仰通道數學模型

當運載火箭的發動機小，與全箭耦合不嚴重時，式(1)中的質心動力學、繞質心動力學、全箭振動方程以及液體晃動方程能夠滿足工程應用。隨著新型發動機的采用，發動機質量的增加以及搖擺轉動慣量的增加，必須建立發動機振動方程，分析“發動機-伺服機構”回路對全箭模態的影響。

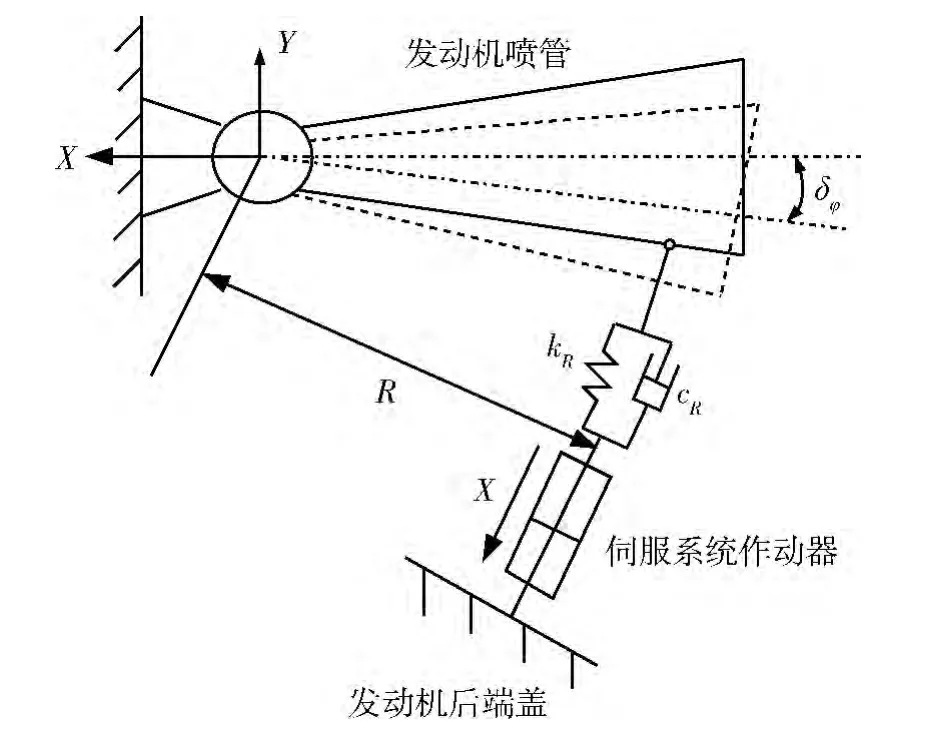
圖1 發動機簡化原理圖

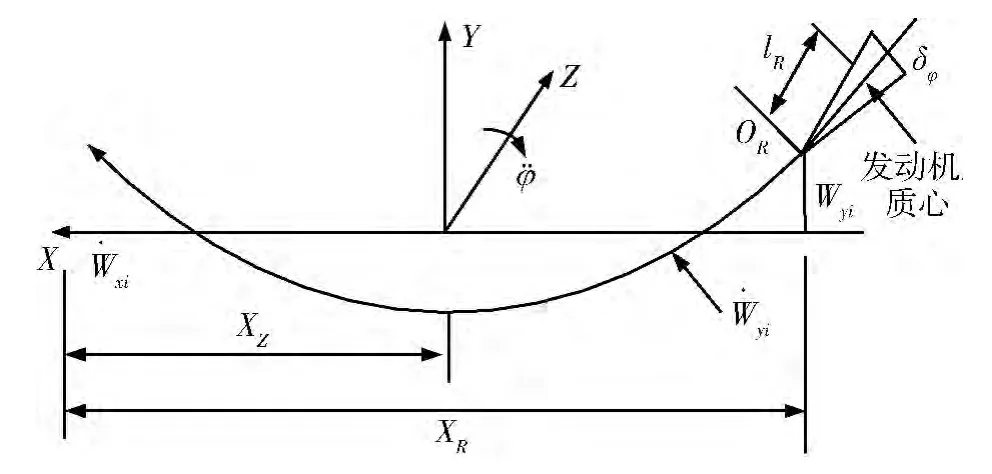
圖2 火箭“剛體-彈性”運動示意圖

則發動機在搖擺點處的慣性負載力矩為

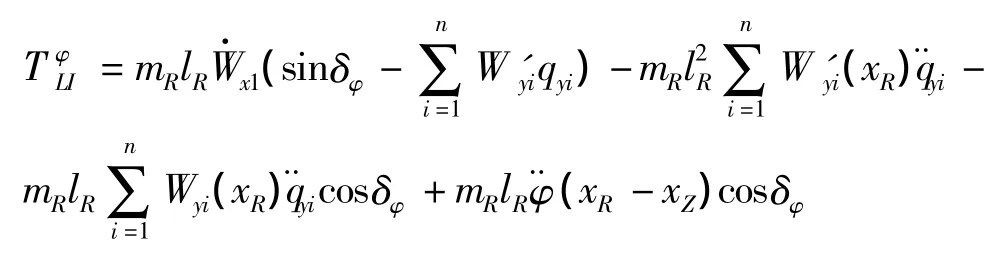
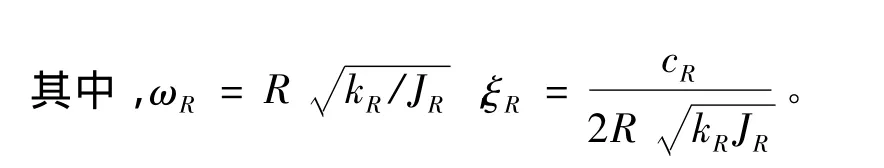
可以看出，在剛度不變，發動機轉動慣量較大時，發動機振動頻率較低，發動機搖擺會與全箭模態相互耦合，必須在控制系統考慮發動機慣性負載力矩。

考慮發動機振動方程的某型運載火箭姿態控制系統反饋控制的結構圖如圖3所示。

火箭的姿態角和角速度可分別由捷聯慣組與速率陀螺測量，由計算機解算出姿態角參數，并按一定的控制率計算出控制擺角，輸出到伺服機構。同時發動機擺角也受到慣性負載力矩的影響。發動機擺角為火箭姿態動力學模型的輸入，整個系統構成完整的閉環反饋控制。

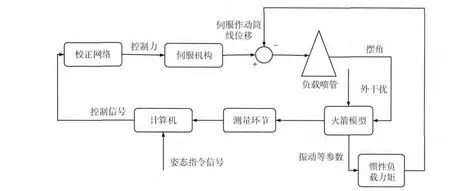
圖3 運載火箭姿態控制系統結構示意圖

2 控制系統設計

2.1 魯棒H∞控制原理

如圖4所示為具有參數不確定性和未建模動態不確定性的系統。

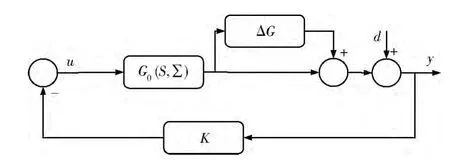
圖4 控制系統框圖

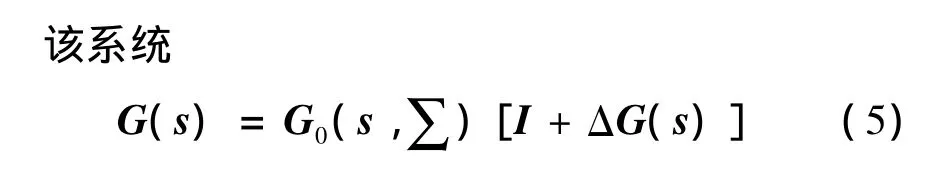
顯然，G0(s，∑)對應于運載火箭的姿態動力學模型，表示具有參數不確定的對象，ΔG為非結構不確定性，表示系統的未建模動態特性。

設具有參數不確定性的被控對象為

式中，ΔA，ΔB2表示A，B2的不確定性。

對于該運載火箭姿控系統，所要求解的控制器滿足

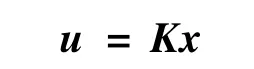
使姿控系統滿足如下設計要求:

1)ω=0時，閉環系統二次穩定;

2)ΔA，ΔB2為0時，A+B2K為穩定陣，且滿足

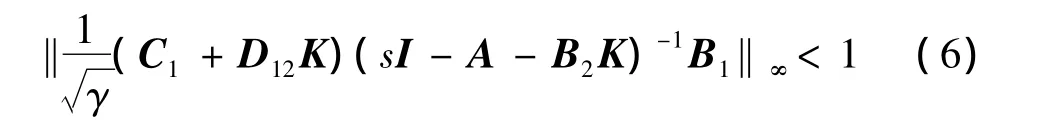
狀態反饋增益矩陣K存在的充分必要條件是

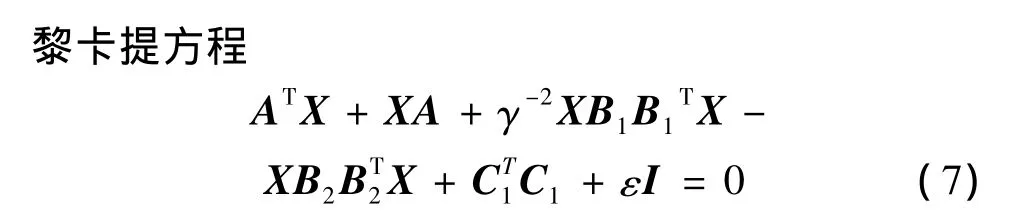
對于一個充分小的常數ε＞0具有正定解X＞0。

本文需選擇合適的加權矩陣C1和矩陣D12，以及參數γ，求解出黎卡提方程，進而求出狀態反饋控制器的增益反饋陣。

2.2 魯棒控制器設計

根據經驗，全箭振動、液體晃動以及發動機舵偏角的二次微分屬于高頻信號，難以建立精確模型，具有較大的參數不確定性。考慮運載火箭剛體運動學方程:

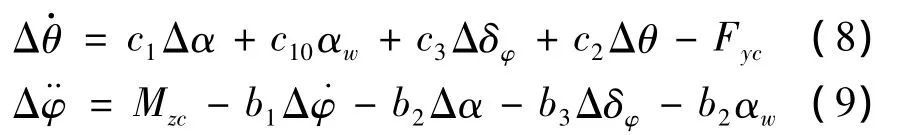
整理成狀態空間方程為:

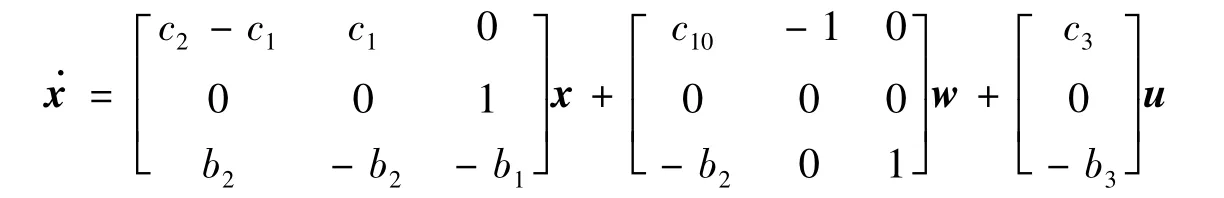
取γ=20，將運載火箭飛行時段分成若干段，分別取飛行時段中某時刻的參數來求解H∞狀態反饋控制器的增益反饋陣K，作為該時段的狀態反饋控制器。

某時刻運載火箭運動方程

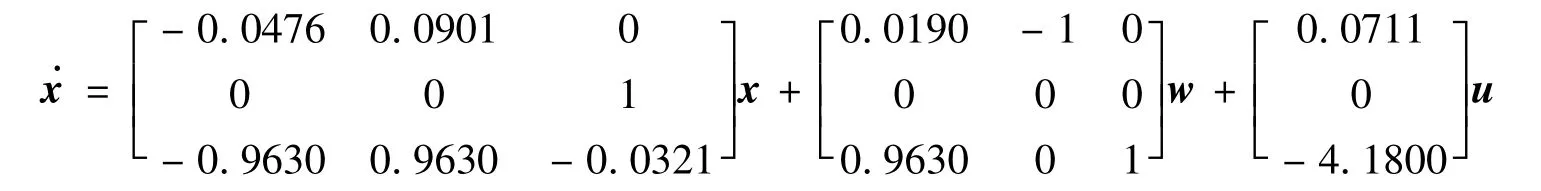
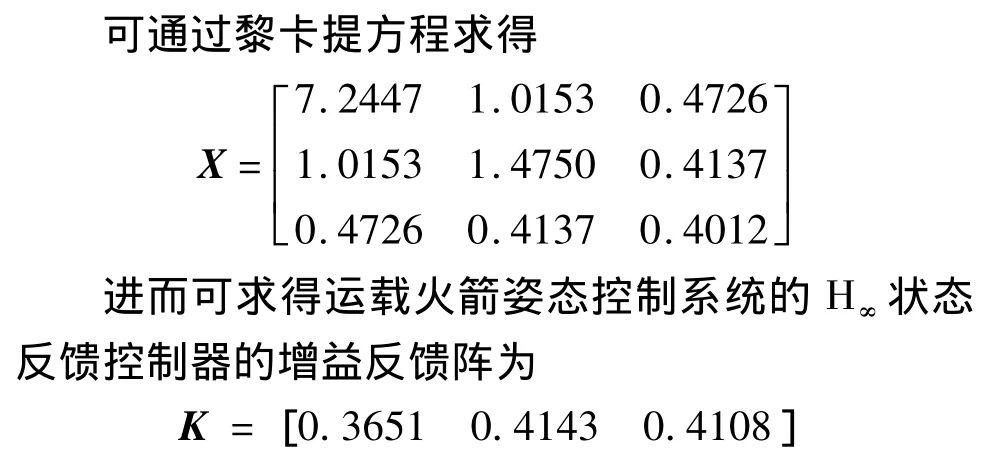
通過上述計算過程，可計算出狀態反饋陣K，使得閉環系統內部穩定。將狀態反饋陣K代入運載火箭剛體數學模型、彈性振動、液體晃動以及發動機振動方程，通過仿真分析驗證狀態反饋陣K是否可行。該運載火箭飛行共分為3段，故設計了3個相應的增益反饋陣K，但整個飛行時段中只設計了一套校正網絡，故可以說明相應的H∞控制器對網絡的依賴程度較低。

3 仿真結果

基于某新型運載火箭動力學模型，以飛行時段的俯仰通道各參數為基礎，考慮彈性振動、液體晃動，并考慮發動機彈性振動方程，分別利用PD控制理論及H∞控制理論設計控制器。該型運載火箭在70s左右經過大風區，即外干擾最大，仿真結果如圖5。

考慮PD控制與H∞控制器的魯棒性，不妨改變氣動參數b2以及彈性參數D3i。工程上參數b2的偏差為 20%，即［0.8b2，1.2b2］;D3i的偏差為 30%，即［0.7D3i，1.3D3i］。當氣動參數 b2及彈性參數 D3i在偏差范圍之內時，仿真結果如圖4。觀測液體晃動，很明顯PD控制下液體具有高頻率晃動，會產生的慣性力，與全箭耦合，對全箭穩定產生不良影響。而H∞控制器很好的控制了液體的高頻率晃動，利于全箭穩定。

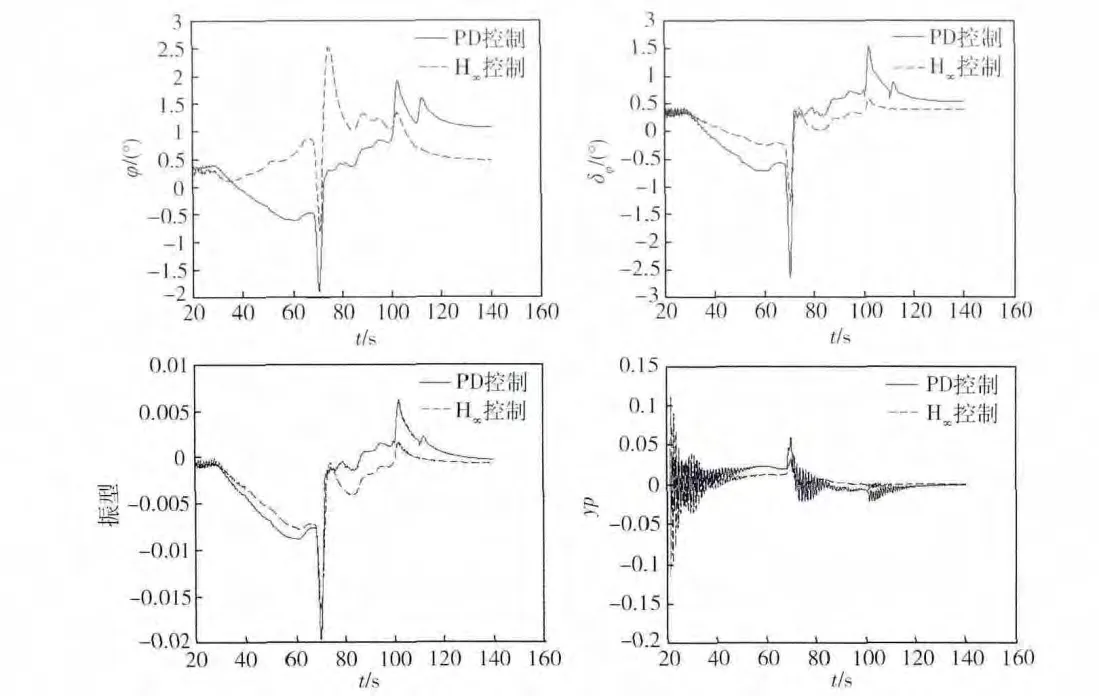
圖5 某型號運載火箭PD控制與H∞控制器仿真結果對比

擴大氣動參數b2及彈性參數D3i的偏差，不妨取參數 b2的偏差為40%，即［0.6b2，1.4b2］，D3i的偏差為 40%，即［0.6D3i，1.4D3i］。當取值分別為0.6b2，1.4D3i，仿真結果如圖6。當取值分別為1.4b2，0.6D3i，仿真結果如圖7。

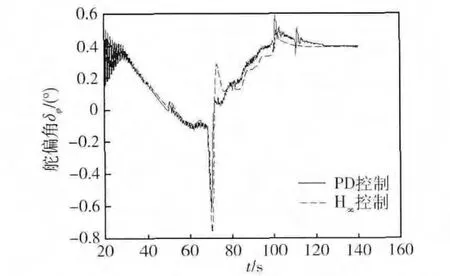
圖6 0.6b2，1.4D3i時PD控制與H∞控制下舵偏角

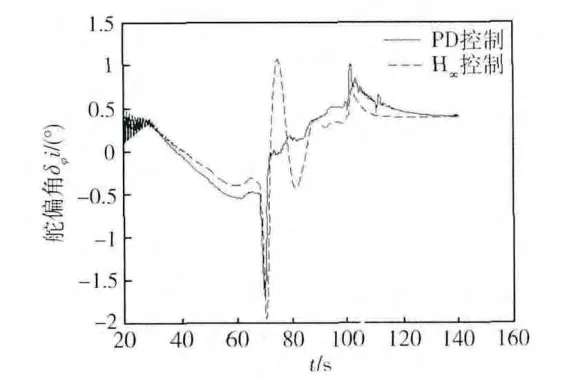
圖7 1.4b2，0.6D3i時PD控制與H∞控制下舵偏角

從仿真結果中可以看出，當不確定參數偏差較大時，PD控制下舵偏角出現高頻抖動，而H∞控制器仿真結果魯棒性較好，有效地消除了高頻抖動，舵偏角曲線更為光滑，適用于工程應用。

綜上，當考慮發動機振動方程，以及參數不確定性較大時，H∞控制器能使該運載火箭在飛行時段內穩定。同時，PD控制在各個時間段需要不同的靜態增益系數a0、動態增益系數a1以及多套校正網絡，魯棒性較差，對校正網絡依賴性強。采用H∞控制理論設計的控制器只需要一套校正網絡，魯棒性好，設計控制器時可不考慮彈性振動和液體晃動等高頻信號，設計簡單可靠。

4 結論

以某新型運載火箭為對象，建立發動機振動方程。考慮發動機振動可能會與全箭模態相互諧振，通過設計魯棒H∞姿態控制器，使得該運載火箭在飛行時段中穩定。同時，通過改變氣動參數以及彈性參數的取值范圍，分析PD控制器以及魯棒H∞控制器的魯棒性，驗證了本文設計的H∞控制器的強魯棒性，以及對網絡依賴性較低，提高了運載火箭姿態控制系統的穩定品質，具有一定的工程應用價值和前景。

［1］ 楊云飛，葉誠敏.基于Simulink的運載火箭姿態控制系統時域仿真軟件開發［J］.導彈與航天運載技術，2006(5):39-43.(Yang Yunfei，Yie Chengmin.Development of software for time domain simulation in attitude control system of launch vehicle based on simulink［J］.Missiles and Space Vehicles，2006(5):39-43.)

［2］ 潘忠文.運載火箭動力學建模及振型斜率預示技術［J］.中國科學 E 輯:技術科學，2009，39(3):469-473.

［3］ Kojiechnkob K C，Cyxob B H.Flexible Aerocraft as Object of Automatic Control System［M］.Beijing:National Defense Industry Press，1979:51-58.

［4］ Greensite A L.Analysis and Design of Space Vehicle Flight Control System［M］.Beijing:National Defense Industry Press，1978:161-178.

［5］ 楊云飛，陳宇，李家文，潘忠文.運載火箭搖擺發動機與全箭動力學特性耦合關系研究［J］.宇航學報，2011，32(10):2095-2102.(Yang Yunfei，Chen Yu，Li Jiawen，Pan Zhongwen.Research on the coupling between swiveled engines and dynamic characteristics of launch vehicle［J］.Journal of Astronautics，2011，32(10):2095-2102)

［6］ 譚述君，周文雅，吳志剛，楊云飛.運載火箭姿態控制系統的自適應控制設計［C］.第九屆全國動力學與控制會議手冊，2012.

［7］ 甘永梅，周鳳岐.運載火箭姿態控制系統的魯棒H∞控制與設計［J］.彈箭與制導學報，1999，2:1-8.(Gan Yongmei，Zhou Fengqi.Robust H∞Control and design of launch vehicle attitude［J］.Journal of Projectiles Rockets Missiles and Guidance，1999，2:1-8)

［8］ Wise K A，Mears B C.and Poola K.Missile autopilot design using H∞optimal control with μ synthesis［C］.Proceedings of the American Control Conference，1990，5:2362-2367.

［9］ Chen B S，Wu C S，Jan Y W.Adaptive fuzzy mixed H2/H∞attitude control of spacecraft［J］.IEEE Trans.Aerospace Electron Systems，2000，36(4):1348-1359.

［10］ 徐延萬，主編.液體彈道導彈與運載火箭系列-控制系統(上)［M］.北京:中國宇航出版社，1989:132-140.