再入飛行器試驗運載火箭彈道設計研究

徐 勤 劉 昆 雷 凱 李平岐

1.國防科學技術大學航天與材料工程學院，長沙410073

2.北京宇航系統(tǒng)工程研究所，北京100076

對于再入飛行器的試驗，運載火箭飛行試驗一般考慮 3 個因素［1-3］:

1)再入飛行器的再入模擬量及落地要求

再入飛行器再入時刻的模擬量要求，即再入飛行器再入過程的最小負加速度、平均熱流、駐點熱流、總加熱量，以及再入落點的落角、落速、再入段射程等，只與某一再入高度上的再入速度和再入傾角有關，而與再入前的飛行彈道無關，由此可以設計一種彈道，它以較小的射程實現較大射程的再入速度和再入傾角，用較小的射程模擬較大的再入環(huán)境，本文研究的低彈道就是這種彈道。

2)火箭飛行試驗的航區(qū)要求

火箭飛行試驗航區(qū)的建設及安全要求，對于試驗的首區(qū)與落區(qū)，考慮國土范圍、航區(qū)安全與地形、地貌和交通等因素，一般不能任意選擇和變動，因此考核再入飛行器所需要的試驗射程范圍，自然也受到靶場條件的限制。航區(qū)則主要考慮:再入飛行器落區(qū)的測量及試驗裝置回收問題，火箭飛行過程分離的子級殘骸落區(qū)安全性問題，飛行試驗過程中可能故障導致的箭下點飛行軌跡安全問題。

3)火箭的技術狀態(tài)

由于研制經費、進度及產品化等因素，進行低彈道試驗的運載火箭一般是在用于其他飛行試驗的運載火箭基礎上進行適應性改進而來，此時火箭的級間比、各子級的結構比、推重比、發(fā)動機比推力、發(fā)動機高空特性系數和截面氣動負荷均已確定或只能進行細小的調整。

綜上，再入飛行器試驗運載火箭進行的再入飛行低彈道試驗問題，由于再入飛行器落區(qū)限制，可以看作是典型的末端固定的最優(yōu)控制問題。該控制問題可以描述如下:

初始條件:試驗首區(qū)發(fā)射點的地理位置，如大地經度、緯度、高度。

終端條件:試驗再入飛行器落點的地理位置，如大地經度、緯度、高度。

約束條件:1)再入飛行器再入點的再入速度、當地彈道傾角等要求;2)火箭的級間比以及各子級的結構比、推重比、發(fā)動機比推力、發(fā)動機高空特性系數、截面氣動負荷。

控制條件:火箭各子級發(fā)動機的工作時間，以及具有大、小推力發(fā)動機的子級工作組合。

1 彈道實現模式分析

再入飛行器試驗運載火箭的低彈道與一般彈道導彈的主動段彈道雖有很多相同之處，但也存在一些明顯差別，在理想情況下，可以明顯地看出兩者任務的不同帶來的差別，理想情況下，火箭只受距離平方反比中心引力場的引力作用，并假定火箭發(fā)動機按瞬時沖量方式工作。

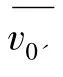
圖1 遠程火箭彈道

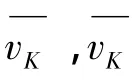
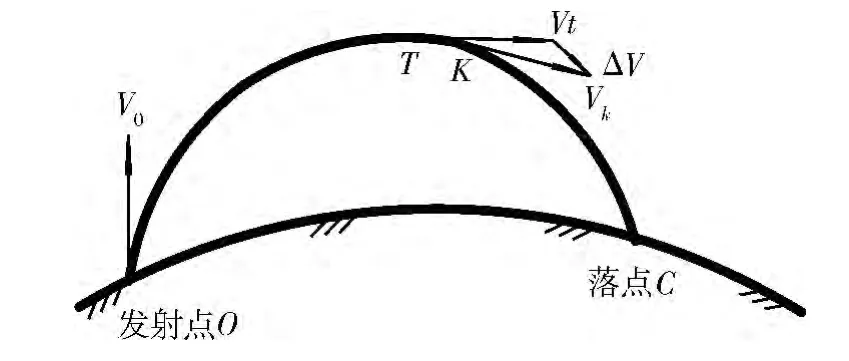
圖2 試驗彈道

由于火箭發(fā)動機大小是有限的，實際上不可能按照沖量方式工作，因此對于一般彈道式遠程運載火箭主動段彈道而言，多級火箭的發(fā)動機一級接著一級連續(xù)工作的方式實際上是能夠實現的“一次沖量”方式。

而對于再入飛行器試驗運載火箭的低彈道而言，至少要2次沖量才能完成任務，因此實際上運載火箭有2種工作模式:

1)模式I，火箭基礎級發(fā)動機在發(fā)射點附近工作一段時間，起“第1次沖量”的作用，接著完成火箭級間分離，分離后的上面級沿轉移彈道向K點滑行，在到達K點之前，火箭上面級啟動發(fā)動機，使發(fā)動機工作一段時間，起“第2次沖量”的作用，在再入飛行器進入預定彈道時，上面級發(fā)動機關機，這一模式的特點是在兩段動力飛行之間有一個自由滑行段。

對于模式I，某三級狀態(tài)運載火箭，一、二級上升飛行，然后進入滑行段，三級及再入飛行器在地球引力作用下完成彈道轉彎，三級在合適的地方進行推力矢量控制，滿足再入速度和再入傾角要求。對于此種狀態(tài)火箭，由于一、二、三級推進劑質量、發(fā)動機流量不變，故一、二、三級工作時間基本不變，而由于二、三級之間增加了滑行段，此外三級的推力矢量方向可與其啟動時刻的再入速度、再入飛行器要求的再入速度進行優(yōu)化，故射程設計有一定的調整量。此種狀態(tài)火箭三級負責最終的推力矢量控制且火箭處于下降段完成，下降段速度較之前階段較快，三級在下降段允許工作時間較短，為滿足再入速度的加速要求，要求三級工作期間的加速度較高，故三級工作時的火箭推重比較大。

2)模式Ⅱ，火箭基礎級發(fā)動機在發(fā)射點附近工作一段時間，起“第1次沖量”的作用，接著完成火箭級間分離，分離后的上面級立刻啟動發(fā)動機，并一直工作到K點附近，起“第2次沖量”的作用，在再入飛行器進入預定彈道時，上面級發(fā)動機關機，這一模式的特點是在兩段動力飛行之間沒有自由滑行段，“第1次沖量”和“第2次沖量”是連續(xù)施加的，中間沒有過渡。

對于模式Ⅱ:某二級狀態(tài)運載火箭，一級上升飛行，二級飛行負責程序轉彎并滿足再入速度、再入傾角要求。對于此種狀態(tài)火箭，由于一、二級推進劑質量、發(fā)動機流量不變，故一、二級工作時間基本不變，又由于射程與一、二級工作時間直接相關，故射程彈道設計調整余量不大。此種狀態(tài)火箭二級工作負責轉彎、加速要求，二級工作段末期火箭推重比較大，飛行過載較大。

2 彈道特征速度分析

當采用不同的轉移彈道時，若N-1級子火箭推進劑耗盡，而V仍未達到要求的vch，則由N級子火箭工作，使V增加，而V將隨ΔmN的增加而單調增加，當vch為最小值時，V亦為最小值，ΔmN也是最小值，因此，vch為最小值的彈道即是能量消耗最少的彈道。

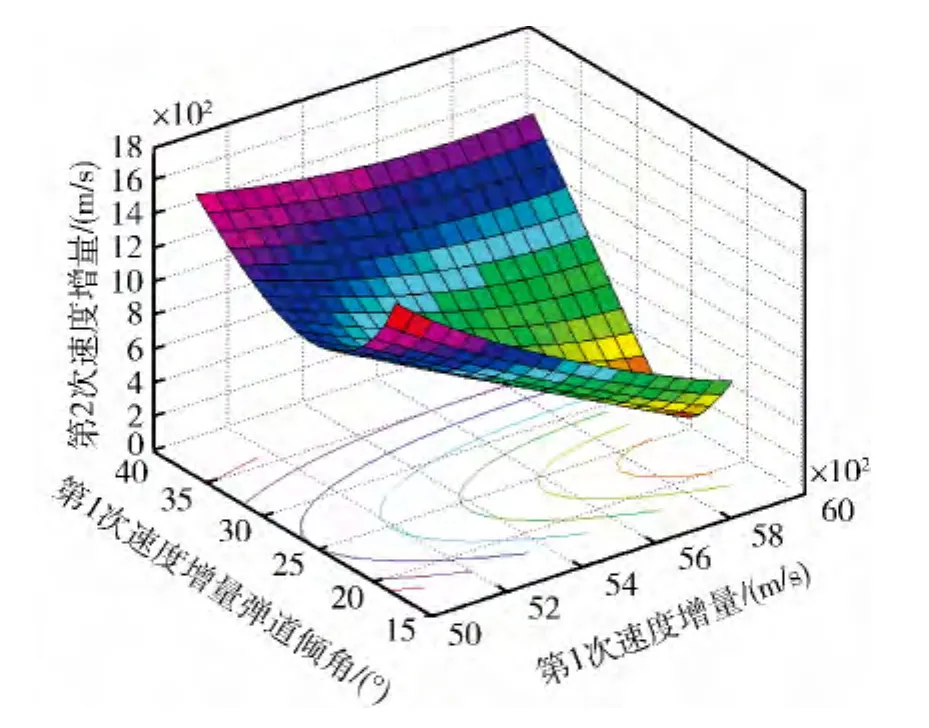
圖3 第2次速度增量需求

根據圖3和4的設計仿真數據，為了實現相同的再入速度和再入傾角要求，通過火箭控制系統(tǒng)優(yōu)化選擇第1次速度增量的大小以及彈道傾角，可將總速度增量vch需求降低至最小。

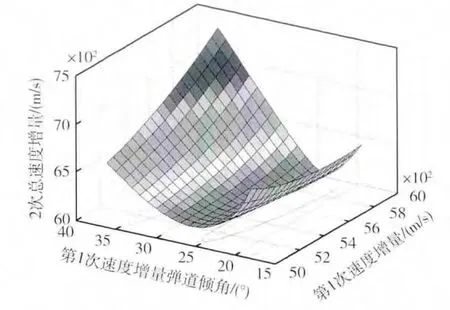
圖4 2次總速度增量需求

3 “第2次沖量”彈道實現研究

“第2次沖量”的彈道實現，即施加段主要解決如下問題［6］:

1)開始施加點的位置選擇，為了保證再入參數的精度要求及最終落點的目標點要求，在彈道設計時必須通過迭代的方法選擇合適的施加點位置;

2)施加參數的選擇，包括火箭發(fā)動機的推力大小、方向和工作時間;

3)施加段火箭的制導設計，以及火箭發(fā)動機關機方程的建立，并考慮在實際有干擾的情況下如何確定發(fā)動機的關機。

“第2次沖量”施加段火箭發(fā)動機的關機方案問題，因其再入飛行器分離后的再入段不控制，直接影響再入參數的模擬和最終落點的精度，下面只討論火箭發(fā)動機4種主要的關機方案:

(1)按時間關機方案

當設計標準施加段彈道得到的標準關機時間tkn作為施加段火箭發(fā)動機的關機時間，則有:

當前時刻等于關機時間的時候，即Δtk=0火箭發(fā)動機停止工作。按時間關機方案的優(yōu)點在于當火箭制導系統(tǒng)不能正常工作時，仍能確定關機時刻，因此一般按時間關機作為備保的關機方案。

(2)按增益速度關機

設標準關機點的增益速度為vgn(tkn)，則有:

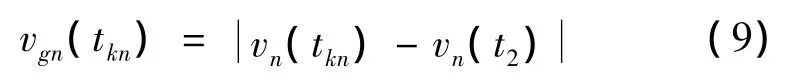
其中，vn(t2)為標準彈道“第2次沖量”施加起始點的速度值，vn(tkn)為標準關機速度值。

在實際飛行施加段過程的某一時刻，火箭的速度值為v，則火箭的實際增益速度值為vg(t)。

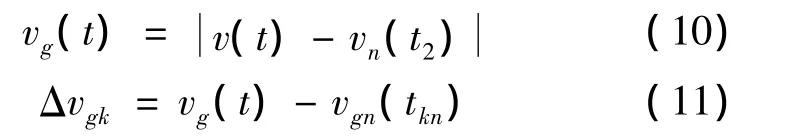
當Δvgk=0時，火箭發(fā)動機停止工作。按增益速度關機方案，再入飛行器再入模擬要求及最終落點的精度均高于按時間關機方案，此關機方案簡單易行。

(3)按再入速度傾角關機方案

選擇反映施加段火箭發(fā)動機關機點飛行狀態(tài)參數變化的速度傾角Θk作為火箭發(fā)動機關機特征的關機方案。火箭速度傾角Θk可表示為火箭“第2次沖量”施加段結束點，及發(fā)動機關機點飛行狀態(tài)的函數。

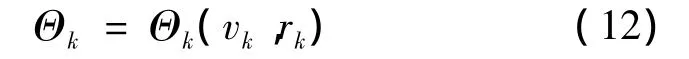
其中:vk，rk分別為火箭發(fā)動機關機點的速度值和地心距離。

在一階攝動條件下，發(fā)動機關機點當地速度傾角偏差ΔΘC可表示為:

當J(t)=Jn(tkn)時，關閉火箭發(fā)動機，仿真分析表明，該關機方案能較好地滿足再入飛行器再入模擬量的要求。

(4)按試驗射程關機方案

射程控制的目標函數是落點偏差為0，即實際飛行射程Lk等于理論彈道計算的標準射程Lkn。射程是飛行彈道參數和時間的函數。

采用射程關機方案，火箭飛行過程中需要連續(xù)測算火箭的速度、位置，并利用這些參數采用解析或數值計算方法求解制導方程，形成制導信號進行制導，同時預測射程偏差，當ΔL=0時實施發(fā)動機關機。

4 結論

1)再入飛行器試驗火箭的彈道設計一般考慮飛行器的再入模擬量及落地要求、火箭飛行試驗的航區(qū)要求、火箭的技術狀態(tài)等3個主要因素，且是典型的末端固定的最優(yōu)控制問題;

2)火箭在理想情況下，最少要施加2次沖量才能完成再入任務要求，第1次沖量在發(fā)射點施加，第2次沖量使有效載荷獲得再入模擬要求并進入預定彈道;

3)第2次沖量確定條件下，火箭再入飛行試驗需要的特征速度僅與火箭基礎級的飛行速度、當地彈道傾角以及再入飛行器再入點的飛行速度與當地彈道傾角有關;

4)第2次沖量的彈道實現，即施加段主要解決施加點位置選擇、施加參數選擇和施加段火箭制導設計等問題，其中對于火箭發(fā)動機關機方程，一般有按時間、按增益速度、按再入速度傾角和按試驗射程4種主要關機方案。

［1］ Bruce A Smith.Second MX Flight［C］.Design Ground Test Data:A/W，1983.

［2］ Browning S C，MX Stage III.A review of the design entering full scale engineering development［J］.AIAA 80-1186.

［3］ 薛成位，主編.彈道導彈工程［M］.北京:中國宇航出版社，2002.

［4］ 賈沛然，等.遠程火箭彈道學［M］.長沙:國防科技大學出版社，1993.

［5］ 任萱.人造地球衛(wèi)星軌道力學［M］.長沙:國防科技大學出版社，1988.

［6］ 趙漢元.飛行器再入動力學與制導［M］.長沙:國防科技大學出版社，1997.