輪式移動機器人定點目標控制問題及線性分解方法?
宿 浩, 唐麗娜, 唐功友
(中國海洋大學信息科學與工程學院,山東 青島 266100)
?
輪式移動機器人定點目標控制問題及線性分解方法?
宿 浩, 唐麗娜, 唐功友
(中國海洋大學信息科學與工程學院,山東 青島 266100)
提出輪式移動機器人在給定時間內的定點目標控制問題并提出一種解決該類問題的線性分解控制方法。根據輪式移動機器人的非完整性非線性動力學模型的結構特性,將機器人的運動分解為原地旋轉和直線運動。按不同時間段分別設計移動機器人的原地旋轉和直線運動規律,從而實現了非線性系統的線性解耦分解。利用線性分解控制方法,將輪式移動機器人的原地旋轉和直線運動按勻加速起步、勻速行駛和勻減速停車運動規律控制,實現了在給定時間內的定點目標控制。仿真結果驗證了所提出方法的有效性。
移動機器人;非線性系統;定點目標控制;線性分解;解耦
輪式移動機器人位置控制問題是移動機器人控制的基本問題。近年來,國際上關于位置控制問題的主要研究成果為點鎮定研究,提出了若干解決移動機器人點鎮定控制的方法。例如文獻[1]利用反饋線性化實現輪式移動機器人獨立驅動的點鎮定控制;文獻[2]提出了一種兩輪輪式機器人點鎮定的分段比例智能控制、文獻[3]利用分段連續控制律保證了非完整移動機器人位置逐步收斂于期望的目標,并保證了閉環系統的指數穩定性;針對非完整運動學系統的不確定模型,文獻[4]提出了一種動態反饋控制律,使得移動機器人的姿勢和方向收斂到期望值,并證明了系統的魯棒穩定性;利用蟻群優化算法,文獻[5]提出了一種具有四個獨立驅動車輪的四輪移動機器人全方位智能運動控制器;對一類具有飽和輸入的非完整運動約束的移動機器人,文獻[6]提出了半全局實用鎮定控制方案;文獻[7]通過使用高階的擴展,控制移動機器人的速度和方向,控制策略保證了移動機器人能漸近收斂到給定的目標點和運動軌跡;針對模型的質心與幾何中心不重合的情況,文獻[8]利用時變連續控制律解決了移動機器人的鎮定控制問題,并且利用自適應技術解決了兩者之間距離未知時的鎮定控制問題。
點鎮定問題是當時間t→∞時,使移動機器人無限接近于預先給定的位置。然而,在實際問題中,我們往往希望在有限時間內。針對這一問題,文獻[9]研究了非線性參數化系統的自適應有限時間鎮定問題,并設計了能保證系統狀態全局有限時間收斂到原點的控制算法;文獻[10]針對移動機器人定點目標控制問題提出了一種非線性系統的線性分解方法,實現了在給定的有限時間內機器人到達原點的控制算法;文獻[11]將控制目標拓寬到了給定停車區域,并設計了有限時間的控制律。
然而,文獻[10-11]僅針對移動機器人運動學模型設計定點目標控制算法,而沒有考慮移動機器人動力學特性在實際系統中的實現問題。本文針對輪式移動機器人位置控制的需求提出輪式移動機器人在給定時間內的定點目標控制問題,并根據針對移動機器人的動力學模型提出一種解決定點目標控制問題線性分解控制方法。首先根據輪式移動機器人的非完整性非線性動力學模型的結構特性,將機器人的運動分解為原地旋轉和直線運動。然后按不同時間段分別設計了移動機器人的原地旋轉速度和直線運動速度控制策略,從而實現了非線性系統的線性解耦分解。利用線性分解控制方法,將輪式移動機器人的原地旋轉和直線運動按勻加速起步、勻速行駛和勻減速停車運動規律控制,實現了在給定時間內的定點目標控制。
1 問題描述
輪式移動機器人通過調節速度和航向實現從某一原始位置到給定目標位置的控制目的。假設移動機器人的位置用笛卡爾直角坐標系描述(見圖1)。機器人狀態由其質心在坐標系下的位置及姿態(即航向)來表示。
機器人當前位置由直角坐標(x(t),y(t))表示,機器人當前的姿態用前進方向和x軸正方向的夾角θ(t)
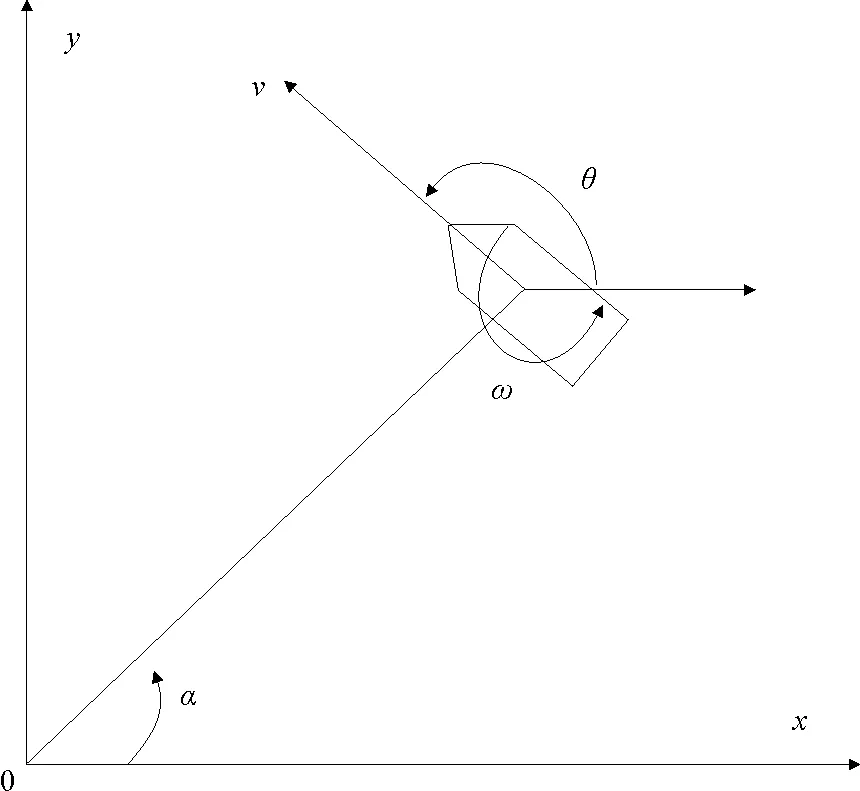
圖1 移動機器人的位置和姿態坐標
(即航向角坐標)表示。令v(t)和ω(t)分別表示機器人當前的線速度和角速度。并假設線速度v(t)和角速度ω(t)是獨立的,即線速度v(t)和角速度ω(t)分別由兩個電動機單獨驅動。這一假設說明,移動機器人可以在運動中可以原地轉圈。
令α(t)為當前機器人質心位置與x軸正方向的夾角。不失一般性,在本文中我們只討論機器人在(x,y)坐標系的第一象限中。從而有0≤α(t)≤π/2,令航向角-π+α≤θ(t)≤π+α。
如圖1所示的移動機器人的運動學方程可以描述為:
(1)
由牛頓第二定律易知,機器人動力學方程可以描述為:
(2)
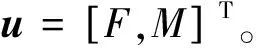
f(v)=cvv(t),
g(ω)=cωω(t)。
(3)
其中cv和cω是已知的阻尼系數。將(3)帶入(2),得到
(4)
由系統(1)知,滿足約束條件
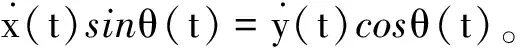
(5)
從系統模型(1),(4)和(5)知,移動機器人的位置和運動軌跡控制是一類非完整性非線性系統。我們知道,通常非完整性非線性系統的控制策略設計問題是較難解決的研究課題。
2 線性分解控制策略
本文根據系統模型(1),(4)和(5)的特點,提出一種線性分解控制策略。線性分解控制策略的思路是將n階系統的n個狀態變量按順序分解為N(N≤n)組,按分組順序將控制過程分為N個階段完成控制任務,在每個階段完成一組狀態變量的控制。從而實現非線性系統的線性解耦控制。
首先將系統(1),(4)分解為2個子系統。為此,令
(6)
則系統(1),(4)可以由以下2個子系統描述:
(7)
其中:
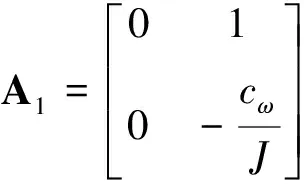

(8)
由(7)可知,子系統∑1是線性定常系統,其響應對子系統∑2有影響,但不受子系統∑2的影響。而子系統∑2是一個放射非線性系統,其非線性系數矩陣A2(z1)僅與θ(t)有關。
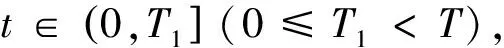
(9)
其中α0=α(0),定義
(10)
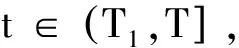
經過以上線性分解控制策略,將一個非線性控制系統分解為兩個線性定常系統。
3 定點目標控制律設計
現在,研究經線性分解后的2個線性定常子系統(7)的控制律設計問題。
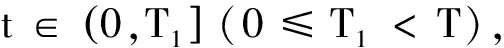
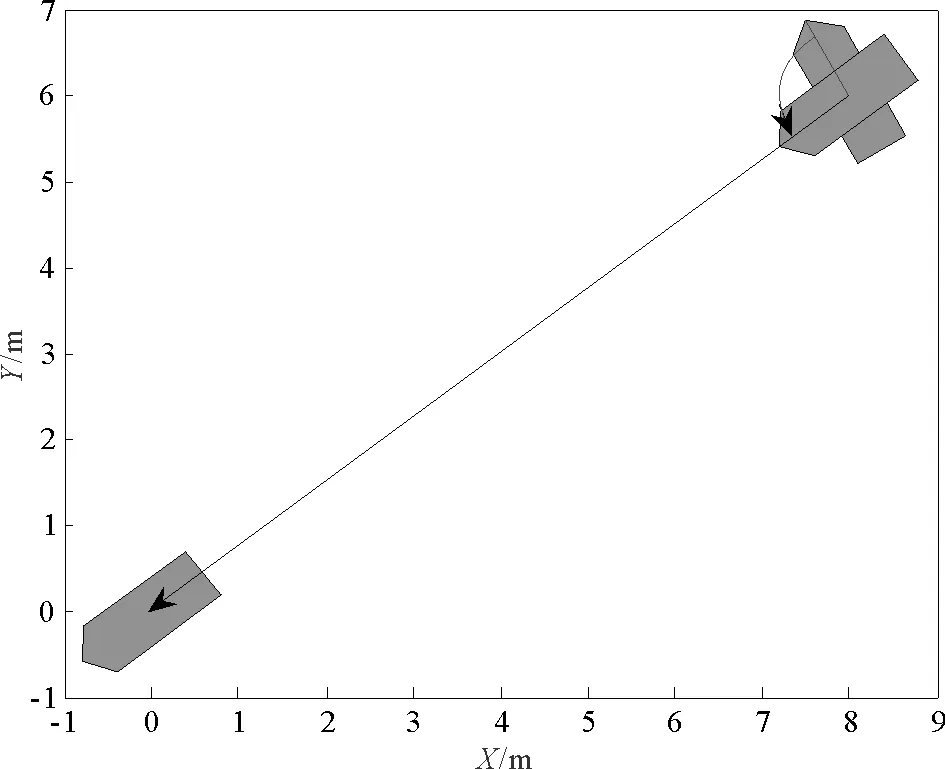
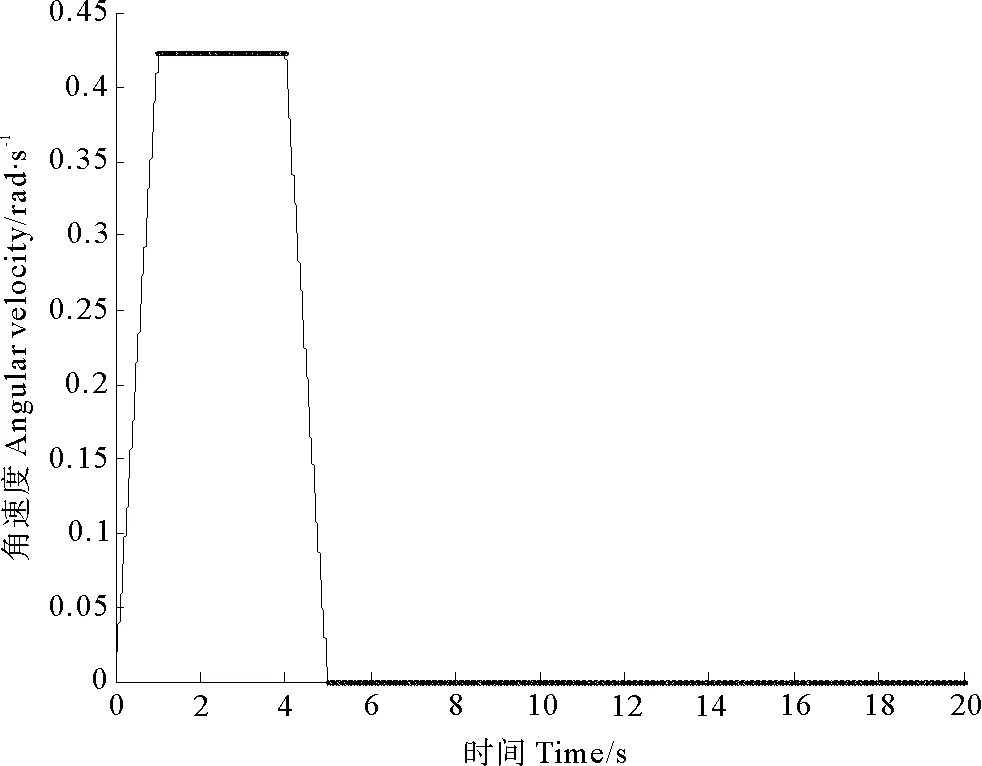
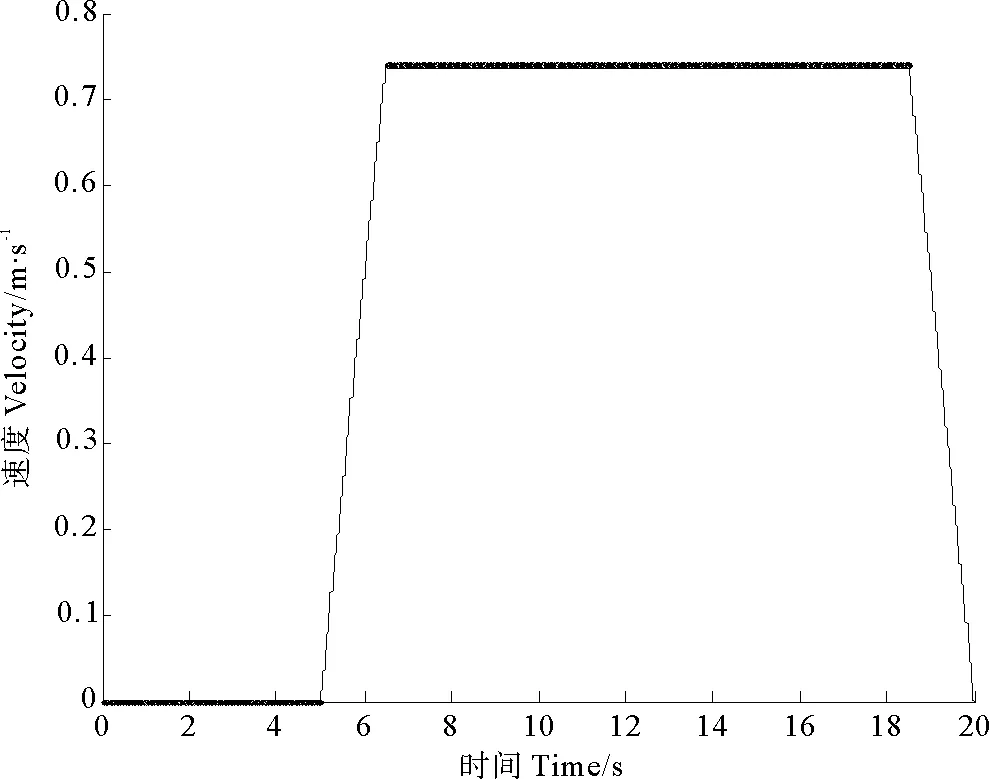
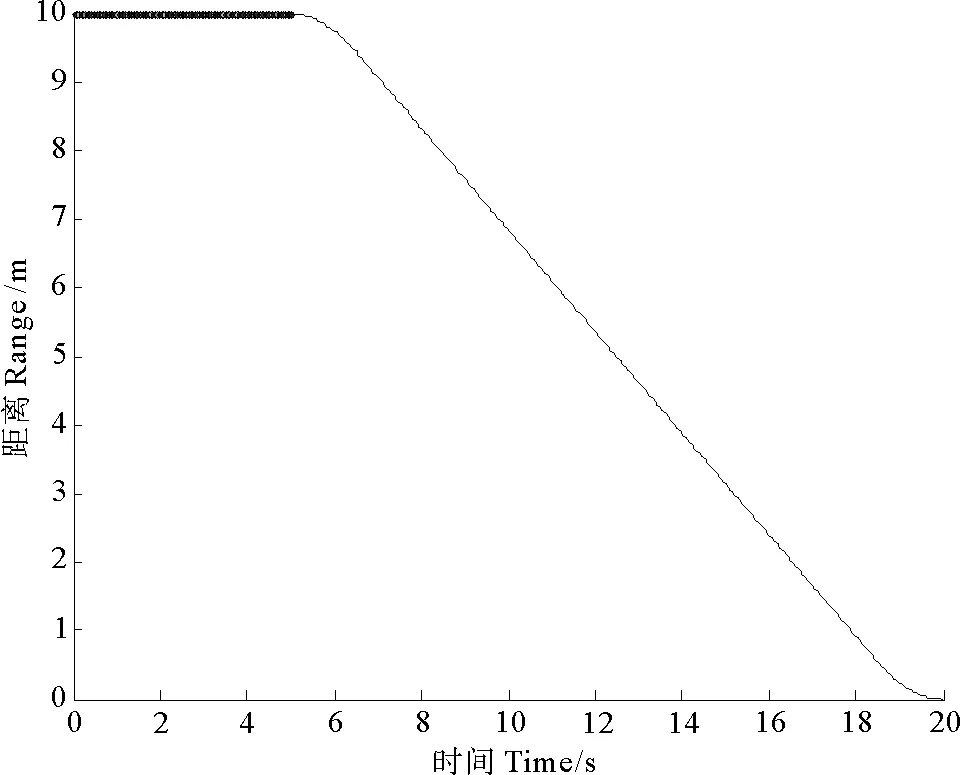
F(t)=0, 0 (11) 證明 在非線性系統(7)中,先考慮子系統∑1。將(11)代入子系統∑1的第2個方程,得到 (12) (12)的解表達式為 (13) 再將(13)代入子系統∑1的第一個方程,得到 (14) (14)的解表達式為 (15) 由(13)和(15)得到: ω(T1)=0, θ(T1)=α0+πsgn+(θ0-α0)。 即(9)成立。再考慮子系統∑2。將F(t)=0代入子系統∑2的第2個方程,得到: 從而有z2(t)=z2(0)(0 假設已經按定理1設計的控制律,在時刻T1將系統的狀態轉移至 (16) M(t)=0, T1 (17) 則z2(T)=0成立。 θ(T1)=α0+πsgn+(θ0-α0);ω(T1)=0。 (18) (12)的解表達式為 θ(t)=α0+πsgn+(θ0-α0); ω(t)=0;T1 (19) 再考慮子系統∑2。將(17)代入子系統∑2的第3個方程并由(16),得到: (20) (20)的解表達式為 (21) (22) 及約束條件 (23) 令 (24) 并注意到 (25) 由(16),(21),(22),(23),(24)和(25)得到 (26) (26)的解表達式為 (27) 由(21)和(27)得到: v(T)=0, x(T)=0, y(T)=0。 即 從而有z2(t)=z2(0)(0 綜合(11)和(17),得到移動機器人的定點控制律: (28) 和 (29) 為驗證所提出方法的有效性,基于Matlab編寫程序進行仿真。以一個兩輪移動機器人為研究對象,其質量m=30 kg,轉動慣量J=15 kg·m2,阻尼系數cv=20 kg·s-1和cω=10 kg·m2·s-1。為了驗證定點目標控制律(24)和(25)的有效性,選取起始位姿為 要求 控制律(24)和(25)分別將移動機器人的運動分解為原地旋轉運動和直線運動,示意圖見圖2。 該點到原點的鎮定仿真如圖3~6所示.如圖3為移動機器人的角速度曲線;圖4為移動機器人的直線運動速度曲線;圖5為移動機器人的航向角曲線;圖6表示移動機器人的位置曲線. 由圖3可知,機器人在5.0s時鎮定,此刻位姿收斂到零。由圖4~6可看出,速度、角速度和力矩起始為零,而且最終收斂到零. 圖2 移動機器人的運動分解 圖3 移動機器人的角速度曲線 圖4 移動機器人的直線運動速度曲線 圖5 移動機器人的航向角曲線 圖6 移動機器人的位置曲線 本文針對移動機器人的定點目標控制問題,提出一種線性分解方法。線性分解方法在時間上將具有非完整約束移動機器人模型分解為兩個線性系統,實現了非線性系統的線性解耦分解。利用線性分解方法簡化了移動機器人的定點目標控制設計,實現了移動機器人的有限時間定點目標控制。 [1] Sun S, Cui P. Path tracking and a practical point stabilization of mobile robot[J]. Robotics and Computer-Integrated Manufacturing, 2004, 20(1): 29-34. [2] 王牛, 李祖樞.一種兩輪輪式機器人點鎮定智能控制實現 [J]. 控制理論與應用, 2010, 17(4): 437-443. [3] Farzad P. Exponential stabilization of nonholonomic mobile robots [J]. Computers and Electrical Engineering, 2002, 28(5): 349-359. [4] Wang C, Liang Z, Jia Q. Dynamic feedback robust stabilization of nonholonomic mobile robots based on visual servoing [J]. Journal of Control Theory and Applications, 2010, 8(2): 139-144. [5] Huang H C. Intelligent motion control for four-wheeled omnidirectional mobile robots using ant colony optimization [J]. Next Wave in Robotics: Communications in Computer and Information Science, 2011, 212: 94-106. [6] Wang C. Semiglobal practical stabilization of nonholonomic wheeled mobile robots with saturated inputs[J]. Automatica, 2008, 44(3): 816-822. [7] Buccieri D, Mullhaupt P, Jiang Z P, et al. Velocity-scheduling control for a unicycle mobile robot: Theory and experiments [J]. IEEE Transactions on Robotics, 2009, 25(2): 451-458. [8] 李勝, 馬國梁, 胡維禮. 一類不確定非完整移動機器人的時變自適應鎮定 [J]. 機器人, 2005, 27(1): 10-13. [9] Gao F, Shang Y, Yuan F. Robust adaptive finite-time stabilization of nonlinearly parameterized nonholonomic systems [J]. Acta Applicandae Mathematicae, 2013, 123(1): 157-173. [10] 唐麗娜, 宿浩, 郭忠文. 移動機器人定點目標控制的線性分解方法 [J]. 中國海洋大學學報(自然科學版), 2013, 44(11):114-117. [11] 楊雪, 唐功友, 蓋紹婷. 自主式智能體有限時間停車問題及控制策略設計 [J]. 控制與決策, 2013, 28(6): 953-956. 責任編輯 陳呈超 Position Target Control and Linear Decomposition Approach for Wheeled Mobile Robots SU Hao, TANG Li-Na, TANG Gong-You (College of Information Science and Engineering, Ocean University of China, Qingdao 266100, China) The problem of position target control in a given period of time for wheeled mobile robots is presented. A linear decomposition approach to solve this kind of problem is proposed. According to the structural characteristics of the nonholonomic nonlinear dynamic model of the wheeled mobile robot, the robot motion can be decomposed into in-situ rotary and rectilinear motion. The in-situ rotary and rectilinear motion law of the mobile robot are designed respectively, which realizes the decoupling decomposition of the nonlinear system. Using the linear decomposition control approach, in-situ rotary and rectilinear motion for wheeled mobile robot are designed as uniformly accelerated starting, uniformly moving and uniform deceleration parking processes, to achieve the position target control in a given period of time. Simulation results verify the effectiveness of the proposed method. mobile robot; nonlinear systems; position target control; linear decomposition; decoupling 國家自然科學基金項目(61074092);山東省自然科學基金項目(ZR2010FM019)資助 2013-11-09; 2014-05-20 宿 浩(1982-),男,博士生。E-mail: asfreedom@163.com P13 A 1672-5174(2015)09-116-06 10.16441/j.cnki.hdxb.20130414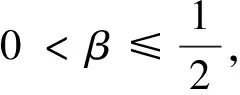
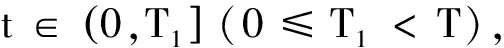
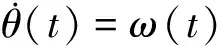
4 實例仿真

5 結語

