基于灰色預測滑?？刂频聂敯麸w行控制器設計

焦鑫, 江駒, 孟宏鵬

(南京航空航天大學 自動化學院, 江蘇 南京 210016)

基于灰色預測滑模控制的魯棒飛行控制器設計

焦鑫, 江駒, 孟宏鵬

(南京航空航天大學 自動化學院, 江蘇 南京 210016)

為了解決近空間可變翼飛行器大包絡飛行以及小翼伸縮過程中受到不確定性參數和未知外部干擾的問題,第一次將灰色理論引入飛行控制領域。首先對飛行器的非線性模型不確定性參數進行分析,利用灰色GM(0,N)模型精確預測不確定性參數和外部干擾;然后根據所預測的數值,設計了基于灰色預測滑?？刂频聂敯麸w行器,從而有效補償不確定性參數和外部干擾對飛行器的影響。仿真結果表明,灰色GM(0,N)模型能夠有效預測不確定性參數和未知外部干擾,并通過所設計的飛行控制器補償其影響,保證了飛行器的穩定性和魯棒性。

灰色預測; GM(0,N)模型; 近空間可變翼飛行器; 飛行控制器

0 引言

近空間可變翼飛行器具有強時變、非線性、強耦合以及不確定性等特點[1],尤其是模型參數的不確定性,使飛行控制難度增大。

針對以上問題,目前已有不少學者進行了較為深入的研究。具有魯棒性的反饋線性化可以用來提供一種針對吸氣式近空間可變翼飛行器在模型不確定和飛行條件不斷變化情況下速度和高度跟蹤的方法[2]。文獻[3]將非線性閉環回路與自適應動態逆相結合,為吸氣式近空間可變翼飛行器設計了一個非線性魯棒自適應飛行控制器。文獻[4-5]將終端滑模與二階滑?？刂葡嘟Y合,設計了飛行控制器,用來解決近空間可變翼飛行器參數不確定問題。線性參數變化法也被用于近空間飛行器的飛行控制器設計[6]。雖然以上提到的這些方法都能在一定程度上克服參數不確定對近空間飛行器的影響,但這些方法都需要對非線性模型進行一定的簡化，或者忽略一部分不確定性參數和外部干擾的影響,這些都會對工程實現帶來較大的影響。

灰色預測針對不確定信息具有很好的預測效果,目前已廣泛用于能源消耗、經濟發展、社會變化以及行為趨勢等方面[7-8],在越來越廣泛的領域發揮其重要作用。近年來,灰色預測已經逐漸被用于控制工程領域[9-10]。

本文通過GM(0,N)模型來精確預測模型中不確定參數和外部干擾的數值,不論其大小。同時,對由于不確定參數和外部干擾對飛行器所造成的影響進行補償,從而能夠使飛行器精確跟蹤理想指令信號,以保證飛行控制器的控制效果。

1 近空間可變翼飛行器模型

根據力和力矩平衡,可建立近空間可變翼飛行器縱向模型[11]:

(1)

(2)

(3)

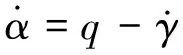
(4)

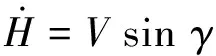
(5)

(6)

參數不確定性主要體現在模型參數和氣動參數的不確定。本文中,不確定參數作為外加變量加入正常變量中用于控制器設計。主要參數如下:

m=m0(1+Δm),Iy=Iy0(1+ΔIy),s=s0(1+Δs)

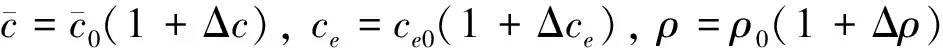
(7)

其中:

(8)

(9)

(10)

(11)

(12)

Lαcosγ-Dαsinγ]

(13)

式中:Dα=?D/?α,Lα=?L/?α,Cβ=?CT/?β。其他各參數的含義見文獻[11]。

2 控制器設計

2.1 系統整體結構

近空間飛行器的模型參數具有不確定性,同時,飛行器在近空間中飛行,由于飛行環境復雜,會受到很多未知的外部干擾。本文將設計基于灰色預測滑模控制的近空間可變翼飛行器的魯棒飛行控制器,系統結構框圖如圖1所示。

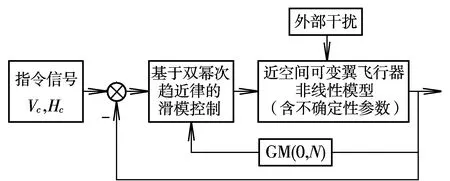
圖1 系統結構框圖Fig.1 The system structure digram

圖1中,考慮到近空間可變翼飛行器的非線性模型中存在參數不確定性,所以只用滑?？刂撇荒軡M足具有不確定性系統的控制需求。在只用滑?？刂破鞯牟环€定控制系統中,不確定參數和外部干擾值通過GM(0,N)模型進行預測[13],然后根據預測的數值,所設計的基于灰色預測滑?？刂频聂敯艨刂坡蓪a償不確定性和外部干擾對飛行器的影響,從而使系統保持精確跟蹤理想指令信號的性能。

2.2 基于雙冪次趨近律的滑?？刂?/p>

設跟蹤誤差為:eV(t)=V(t)-Vd(t),eH(t)=H(t)-Hd(t)。定義積分滑模面:

(14)

式中:λV,λH為正常數;積分項用于消除穩態誤差。sV和sH對時間t的一階導數為:

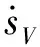
(15)

設計雙冪次趨近律:

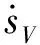
(16)

式中:kV1,kV2,kH1,kH2>0;αV>0,αH<1;βV,βH>1。

根據式(7)、式(15)和式(16)可以得到如下控制律:

(17)

2.3 模型不確定性分析

在近空間飛行器反饋線性化的模型式(7)中,參數b11,b12,b21,b22都是不確定的。因飛行器模型中參數是不確定的,這就意味著近空間可變翼飛行器的非線性模型是一個灰色系統,所以不能準確地算出近空間可變翼飛行器系統模型的具體數值。

(18)

進一步,因為飛行器所受外部干擾也是不確定的,測量誤差是不可避免的,也就是說,式(7)的矩陣[fV,fH]T也是不確定的,記為[fV′,fH′]T。

(19)

所以,式(7)則相應地變為:

(20)

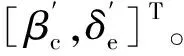
2.4 灰色GM(0,N)模型

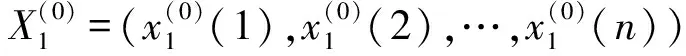
(21)

(22)

?

(23)

為GM(0,N)模型[14]。

GM(0,N)模型不含導數,因此為靜態模型。GM(0,N)的建?；A是原始 1-AGO序列。

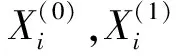
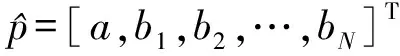
2.5 控制器設計

當系統具有不確定和受到外部干擾時,傳統的滑?？刂坡墒?17)已不能保證近空間可變翼飛行器非線性系統的穩定性。為了補償不確定部分對飛行器的影響,需要對不確定性參數和外部干擾值進行預測。根據式(7)、式(15)和式(20),相應的sV和sH的導數可以重新寫為:

(24)

如果仍然使用未加處理的βc和δe控制信號時,展開式(20),可以得到:

(25)

下面通過灰色GM(0,N)模型來預測不確定性和外部干擾。

第一步:將式(25)離散化:

(26)

式中:t=kT,T為采樣時間;x1=b11βc;x2=b12δe;x3=b21βc;x4=b22δe;X1=[x1,x2];X2=[x3,x4]。

第二步:分別建立x1,x2,x3,x4和D1,D2的原始離散序列:

(27)

式中:N=5。

第三步:建立x1,x2,x3,x4和D1,D2的1-AGO離散序列:

(28)

其中:

第四步:計算下式:

(29)

(30)

第五步:計算不確定性參數和外部干擾值:

根據式(25)可以得到:

(31)

(32)

不確定性參數和外部干擾可以通過下式所示的最小二乘方法計算出來:

(33)

(34)

第六步:設計基于灰色預測滑模控制的魯棒控制律。

根據式(20),可以得到基于灰色預測的魯棒控制器來補償不確定性參數和外部干擾對近空間飛行器的影響。

(35)

3 仿真驗證

為了更好地驗證所述控制器的效果,本文將考慮不確定性參數和未知外部干擾影響同時存在的情況。

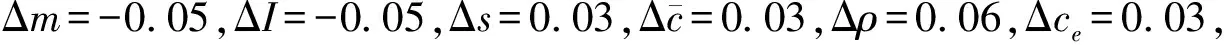
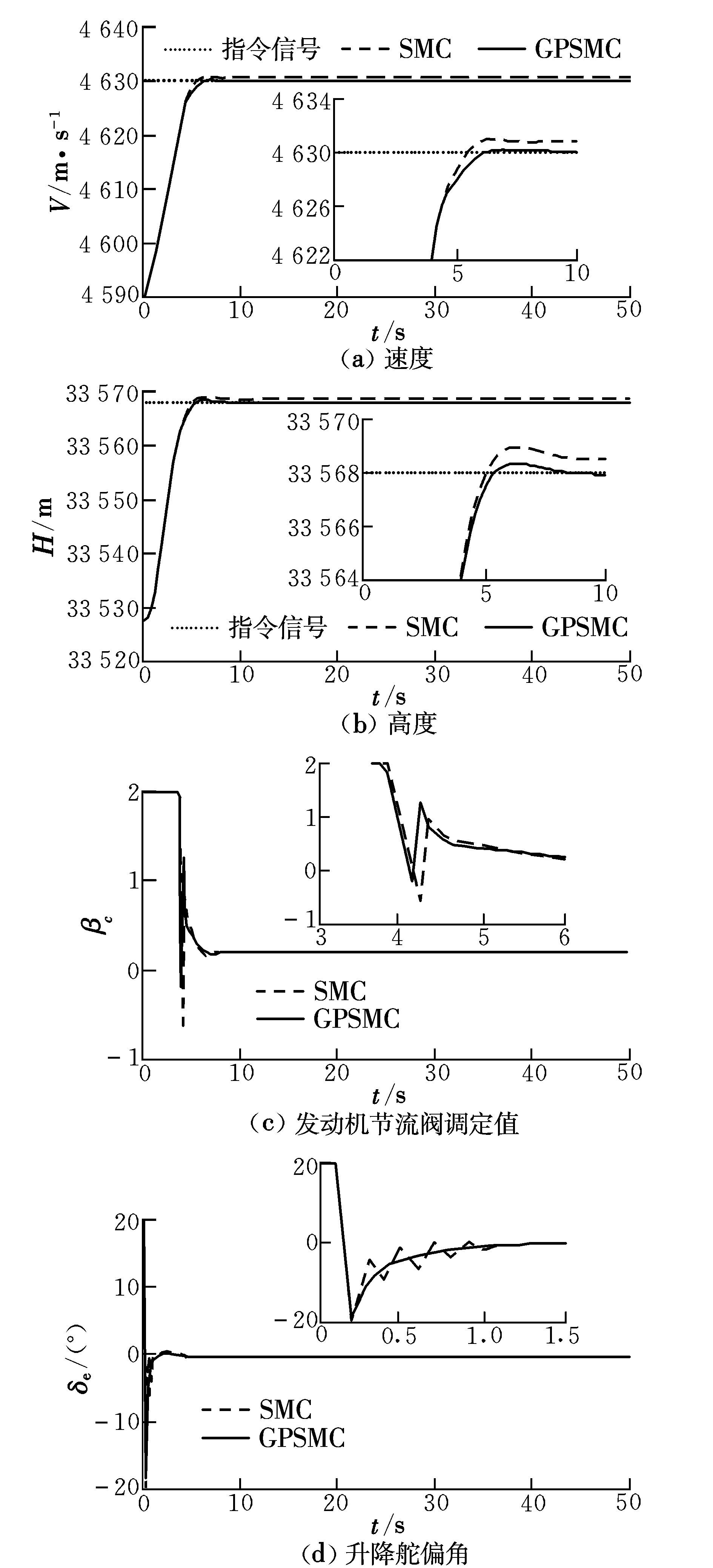
圖2 系統控制效果Fig.2 Control effects of the system

圖2中,GPSMC表示灰色預測滑?？刂?SMC表示滑模控制?？梢钥闯?滑?？刂破鞔嬖谝欢ǖ姆€態誤差,不能有效地控制系統;而基于灰色預測滑?？刂频娘w行控制器可以精確預測系統模型中所存在的不確定性參數的值,并完全進行補償,使近空間可變翼飛行器能夠精確跟蹤指令信號,保證了系統的穩定性和魯棒性。

4 結束語

本文將灰色理論應用于飛行控制領域,設計了基于灰色預測滑模控制的飛行控制器。通過灰色GM(0,N)模型將系統中的不確定性參數和未知外部干擾預測出來,再根據所預測出的值,設計魯棒控制器。該控制器能使近空間可變翼飛行器精確跟蹤指令信號,保證了系統的穩定性和魯棒性。本文對研究近空間飛行器的飛控系統具有一定的理論價值和參考意義。為了增強實際應用價值,本課題將在后續研究中加入自適應控制的思想。

[1] 孫長銀,穆朝絮,余瑤.近空間高超聲速飛行器控制的幾個科學問題研究[J].自動化學報,2013,39(11):1901-1913.

[2] Yurkovich S,Sigthorsson D O,Jankovsky P,et al.Robust linear output feedback control of an airbreathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1052-1066.

[3] Fiorentini L,Serrani A,Bolender M A,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles [J].Journal of Guidance,Control,and Dynamics,2009,32(2):402-417.

[4] Zhang R,Sun C,Zhang J,et al.Second-order terminal sliding mode control for hypersonic vehicle in cruising flight with sliding mode disturbance observer[J].Journal of Control Theory and Appllication,2013,11(2):299-305.

[5] 宗群,蘇芮,王婕,等.高超聲速飛行器自適應高階終端滑?？刂芠J].天津大學學報(自然科學與工程技術版),2014,47(11):1031-1037.

[6] 黃廣.高超聲速飛行器殘差自調節高精度控制算法研究[D].哈爾濱:哈爾濱工業大學,2013.

[7] 劉思峰,謝乃明.灰色系統理論及其應用[M].北京:科學出版社,2008.

[8] 崔立志.灰色預測技術及其應用研究[D].南京:南京航空航天大學,2010.

[9] 祝華遠,崔亞君,高峰娟.灰色預測模型在軍機飛控系統故障預測中的應用[J].四川兵工學報,2014,35(6):44-46.

[10] Kayacan E,Ulutas B,Kaynak O.Grey system theory-based models in time series prediction [J].Expert Systems with Applications,2010,37(2):1784-1789.

[11] Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1/2):229-244.

[12] Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-838.

[13] Qiu G,Shentu N,Shi Z.Prediction method of cement strength based on GM-RBF neural network combination model [J].Science & Technology Review, 2014,32(3):56-61.

[14] Li S,Mei Q.Public-key coding system based on grey generation and braid group [J].Grey Systems:Theory and Application,2011,2(3):419-426.

(編輯：任亞超)

Design of flight controller based on grey-prediction sliding mode control

JIAO Xin, JIANG Ju, MENG Hong-peng

(College of Automation Engineering, NUAA, Nanjing 210016, China)

This paper proposed a novel scheme that applied grey theory in the field of flight control for the first time, considering the unavoidable uncertainties and external disturbances of near-space morphing aircraft flying in complex aerospace environment. After analyzing the uncertainties existing in the nonlinear model of near-space morphing aircraft, GM(0,N) was drawn upon to accurately forecast the parameter uncertainties and external disturbances. In terms of the values of prediction, the robust controller based on grey prediction was designed to compensate the influences caused by uncertainties and disturbances. Simulation results indicate that GM(0,N) is effective to predict the uncertainties and external disturbances which can be completely compensated by the proposed robust controller to gurantee the stability and robustness of the near-space morphing aircraft.

grey prediction; GM(0,N) model; near-space morphing aircraft; flight controller

2015-04-21;

2015-08-17;

時間:2015-09-25 16:10

江蘇省普通高校研究生科研創新基金資助(CXZZ13_0170)；校博士學位論文創新與創優基金資助(BCXJ13-06)；中央高?；緲I務費專項基金資助

焦鑫(1986-)，女，山西永濟人，博士研究生，研究方向為先進飛行控制技術； 江駒(1963-)，男，江蘇揚州人，教授，博士，研究方向為導航、制導與控制； 孟宏鵬(1989-)，男，河南鄭州人，碩士研究生，研究方向為系統工程。

V249.1

A

1002-0853(2015)06-0542-05