基于改進函數替換法的變形無人機LPV系統建模

吳成富, 邵朋院

(西北工業大學 無人機特種技術國家重點實驗室, 陜西 西安 710065)

基于改進函數替換法的變形無人機LPV系統建模

吳成富, 邵朋院

(西北工業大學 無人機特種技術國家重點實驗室, 陜西 西安 710065)

為了提高函數替換法的適用范圍,對現有的函數替換法進行了分析,提出了一種改進的函數替換法,并使用該方法建立了變形無人機的縱向LPV模型。首先,對現有的LPV系統建模方法進行了總結,通過在函數替換法基礎上引入部分線性化,使變參數的選取更為靈活,增強了函數替換法的實用性;然后,以變形無人機縱向系統為例,給出了基于所提出方法的縱向LPV系統模型;最后,對所建立模型的有效性進行了驗證。結果表明,所建立的模型與原始非線性模型近似程度很高,證明了該方法的有效性。

LPV系統; 系統建模; 變形無人機; 函數替換法

0 引言

在控制工程中,多數系統均為非線性、時變且不確定的,如本文研究的變形無人機(MUAV)。雖然在理論上非線性控制、魯棒控制和自適應控制等先進控制方法可以解決上述問題,但是在工程實際中這些方法常常難以應用。在工程實際中,應用最多的仍然是基于線性定常(LTI)系統模型的PID控制[1]。在處理非線性、時變特性和不確定性時,工程中常用的方法是增益調度PID方法[2]。這種增益調度方法雖然可以處理很多實際的非線性參變系統的控制問題,但其理論基礎仍然是基于LTI系統的線性控制理論，所以無法從理論上保證被控系統在整個運行包線范圍內的魯棒性和穩定性。

針對此問題,Rugh和Shamma[3]提出了線性變參數系統(Linear Parameter Varying, LPV),該系統具有LTI系統的形式,并引入了變參數。理論研究表明,非線性系統都可以轉化為LPV系統來研究其控制問題;由于形式相同,可以將對于LTI系統的研究結論拓展到LPV系統。因此,LPV系統的概念一經提出,便成為控制學界一個新的研究熱點。

模型建立是控制的基礎,系統建模也成為LPV系統控制研究的一個重要問題。與其他系統類似,LPV系統的建模方法也可以分為機理建模和系統辨識兩類。由于飛行力學的發展,對于飛機的氣動力學和運動學機理已經具有較為深入的認識,本文主要研究機理建模方法,即得到非線性模型之后,如何將其轉化成LPV系統模型。在總結現有LPV系統建模方法的基礎上,提出了一種改進的函數替換方法,并在MUAV的LPV建模中進行應用,證明了該方法的有效性。

1 一種改進的LPV系統建模方法

1.1 LPV系統的定義

LPV系統是指具有線性系統的形式,而系統中某些參數隨著外部參數的變化而變化的系統。用狀態空間形式表達如下:

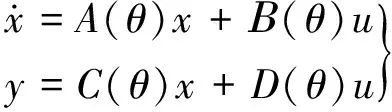
(1)

式中:x,u,y分別為系統狀態、控制輸入和量測輸出;θ為變參數向量,即θ=[θ1,θ2,…,θn]T。對于LPV系統,要求所有變參數是可測的;同時,對于實際系統,假設變參數及其變化率有界。

1.2 改進的函數替換法

本文中的LPV系統建模特指將非線性模型轉化為LPV系統模型。即將如下系統轉化為系統式(1)的形式:

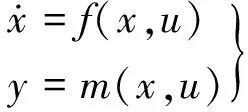
(2)

在現有文獻中,LPV系統的建模方法一般有如下幾種:雅克比線性化方法[4]、狀態變換法[5]、基于速度的線性化方法[6]和函數替換法[5]。由于采用函數替換法進行LPV建模時必須將所有與非線性有關的狀態納入變參數,若非線性相關的狀態不可測量,則函數替換法無法應用。改進方法的核心思想是將與非線性有關的狀態中不能或不需要納入的變參數進行線性化。

下面進行詳細說明。為簡明起見,只對狀態方程進行函數替換,輸出方程類似,在此不再贅述。

對系統式(2),設x=[x1,x2,x3]T,其中x1和x2為與非線性有關的狀態,x3為與非線性無關的狀態。

則系統式(2)中的狀態方程可以寫成:

(3)

若使用原始的函數替換法,則需要將x1和x2均納入變參數,若x1不可測或者得到的變參數過多,則需要將x1從變參數向量中剔除,本小節通過對x1進行線性化,從而將x1從變參數向量中剔除。

選取參考點x0=[x10,x20,x30]T,定義新狀態變量dx1=x1-x10,并在該參考點處對x1進行線性化。定義輔助函數:

(4)

則有:

(5)

上式中與x2無關的非線性項只有

(6)

再定義dx3=x3-x30,將x3線性化并省略一階小量的乘積項,則有:

Δgx3=g(x10,x2)x30+g(x10,x2)dx3+

(7)

若對x1線性化之后無與x3有關的乘積項,則對x3線性化的步驟可以省略。非線性項剩下與x2有關的項,對這些項進行函數替換,即可得到變參數只包含x2的LPV系統。

2 在變形無人機建模中的應用

本文研究對象為Z型折疊翼變形無人機,其機翼分內外兩段,內段機翼可以繞旋轉軸轉動,在內段機翼轉動時,外段機翼始終保持水平,如圖1所示。

圖1 變形無人機展開和折疊構型Fig.1 Expanding and folding configurations of MUAV

下面使用改進的函數替換法來建立變形無人機的LPV模型。為簡明起見,只建立其縱向系統模型。飛機的六自由度方程見文獻[7],結合方向余弦矩陣,可以分離出縱向運動方程為:

(8)

式中:u,w分別為機體軸Ox和Oz軸方向的速度分量;q為機身俯仰角速率;θ為俯仰角;M為俯仰力矩;Iyy為繞機體軸Oy軸的轉動慣量;Fx和Fz分別為合外力沿機體Ox和Oz軸的分量,如下式所示:

(9)

式中:T,L,D分別為飛機的發動機推力、升力和阻力,L和D的組成和計算參見文獻[7]。假設發動機推力線過重心,且發動機安裝角為0°。

設飛機的氣動系數和導數可以表示為C*=f*(v1,v2,…),其中“*”表示氣動力或力矩;v1,v2,…表示查表的索引項。例如升力對升降舵的導數表示為:

CLδe=fLδe(α,θr,δe)

通過觀察氣動系數可以發現,飛機的舵偏輸入以及油門輸入與輸出的力和力矩近似呈線性關系,所以,可以將輸入進行線性化。例如,對于升降舵,可以近似認為下式成立:

f*(α,θr,δe)=f*(α,θr)δe

其他控制的處理方法類似,處理之后所有的氣動系數和氣動導數均可以表示成α和θr的函數,聯立以上各式,可以得到:

(10)

式中:Q為動壓;Sw為機翼參考面積。為簡明起見,在表達式中將氣動系數中的變參數項α和θr省略。

非線性項中包含了速度分量u和w,迎角α,折疊角θr,俯仰角θ和馬赫數Ma。可以看出,非線性項與θ的非線性關系最為簡單,僅有sinθ和cosθ兩項,所以用對θ的線性化來說明如何通過部分線性化來減少必須包含的變參數個數。

選取參考點θ0,對三角函數進行線性化,如下式所示:

(11)

將式(11)代入式(10),并定義dθ=θ-θ0,可得:

(12)

選取狀態變量為x=[u,w,q,dθ]T,輸入為u=[δe,δT]T,則可以將式(12)表示成如下的狀態空間形式:

(13)

其中,系統A和B矩陣中各項分別為:

(14)

非線性項h中的各項為:

hu=m-1QSw(fCLcosα-fCDsinα)-gsinθ0

(15)

hw=gcosθ0-m-1QSw(fCLsinα+fCDcosα)

(16)

(17)

以上討論中,變參數中的機體軸速度分量u,w是不能直接測量的,在無風假設下,這兩個量與飛機的空速V和迎角α是等價的,有如下關系成立:

(18)

在飛機飛行高度變化不大的前提下,Ma和V也是對應的,所以,式(12)中的LPV系統的變參數向量可以選取為θ=[V,α,θr]T。對于查表的非線性關系,例如氣動系數,可以采用多項式擬合獲得其解析形式,多項式的形式可以通過觀察氣動數據曲線獲得。

以Cmq為例,通過觀察氣動系數曲線,可以看出其與α近似呈三次多項式關系,與θr近似呈四次多項式關系,故采用如下多項式形式:

fCmq(α,θr)=a0+a1α+a2α2+a3α3+

(19)

使用吹風數據進行擬合,得到各個系數值:a0=-8.605 9,a1=-0.212 6,a2=-15.839 7,a3=52.424 9,b1=2.890 7,b2=-3.833 4,b3=2.416 7,b4=-0.525 3。將結果代入式(19),在吹風數據點處由下式求出擬合值和實際吹風值的相對誤差:

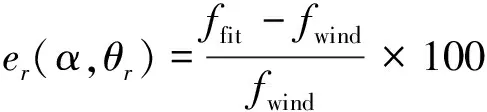
(20)

式中:ffit為擬合數據;fwind為吹風數據。

計算結果如圖2所示。由圖可知,擬合結果的最大誤差不超過1.5%,擬合誤差較小,在工程容許的誤差之內。

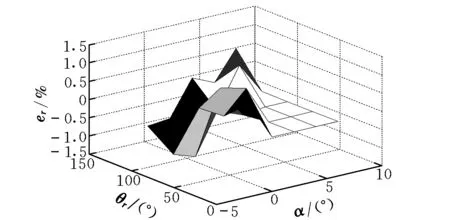
圖2 擬合數據和吹風數據相對誤差曲線Fig.2 Relative error between fitted data and wind-tunnel data

將擬合結果代入式(12),即可得到解析形式的LPV模型。

3 仿真結果及分析

將建立的LPV模型與原始非線性模型響應進行對比,給定初始狀態為空速25 m/s,折疊角θr為0°的配平狀態,在仿真進行2 s時,機翼以20 (°)/s的速率進行折疊,到8 s時折疊角達到120°,之后保持2 s,得到各個量的響應如圖3～圖5所示。

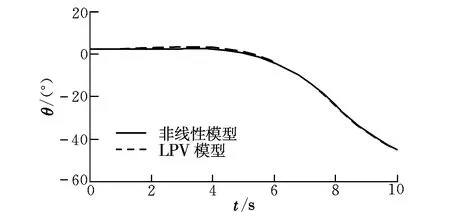
圖3 俯仰角響應曲線Fig.3 Responses of angle of pitch

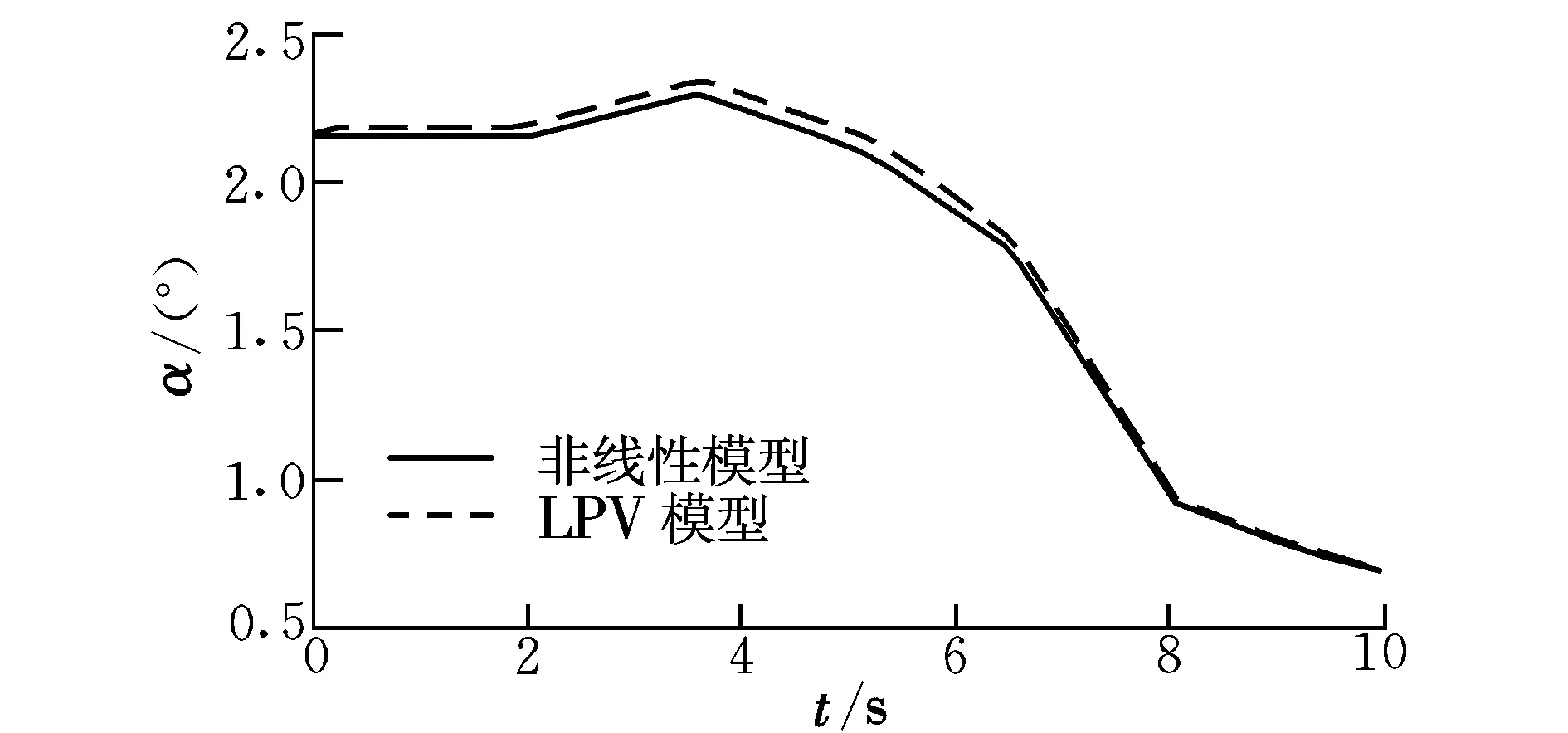
圖4 迎角響應曲線Fig.4 Responses of AOA

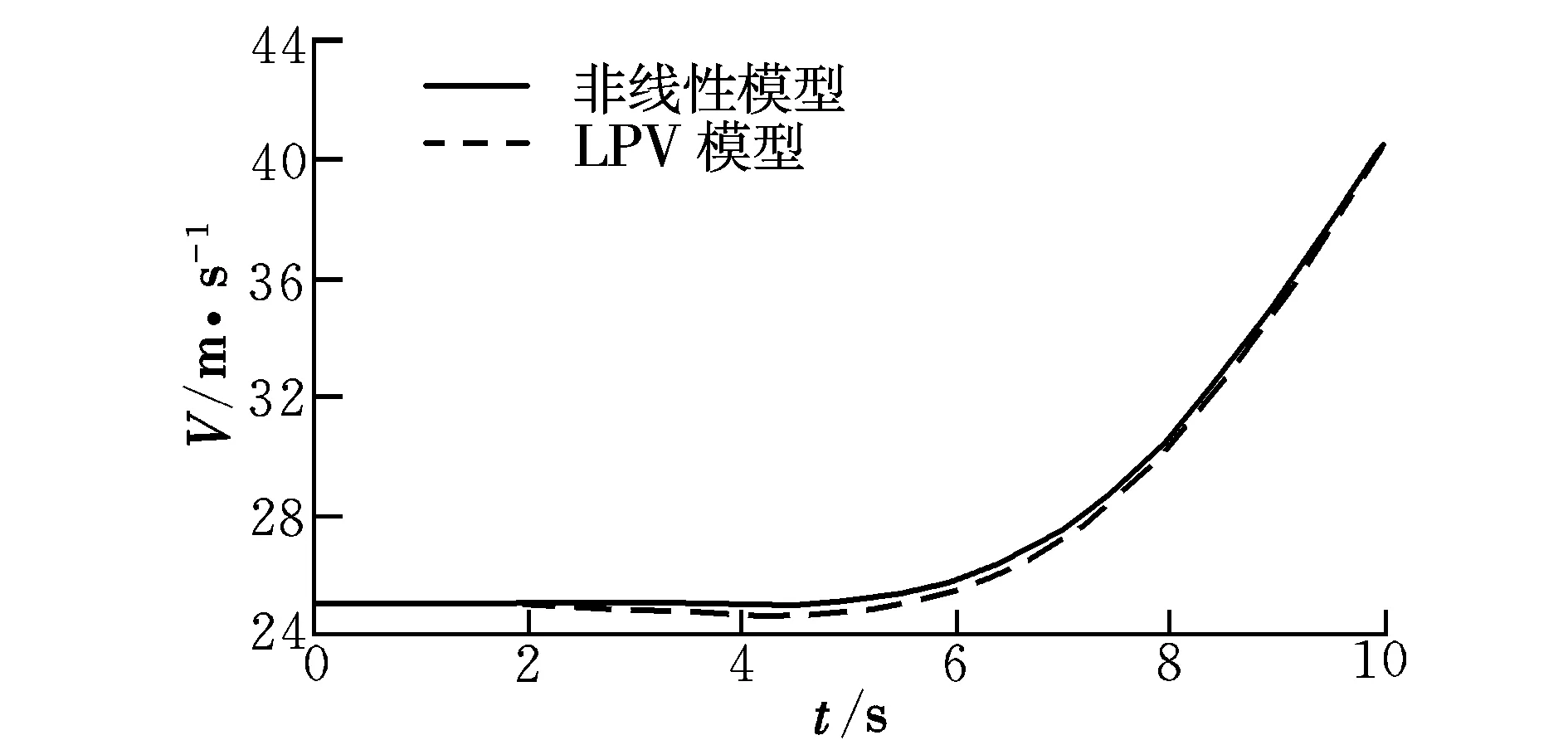
圖5 空速響應曲線Fig.5 Responses of airspeed

由圖3～圖5可以看出,所建立的LPV模型與原始非線性模型響應十分接近,迎角和俯仰角的響應誤差均小于0.5°,空速響應誤差小于1 m/s,所以文中提出的建模方法是可行的。如果減小線性化區間間隔,則建模誤差可以進一步減小。

4 結束語

針對函數替換法不能自由選取變參數的缺點,通過引入部分線性化對其進行改進,使用改進方法建立了變形無人機的縱向LPV系統模型。與原有的函數替換法相比,該方法的優點在于可以自由選取變參數,從而增強了函數替換法的應用范圍。

由于引入了線性化,該方法與原有的函數替換法相比存在一定的建模誤差,雖然建模誤差可以通過增加線性化的網格密度來減小,但是網格密度的選取尚無理論方法可用,只能依據實際的對象,按照經驗選取,這是該方法需要進一步研究的問題。

[1] Ang K H,Chong G,Li Y.PID control system analysis,design,and technology[J].Control Systems Technology,IEEE Transactions on,2005,13(4):559-576.

[2] Shamma J S,Athans M.Analysis of gain scheduled control for nonlinear plants[J].Automatic Control,IEEE Transactions on,1990,35(8):898-907.

[3] Rugh W J,Shamma J S.Research on gain scheduling[J].Automatica,2000,36(10):1401-1425.

[4] Shin J Y.Quasi-linear parameter varying representation of general aircraft dynamics over non-trim region[R].NASA/CR-2007-213926,2007.

[5] 李文強.LPV系統魯棒變增益控制研究及其應用[D].長沙:國防科學技術大學,2009.

[6] 王青,王通,后德龍,等.基于速度線性化的變體飛行器魯棒變增益控制[J].系統工程與電子技術,2014,36(6):1130-1136.

[7] 吳森堂,費玉華.飛行控制系統[M].北京:北京航空航天大學出版社,2005:58-59.

(編輯：任亞超)

LPV modeling of morphing UAV based on improved function-substitution method

WU Cheng-fu, SHAO Peng-yuan

(National Key Laboratory of Special Technology on UAV, NWPU, Xi’an 710065, China)

To enhance the applicability of function-substitution method, an improved function-substitution based modeling method for LPV systems is proposed and applied on modeling of the longitudinal system of morphing UAV. Partial linearization is introduced to function-substitution method, thus the varying parameters can be chosen more flexibly and the number of varying parameters can be reduced. After that, the LPV model for longitudinal system of morphing UAV is derived using the proposed method and the simulation result shows that the responses of LPV model is highly consistent with the nonlinear model.

LPV system; system modeling; morphing UAV; function-substitution method

2015-01-15;

2015-05-18;

時間:2015-09-25 16:10

吳成富(1962-)，男，浙江金華人，教授，博士生導師，主要研究方向為無人機導航、制導與控制； 邵朋院(1986-)，男，陜西咸陽人，博士研究生，主要研究方向為無人機導航、制導與控制。

V279

A

1002-0853(2015)06-0565-04