分圖分類分析
——一道中考操作題的解法探究及分析思考
☉江蘇省宿遷市實驗學校 李軍
分圖分類分析
——一道中考操作題的解法探究及分析思考
☉江蘇省宿遷市實驗學校 李軍
一、原題呈現
題目(2015年南京市第25題)如圖1,在邊長為4的正方形ABCD中,請畫出以A為一個頂點,另外兩個頂點在正方形ABCD的邊上,且含邊長為3的所有大小不同的等腰三角形.(要求:只要畫出示意圖,并在所畫等腰三角形長為3的邊上標注數字3)

圖1
二、解法探索
1.“圓規”探究法
(1)以3為等腰三角形的“腰”.
①兩腰都在正方形邊上,如圖2;②一腰在正方形邊上,如圖3、圖4.
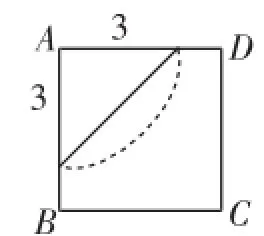
圖2

圖3

圖4

以A為圓心,3的長為半徑畫弧,與邊AB、AD相交即可.先畫OA=3,再以O為圓心,3的長為半徑畫弧,與邊CD相交即可.同圖3,大小也相同,兩圖畫出一個即可.
(2)以3為等腰三角形的“底”.
①“底”在正方形邊上,如圖5、圖6;
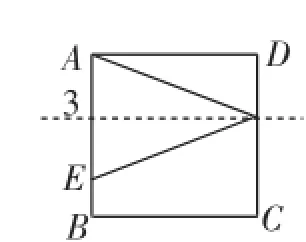
圖5

?
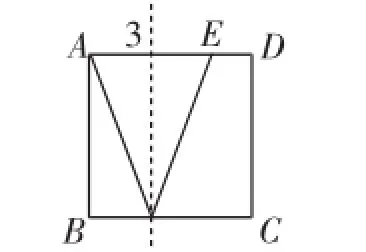
圖6
②“底”不在正方形邊上(先是兩腰在正方形邊上,然后是兩腰不在正方形邊上),如圖7、圖8.
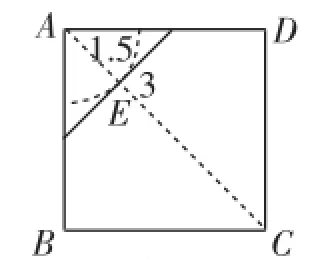
圖7

圖8

同圖7,也可作出圖7中的已作線段關于對角線BD的對稱線段即可.以A為圓心,1.5的長為半徑畫弧,與對角線AC相交于點E,過E作AC垂線與正方形兩邊相交即可.
2.“網格”探究法
根據題目條件,將邊長為4的正方形放置到對應邊長為1的正方形網格中加以探究,有了網格便可以通過觀察,借助刻度尺或圓規等工具將問題解決(如圖9~15便一目了然,畫法略).
(1)以點A為兩腰交點思考(先是兩腰在正方形邊上,然后是兩腰不在正方形邊上,如圖9~11).
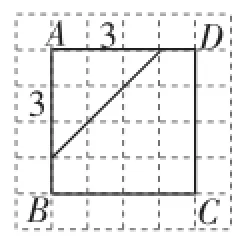
圖9
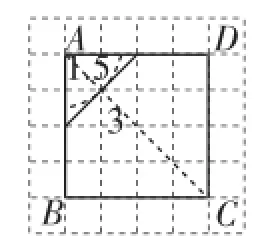
圖10
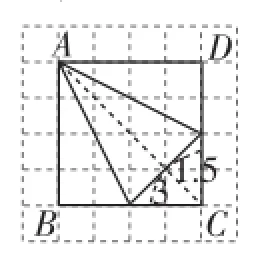
圖11
(2)以點A為底與腰交點思考(先是底在正方形邊上,再是腰在正方形邊上,如圖12~15).
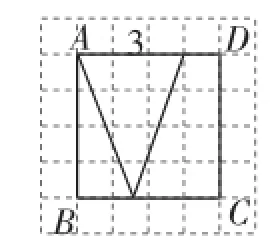
圖12
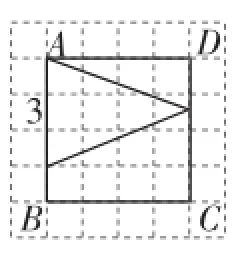
圖13
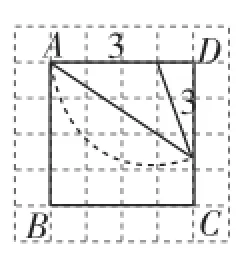
圖14
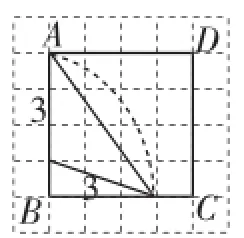
圖15
3.“折紙”探究法
因給定的圖形及組合后的部分圖形為軸對稱圖形,故筆者想到用“折紙法”進行探究,并進行了“折紙”試驗,以上圖形均可由“折疊”得出.
將給定的正方形做成正方形紙片,沿橫向與縱向各折疊兩次,便在正方形各邊上得到“數值點(線)”(如圖16),然后再分別以3為等腰三角形的“底”及以3為等腰三角形的“腰”兩類分別折疊便可得出圖形,如圖17~23.
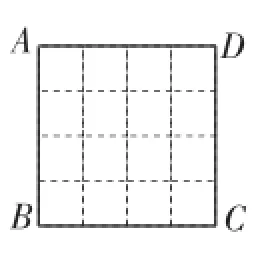
圖16
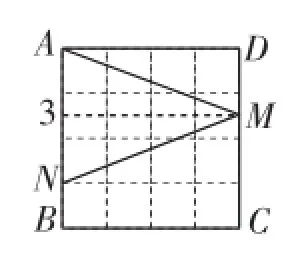
圖17

圖18
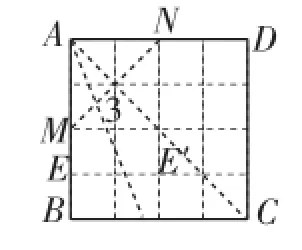
圖19
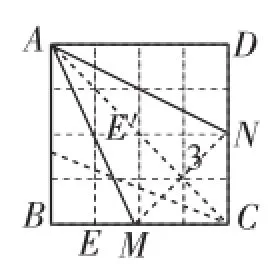
圖20

圖21

先折出對角線AC,再沿∠BAC的平分線折疊,在AC上使AE′= 3,再沿AE′的中垂線折疊即可.
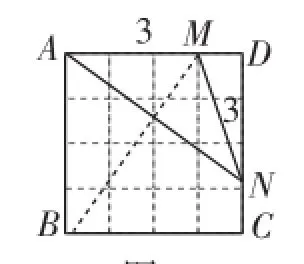
圖22
圖23
三、特色分析
1.設計簡明 立意操作
從選材看,選取學生特別熟悉的正方形和等腰三角形作為背景圖,以生為本,簡單美觀;從語言表述看,簡潔明確,要求具體,操作指向明了;從構思看,在操作中提煉“模型”,重視基礎(基礎圖形、基礎知識、基本操作),呈現層次性(學生會由簡單入手,分層思考)和多樣性(會呈現出不同的豐富多彩的情況).
2.易于動手 引領探究
此題操作起點低、入口寬,不同層次的學生均可以動手嘗試,會盡自己所能畫出能想到的圖形,當然也能得到相應的分數.由于學生易于動手,所以問題情境能激發學生的探究欲望,不斷激勵學生去向更多、更深的方向思索與邁進,簡單的問題鋪設著“過程性”道路,突出延展了問題思考過程與操作過程.
3.關注經驗 突出分類
“基本活動經驗”是《義務教育教學課程標準(2011年版)》新增的課程目標,將原有的“雙基”教學發展為“四基”教學.本題的考查,就是立足于學生的基本經驗,有的通過觀察比劃即可畫出圖形;有的需借助圓規操作,圖形就會顯現出來;有的需要分析思考,多次嘗試才能得出答案.
《義務教育數學課程標準(2011年版)》指出:“分類是一種重要的數學思想.學習數學的過程中經常會遇到分類問題,如數的分類、圖形的分類、代數式的分類、函數的分類等.……分類的過程就是對事物共性抽象的過程.……學會分類,可以有助于學習新的數學知識,有助于分析和解決新的數學問題.”
本例屬于典型的圖形分類問題,突出考查學生在操作的同時要學會分類,同時指引學生可以從“形”和“數”兩個角度加以分類(上述方法從不同側面進行了探討),即以固定不動的點A為分類點,分點A為兩腰的交點及腰與底邊的交點兩大類,或以數量“3”為出發點,分以3為等腰三角形的“腰”與以3為等腰三角形的“底”兩大類.這樣就會做到“不重不漏”,完整解答.
四、命題建議
若能在原有問題基礎上增加“求出相應的等腰三角形面積”,則問題將變得更豐富、更有內涵,更能引發學生去思考、去計算,進而去聯系更多的知識,構建“點線式”知識網絡,或許對學生綜合能力的培養及思維的發展會大有裨益.
五、教學思考
1.多維探究,解題策略優化互補
日常教學中,應在學生已有的知識儲備上,適時引導學生從不同角度思考問題,發散學生的思維,以提升學生解決問題的實際能力和思維水平,如果學生平時解題僅僅停留在為解題而解題、就題論題的層面上,靠題海戰術和老師的灌輸獲得解題技巧,而很少經歷探索、思考的過程,就不能養成思考的習慣,只能模仿和套用已有的知識儲備,學生則不能形成真正的數學能力.
對于本題提供的三種操作思路,學生并不陌生,它是操作類題中經常涉及的(使用作圖工具、正方形網格、折紙操作),不同的操作策略有不同的特點,教學時引導學生多方位思考,既培養學生解題的靈活性,也訓練了學生的發散思維,還可以啟發學生比較優劣,從而優選方案,更優更快地分析問題和解決問題.
2.重視操作,培養動手畫圖能力
操作類試題一般在中考中較難考查,此題為此搭建了很好的平臺,對教學起到了較好的引領作用.平時教學中,教師不能一味地讓學生埋頭做計算題和推理題,更要在操作中培養學生的動手能力和創新精神,讓學生在“做數學”中激發興趣,發現結論,總結規律,掌握其操作方法,學會思考.本題可借助圓規,找到關鍵點就可把所有情況一一畫出來,讓學生知其然,更要知其所以然.如若本題僅僅是結果的展示,則失去了“數學本真”,也不符合學段特征(初中學段——尺規作圖、合情推理、邏輯推理等).
3.規范指導,反思過程
畫圖的過程是學生動手操作的過程,也是幾何直觀的具體體現,通過捕獲作圖過程中的信息尋找解決問題的切入口,在教學中重視培養學生的畫圖習慣,教師首先要做出示范.畫圖類問題在操作時,若教師平時重視不夠或操作示范性不夠嚴謹,自然就會導致學生畫圖不認真、不仔細,任意涂改,造成所畫圖形雜亂,以致引發思考淺浮,思維混亂.本題學生或許能畫出部分圖形,但如不規范操作,耐心思考,想完整全面答出此題也是望塵莫及的.這就要求在日常的教學中,一方面教師要做好表率作用,另一方面也要求學生認真對待,規范操作,條理思考,將圖形畫得準確、美觀、完全.
美國教育心理家布魯納指出:掌握基本的數學思想方法,能使數學更易于理解和更利于記憶,領會基本數學思想和方法是通向遷移大道的“光明之路”.在人的一生中,最有用的不僅是數學知識,更重要的是數學的思想方法和數學的意識,因此數學思想方法是數學的靈魂和精髓.操作類問題其實也蘊含著一定的知識和思想方法,需要師生共同總結思考,雖然本題考查的知識點不是很豐富,其關鍵是要能學以致用,其中有分類討論、類比轉化、特殊與一般、圖形變換等重要數學思想,值得我們深思.
1.湯妙娟.對一道中考題的賞析、探究及反思[J].中學數學(下),2015(6).
2.由學芹.再說“數學好玩”[J].中學數學(下),2012(9).
3.張俊.一道試題的多解思考及其教學展望[J].中學數學教學參考(中),2013(8).
4.中華人民共和國教育部制定.義務教育數學課程標準(2011年版)[M].北京:北京師范大學出版社,2012.H

