緊扣信源特點析題抓住關鍵信息建模*
——談中考應用型問題的講評策略

緊扣信源特點析題抓住關鍵信息建模*
——談中考應用型問題的講評策略

☉江蘇省如皋市下原初中吳文俊

在中考中，應用型問題是一種常見題型，以代數式、方程（組）、不等式和函數等為主要考查對象.這類考題一般取材于學生熟悉的生活情境，以文本、表格、圖像等形式呈現試題信息.這類考題由于信息量大，信息傳遞形式復雜，成為了學生的應試難點.為了幫助學生形成突破這一難點的策略，我們可以抓住“信源”（信息的載體）特點詳細剖析題目，抓住捕獲到的關鍵信息建構解題模型化解問題.

一、拆解函數圖像，挖掘適用模型

以圖像作為信源的應用型問題在中考中是最常見的.一兩幅圖像，配上少量的文本信息，讓試題看起來簡潔明了，但實際求解卻面臨眾多問題.能不能讀懂圖像，能不能將圖像和文本對應起來，能不能抓住圖像和文本的關鍵信息建構適用的解題模型，這些將都影響著問題的解決.

例1甲、乙兩車從A地駛向B地，并以各自的速度勻速行駛，甲車比乙車早行駛2h，并且甲車途中休息了0.5h，如圖1，是甲乙兩車行駛的距離y（km）與時間x（h）的函數圖像.

（1）求出甲車行駛路程y（km）與時間x（h）的函數解析式，并寫出相應的x的取值范圍；

（2）當乙車行駛多長時間時，兩車恰好相距50km.

1.例題分析

這道試題的信源是一幅圖像和幾段文本，其中，文本信息量較小，題干部分只有75個字.顯然，本題的解答就應從圖像入手了.從圖像看，第（1）題所求的y與x的函數解析式對應著圖中的折線OABD，這是一個分段函數，OA對應著范圍0≤x≤1，AB對應著范圍1＜x≤1.5，BD對應著范圍1.5＜x≤7，只要將這些對應段內的函數關系式求出即可解答第（1）題.第（2）題，“兩車恰好相距50km”包含兩種可能：①甲車行駛路程y（km）（下稱y甲）比乙車行駛路程y（km）（下稱y乙）多50km；②y甲比y乙少50km.體現在圖像上，就是“x取同一值時，線段BD位于線段EF的上方或下方50km處.這樣一來，在求出BD的解析式后，就可以直接借助兩條線段的位置關系建立不同的方程求解.

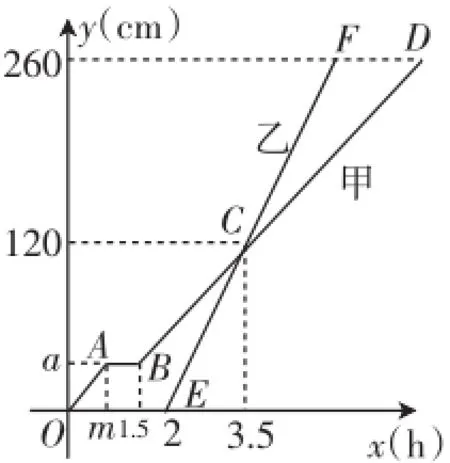
圖1

2.教學簡錄

（1）拆圖.

問題：①圖像中共有幾條線？②是什么線？③這些線一般與什么函數有關？

學生圍繞問題組展開討論，將圖中的折線OABD與分段函數、線段EF與一次函數關聯在一起.

（2）析點.

學生活動：找出圖像中的幾種特殊點：起點、終點（說明：教學時，我們默認線左側的端點是起點，右側的端點為終點，下同）、交點和拐點，并說說它們的含義.

學生將圖像和文本對應在一起，將圖1中的O，A，B，C，D，E，F這七個點的含義在小組中進行了交流，并將能寫出的坐標標注在圖像上.

（3）建模.

學生活動：先分別求出圖1中的線段OA，BC，EF的解析式，再思考例1中的兩個問題該如何解答.

學生用待定系數法分別求出了解析式，并在小組中交流了例1的解法.教師對學生給出的解法進行了點評，并將第（2）題的兩種情況進行了投影.

3.過程簡析

函數圖像信息題，因為圖像的存在而得名，圖像也就成為了學生審題的難點.拆圖，讓復雜的圖形簡單化，學生會努力將圖像與自己學過的函數關聯起來，與問題解決關聯不大的信息會自然淡出；析點，讓關鍵點“浮出水面”，理清這些點的坐標的實際含義與圖像含義，將會為模型的建構掃清障礙；建模，基于線與圖像關系的分析和點的坐標的分析，在文圖呼應中，函數模型自然生成，由此生成的方程、不等式等模型就成為了學生化解問題的工具.拆圖—析點—建模，這不僅是教師的教學歷程，更應成為學生分析函數圖像信息題的歷程，是學生獲得正確解題思路，形成規范解題過程的必經步驟，我們應在教學中，將這一程序化分析套路滲透在教學之中，使其內化為思維習慣，外顯為解題行為.

二、剖析關鍵詞句，準確關聯模型

在中考中，還存在著一些只有文本信息的應用型問題.這類考題，只通過文本傳遞信息，題目中不存在表格或圖像等其他信息.豐富的文本信息中，既包含著緊貼學生實際生活的問題情境，還包含著能夠解決問題的數學模型.為了找尋這些“或隱或現”的數學模型，我們應加強審題指導，讓學生將關鍵詞句與常見數學模型關聯起來，形成問題解決的常用套路.

例2某校計劃購買甲、乙兩種樹苗共1000株用以綠化校園，甲種樹苗每株25元，乙種樹苗每株30元，通過調查了解，甲、乙兩種樹苗成活率分別是90%和95%.

（1）若購買這種樹苗共用去28000元，則甲、乙兩種樹苗各購買多少株？

（2）要使這批樹苗的總成活率不低于92%，則甲種樹苗最多購買多少株？

（3）在（2）的條件下，應如何選購樹苗，使購買樹苗的費用最低？并求出最低費用.

1.例題分析

這道試題的題干和問題都是以文字信息給出的，作為信息源頭的文本，承載著大量信息.因此，解答本題應從文本入手，剖析題中的關鍵詞，找尋出問題解決的數學模型.問題（1），兩個“共”字，給出兩個等量關系“甲種樹苗的棵樹+乙種樹苗的棵樹=1000”和“甲種樹苗的費用+乙種樹苗的費用=28000”，這是建立方程組的依據；問題（2），抓住題中的關鍵詞“不低于”可以建立不等式模型求解；問題（3），“費用最低”指向了函數，利用“買樹苗的費用”與樹苗棵樹之間的關系建立函數模型，再結合問題（2）中的取值范圍確定一次函數的最大值，問題就可以得到化解.

2.教學簡錄

學生活動：認真閱讀例2，將你認為重要的詞句用筆畫下來，并想一想這些語句與哪些數學模型有關.

學生讀題，教師巡視，并對學生標注進行指點.3分鐘后，教師組織學生開始全班交流.

教師：你畫出來哪些關鍵詞句呢？

學生1：我畫的是“共1000株”，“共用去28000元”，“總成活率不低于92%”和“費用最低”這四處.

教師：為什么畫這些呢？

學生2：這些關鍵詞與數學模型有關.

教師：是嗎？

學生3：“共1000株”，“共用去28000元”是明顯的等量關系，可以建構出方程模型；“總成活率不低于92%”中的“不低于”很明顯是個不等式模型；第（3）題中，根據題意可得，“費用最低”一定與函數有關.

教師：具體說說與哪些函數有關？

學生4：初中階段學過的三種函數都有關系，其中用的比較多的是帶取值范圍的一次函數和二次函數.

教師：看來最值問題與函數有關在你們的腦海中已經扎根了.接下來，就請大家根據你們的標記和發現的解題模型解答這道例題.

3.過程簡析

文本類“信源”，一般會將題中數量關系與變化規律蘊藏在關鍵詞句中.教者抓住這道例題中的信源特點，讓學生通過“讀題標注”的形式，將關鍵信息“定格”，為建構出有效解題模型夯實了基礎.例題中的兩個“共”字包含著“和”的味道，是列方程的依據；“不低于”可以轉化為數學符號“≥”，這是明顯的不等式標記；“最低”說明要求“極值”，這與函數是一定有關聯的.學生的標注與解讀，將關鍵詞句與數學模型緊密聯系在一起，問題解決的思路變得十分清晰.接下來，在學生的自主解答和全班交流中，審題成果轉化為解題過程，強化了學生對“關鍵詞句的解題作用”的體驗與感悟，這對他們的分析問題和解決問題能力的提升是大有益處的.

三、解讀表格信息，建構適用模型

初中階段，表格也常作為“信源”存在于應用型問題中.一般地，表格由一行或多行單元格組成，表格的第一行或第一列為表頭，它指明了表格的內容和意義.由此可見，解讀表格信息應從表頭入手，明晰表頭的含義，在弄清表頭所對應的列或行的含義的基礎上，理清表格中每一個單元格的實際意義，從而與方程、不等式及函數等數學模型關聯起來，找到問題解決的便捷通道.

例3某市政府為了增強城鎮居民抵御大病風險的能力，積極完善城鎮居民醫療保險制度，納入醫療保險的居民的大病住院醫療費用的報銷比例標準如下表：

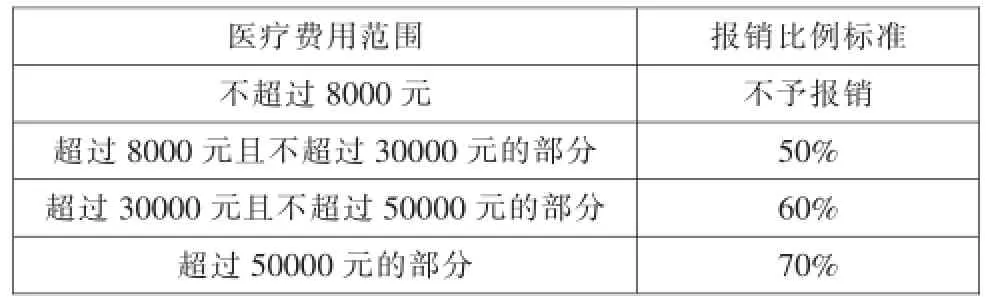
醫療費用范圍報銷比例標準不超過8000元不予報銷超過8000元且不超過30000元的部分50%超過30000元且不超過50000元的部分60%超過50000元的部分70%

設享受醫保的某居民一年的大病住院醫療費用為x元，按上述標準報銷的金額為y元.

（1）直接寫出x≤50000時，y關于x的函數關系式，并注明自變量x的取值范圍；

（2）若某居民大病住院醫療費用按標準報銷了20000元，問他住院醫療費用是多少元？

1.例題分析

很明顯，本題重點考查了一次函數的應用，試題選擇了表格作為信息的主要呈現方式，將“醫療費用范圍”及與之相對的“報銷比例標準”對應呈現在表格之中.在這張表格中，表頭安排在第一行，詳細闡述了表格的兩列的含義，第一列為“醫療費用范圍”，第二列為“報銷比例標準”.解答此題，解讀表格成為了關鍵.首先，要弄清楚x、y的意義和表格中單元格的意義，再結合表格中的信息對報銷金額y（元）進行分段，根據表格信息，問題（1）中的y被分為3段：“0＜x≤8000”，“8000＜x≤30000”，“30000＜x≤50000”，抓住表格中的分段信息，求出函數關系式，問題（1）得解.問題（2），先要確定20000元的報銷額度落在函數的哪一段中，從而利用對應段的函數關系式建構方程求解.

2.教學簡錄

學生活動：學生讀題，并在小組中交流各自獲得的信息.3分鐘后，小組交流結束.

教師：說說你獲得的信息吧！

學生1：“報銷比例標準”共分為四段，8000元，30000元，50000元是三條分界線，表格中給出了詳細的報銷比例.

教師：真不錯！你是怎么找到這些分界線的？

學生2：表格共兩列，第一列第一行是“醫療費用范圍”，第二列第一行是“報銷比例標準”.

教師：這兩個單元格告訴我們什么？

學生3：“醫療費用范圍”這一列，將醫療費用的范圍進行了分段，“報銷比例標準”這一列給出了與第一列的范圍對應的報銷比例.

教師：說得很好！看來我們解讀表格應從表頭入手，不僅要弄懂每一個單元格的意義，還要將表格中的單元格對應起來，剖析其中的數量關系和變化規律.接下來，就請大家用你們獲得的信息解決這道例題.

3.過程簡析

應用型問題的信息傳遞方式很多，表格是較為常見一種方式.為了培養學生解讀表格，從表格中捕獲有用解題信息的能力，教者在學生自主審題后，讓他們將自己獲得信息在小組和全班進行了交流，通過不同層面的交流，學生將自己獲取信息的過程重新梳理一遍，將解讀表格信息的方法內化為個體經驗.在歷經多次強化訓練后，這種個體經驗將會逐步轉化為個體的解題行為，使學生在解決表格信息型問題時能“從表格的表頭入手，緊扣單元格意義”逐級分析，找出其中的數量關系和變化規律，從而建構出解題適用的數學模型.

應用型問題，是中考的熱點問題，其綜合性、時代性給試題的信息解讀增加了很大的難度.為了幫助學生形成應用型問題的個體化分析方法，我們應將不同信源的分析方法在教學中呈現給學生，讓他們在反復解答、交流中，將這些方法不斷內化，漸進中成為個體的分析和解題行為.要指導學生解讀不同信源的方法，圖像信源要立足文圖呼應，在拆解圖像中捕獲關鍵點；文本信源應從關鍵詞句入手，將文本與模型關聯起來；表格信源應從表頭分析出發，從單元格意義入手挖掘解題模型.總之，化解圖像信息題，應“緊扣信源特點析題，抓住關鍵信息建模”.H

*本文為江蘇省如皋市教育科學“十二五”規劃立項課題“提高初三綜合題評講效率的研究”的研究成果．本文作者系該課題主持人．