基于激光散斑角度相關法表面粗糙度測量
陳 晨,郭曉明,馬 軍,王文生*
(1.長春理工大學光電工程學院,長春130022;2.中國科學院長春光學精密機械與物理研究所,長春130033)
引 言
表面粗糙度是衡量精密零件加工質量的一個重要指標。隨著機械加工等工程領域的發展,對表面粗糙度測量的要求也越來越高。在表面粗糙度的測量中,光學方法具有非接觸、不損傷表面、精度高和響應快等優點,其測量原理種類繁多,主要的測量方法有:散射法、干涉法、光學觸針法、衍射法和散斑法等[1-2]。
散斑是相干光學中的一個現象,它是由于在粗糙表面(透射或反射)散射的光波疊加產生的,因此散斑圖像中攜帶了被照射表面的粗糙度信息,目前利用散斑方法測量物體表面粗糙度是實現非接觸、快速測量的一種有效方法,它克服了接觸式測量劃傷被測表面和效率低等缺點。測量表面粗糙度的散斑方法又分為散斑對比度法和散斑相關法。散斑對比度測量方法又分單色與多色、像面散斑與衍射面散斑對比度法,測量范圍較小,一般用于粗糙度小于0.25μm范圍內表面粗糙度測量,比較適用于光滑表面的粗糙度測量。散斑相關法測量范圍大,可以從0.6μm~13μm,甚至更大一些,因此該方法適合比較粗糙表面的測量。散斑相關法又分為角度散斑相關法[3]、雙波長散斑相關方法[4]、基于多色散斑延長效應的測量方法[5-6]等。
作者基于遠場角度散斑強度相關系數與表面粗糙度相關理論,設計了測量表面粗糙度的實驗光路,提出了基于MATLAB編程的自動尋找相關度峰值的數據處理方法,實現了表面粗糙度的準確快速測量。對平銑模塊的表面粗糙度進行了大量測量實驗,基于MATLAB軟件編寫程序,自動尋找相關度峰值,提高了相關度獲取速度,簡化實驗光路,增加了自動化程度,并最終驗證了利用激光散斑對表面粗糙度進行精確測量的可行性。
1 遠場角度散斑強度相關理論
1.1 角度散斑相關度與表面粗糙度的理論
散斑相關是指一個表面在兩種不同條件下產生的散斑圖樣間的相關度。通過改變入射角度或者被測表面旋轉微小角度,記錄改變前后兩幅散斑圖樣,這種方法稱為角度散斑相關。
如圖1所示,當束腰半徑為L、波長為λ的高斯激光束分別以角度α和角度α+δα先后入射到粗糙表面的同一區域時,入射光經表面散射后,在透鏡(焦距為f)的后焦面上形成兩個遠場散斑場。其強度分布分別為 I1(ξ,η)和 I2(ξ,η)。假設散斑場是由粗糙度參量比照明光束波長大得多的粗糙表面產生,同時粗糙面上有足夠多的相互獨立的散射元對復場振幅有貢獻,那么復場振幅將遵從經典圓型復高斯統計。根據基爾霍夫電磁波散射理論,可以得到任意兩點ξ1和ξ2所對應的散斑強度I1和I2的相關度γ為[7-12]:

式中,σ為粗糙表面的輪廓均方根偏差;k=2π/λ;f為透鏡焦距。
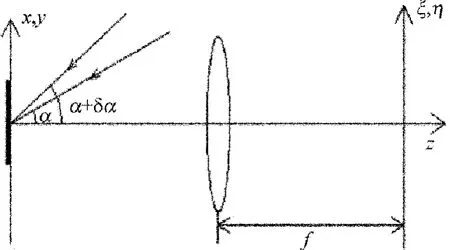
Fig.1 Schematic diagram of far-field angular-speckle correlation
相關度γ又可以表示為:
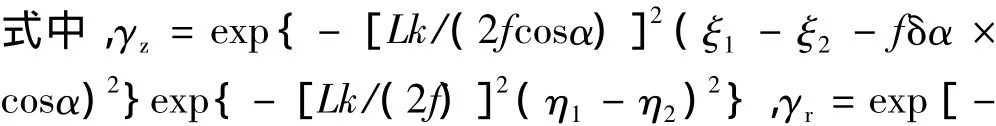
γ = γz·γr(2)其中 γr中含有與表面粗糙度相關的因子。為了得到簡化的相關度,即把相關度簡化成只與表面粗糙度有關的函數,可以令γz=1,即令:ξ1-ξ2-fδαcosα =0,η1- η2=0;此時,相關度 γ 取得最大值,且γ=γr。由(2)式可計算粗糙表面的輪廓均方根偏差:

1.2 角度散斑相關度峰值的計算
定義角度散斑相關度:
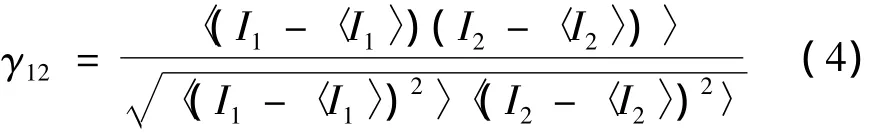
式中,〈…〉表示平均。
當入射角改變δα時,對應的散斑圖像在ξ-η面上沿ξ軸移動了fδαcosα,因此當改變角度照射粗糙表面上同一區域時,所采集的散斑圖像的相關度不等于γr,且所采集的散斑圖像過大,直接計算相關度計算量大,影響測量速度,所以選取散斑圖子區域進行相關度峰值計算。
散斑圖子區域的大小選擇對測量精度有一定影響。如果區域太小,包含的信息量不夠,難以準確匹配兩幅散斑圖的相關區域;如果區域太大則包含太多無用的信息,會降低測量速度。本實驗中,選取像素大小為200×200的散斑子區域作為待處理圖像。
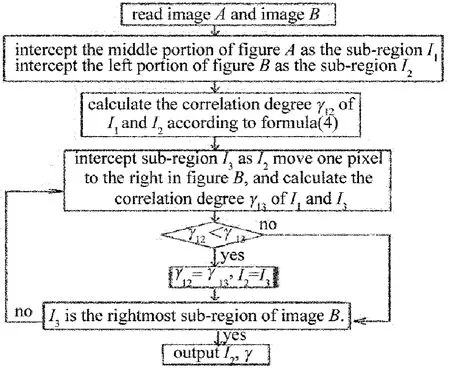
Fig.2 Program flow chart of MATLAB
MATLAB是國際公認的優秀的數值計算軟件,利用MATLAB進行圖像數據的處理,完成相關度峰值的自動獲取,本文中設計的程序流程圖如圖2所示。圖中,記錄角度改變前后的散斑圖分別為圖像A和圖像B,I1,I2和I3為截取的散斑圖子區域。利用循環算法分別截取散斑圖子區域,并計算兩散斑圖子區域的相關度,讀取相關度峰值γ并輸出,再通過(3)式計算即可求得粗糙度σ。
2 表面粗糙度測量裝置與實驗方法
實驗中的關鍵部件是激光器和高分辨率CCD。其中激光器為He-Ne激光器,功率為5mW,波長為632.8nm。CCD為美國的 SI-6600型,面陣尺寸為7.7mm ×10.5mm,像元尺寸為 3.5μm ×3.5μm,分辨率為2048×2950。被測物體為平銑的粗糙度分別為0.8μm,1.6μm,3.2μm 和6.4μm 的標準粗糙度模塊。
圖3為遠場角度散斑強度相關測量表面粗糙度的光路,圖4為其實驗裝置圖。由激光器發出的激光束,經分束器BS、準直擴束系統C形成準直平行光束,照射到待測物體的粗糙表面O,被表面漫反射后,再經過平面反射鏡M1和傅里葉透鏡L1,由 CCD攝像機接收。轉動待測粗糙表面,使入射角發生改變,先后記錄改變前后的散斑圖。用分束器分出一束激光束經反射鏡M2照射到與待測粗糙表面固定在一起的反射鏡M3,再由接收屏S接收,從而形成光指針,以測量平面鏡的轉動角度。將反射鏡與粗糙表面固定在一起除了能起到光指針的作用,代替了精密轉角儀,也能同時保證激光束照射的是粗糙表面的同一位置。
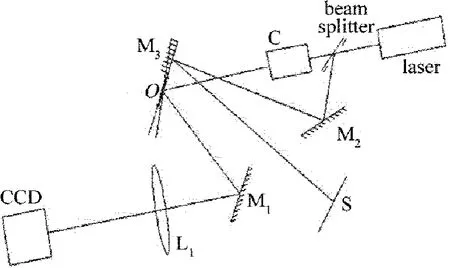
Fig.3 Experimental optical layout of surface roughness measurement using angular-speckle correlation method

Fig.4 Experimental setup and the measured objecta—experimental setup b—the reflective mirror and the measured surface
實驗中首先用CCD記錄下粗糙度模塊初始位置的散斑圖,然后水平轉動待測粗糙表面,記錄下轉動微小角度之后的散斑圖,并記錄激光光斑在接收屏上的移動距離。因為角度的改變,接收散斑圖也會發生δαfcosα的位移,利用反射鏡 M1和傅里葉透鏡L1使CCD能夠完全接收散斑圖像。再利用MATLAB程序尋找僅與表面粗糙度有關的相關度峰值。圖5a和圖5b分別為改變角度前后的散斑圖子區域,圖5c為實驗用的待測粗糙表面。

Fig.5 Standard sample block and speckle patternsa—speckle pattern 1 b—speckle pattern 2 c—standard sample block
3 實驗結果
由遠場角度散斑強度相關理論(3)式可得出粗糙度σ與相關度γ和入射角改變量δα的關系。圖6為入射角α=30°時,粗糙度σ與相關度γ及入射角改變量δα的模擬曲線。
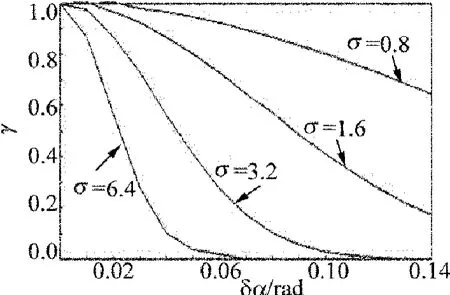
Fig.6 Simulation curves of roughness,correlation degree and incident angles
根據圖6曲線,不同的表面粗糙度在對應不同的角度改變量時會得到不同的相關度,選取適當的角度改變量可得到較好的相關度,有利與進一步得到準確度較高的測量結果。因此在實驗中,選取的角度改變量在0.02rad~0.14rad。
為了驗證方法的可行性,利用圖4裝置分別對標稱值為6.4μm,3.2μm,1.6μm 和0.8μm 的標準粗糙面進行了5次測量。測量結果與標準表面粗糙度標稱值進行比較,如表1所示。
由表1中散斑表面粗糙度測量結果可以看出:在角度改變量增加時,相關度峰值相應降低,與理論曲線相符。所測相關度峰值多數小于理論值,所測粗糙度大于模塊標稱值。測量誤差主要來源實驗光路、入射角和角度改變量的測量誤差。選擇不同的入射角可以測量不同的粗糙度范圍。在選取適當角度變化量的情況下,本系統能得到較好的結果,且對粗糙度較大的粗糙面進行測量時測量誤差較小。
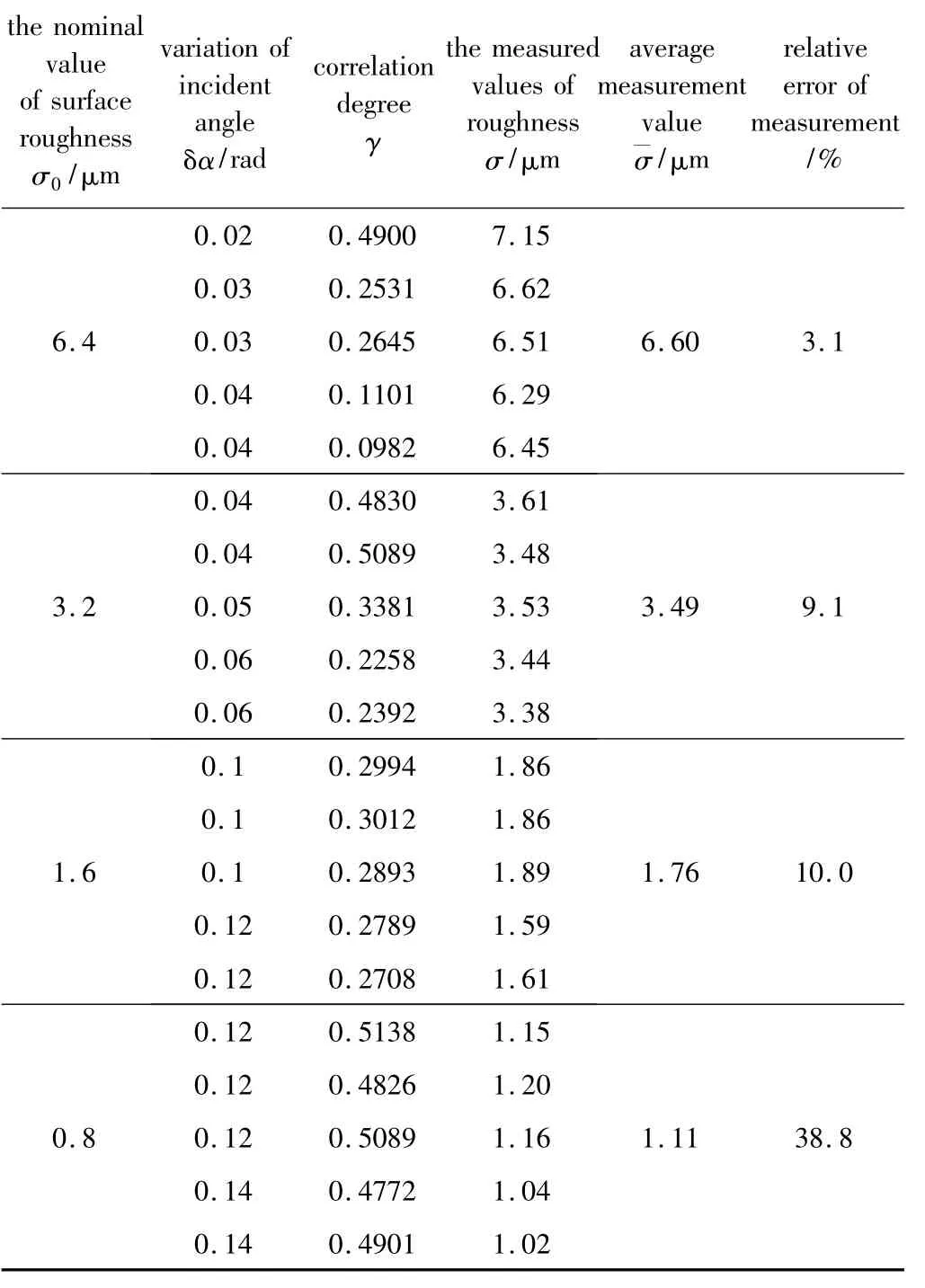
Table 1 Measurement results of surface roughness at incidence angle of 30°
4 結論
基于角度散斑相關原理對平銑表面粗糙度樣塊的粗糙度進行了實驗研究。對各樣塊分別在不同區域、多個不同入射角下采集了遠場散斑圖像。在實驗光路中采用了光指針來精確轉動角度,使在簡單實驗條件下達到相當高的轉動精度,提高了測量準確度。并基于MATLAB軟件編寫的配套程序,在數據處理中實現散斑圖相關度最大值的自動計算,提高了測量速度和自動化程度。當入射中心角為30°左右時,對粗糙度標稱值大于1.6μm物體表面,該方法的測量相對誤差優于10%;表面粗糙度標稱值減小時,測量相對誤差增大。測量表面粗糙度的精度與入射角相關,尋找合適的入射角可提高實驗系統的精度。
[1] ZHOU L L,ZHAO X Z.In-process measurement of surface roughness using laser and other techniques[J].Laser Journal,2004,25(3):4-8(in Chinese).
[2] WANG Zh P,ZHANG X F,ZHANG Y N.Progress on optical measurement of surface roughness[J].Transducer and Microsystem Technologies,2007,26(9):4-6(in Chinese).
[3] BERND R.Application of speckle-correlation methods to surfaceroughness measurement:a theoretical study[J].Journal of the Optical Society of America,1986,3(8):1297-1304.
[4] LIU H B,ZHOU Y J,WANG Ch L.Surface roughness measurement based on dichormatic digital speckle correlation[J].Acta Optica Sinica,2011,31(4):1-7(in Chinese).
[5] ZHANG J W,YUAN Z H,ZHANG Y H.Analysis on large radius of curved surface Roughness trichoromatic laser autocorrelation measurement[J].Laser & Optoelectronics Progress,2011,48(1):41-45(in Chinese).
[6] TOH S L,QUAN C,WOO K C,et al.Whole field surface roughness measurement by laser speckle correlation technique[J].Optics & Laser Technology,2001,33(6):427-434(in Chinese).
[7] WANG J,LIU H B.Numercial simulation of surface-roughness measurement based on angular-speckle correlation method using spatial average[J].Acta Optica Sinica,2007,27(2):260-264(in Chinese).
[8] ULF P.Surface roughness measurement on machined surfaces using angular speckle correlation[J].Journal of Materials Processing Technology,2006,180(1/3):233-238.
[9] YAMAGUCHI I,KOBAYASHI K,YAROSLAVSKY L.Measurement of surface roughness by speckle correlation[J].Optical Engineering,2004,43(11):2753-2761.
[10] LIU H B,LIU Ch L.Experimental research on surface roughness measurement using angular-speckle correlation[J].Acta Optica Sinica,2009,29(3):697-701(in Chinese).
[11] LIU M.Study on the distribution properties of image plane speckle fields produced by Gaussian correlation weak scattering screens[J].Acta Physica Sinica,2013,62(9):094204(in Chinese).
[12] LIANG Zh J,WANG K F,GU G Q,et al.Digital speckle image correlation method base on particle swarm optimization algorithm[J].Laser Technology,2014,38(5):603-607(in Chinese).

