一種改進波形設計的LFMCW雷達多目標檢測方法
陸小凱,劉國華
(中國船舶重工集團公司第723研究所,揚州 225001)
?
一種改進波形設計的LFMCW雷達多目標檢測方法
陸小凱,劉國華
(中國船舶重工集團公司第723研究所,揚州 225001)
針對線性調頻連續波(LFMCW)雷達中存在的距離-速度耦合及多目標頻譜配對問題,提出了一種改進波形設計的方法。該方法通過發射梯形波調制的連續波信號,不僅可以解距離-速度耦合,而且能進行上升段和下降段頻譜配對。仿真結果證實了該方法的有效性。
線性調頻連續波;梯形調制;頻譜配對;多目標檢測
0 引 言
線性調頻連續波(LFMCW)雷達是一種通過發射頻率受線性調制的連續波信號以獲取目標參數信息的雷達體制,它具有分辨率高、無測距盲區、低截獲和結構簡單等一系列優點[1]。近年來,線性調頻連續波技術得到了廣泛的關注和發展。在軍事領域,線性調頻連續波雷達在導彈精密末制導、引信、機載導航設備中的應用越來越廣泛;在民用領域,其在環境遙感、交通管制等應用中也發揮著越來越重要的作用[2-3]。
目前LFMCW雷達發射波形廣泛采用鋸齒波調制和對稱三角波調制方式。鋸齒波調制下的線性調頻連續波雷達存在嚴重的距離-耦合現象[4],而采用對稱三角波調制能夠在一定程度上克服上述問題,但在多目標環境中存在調頻上升段和下降段頻譜配對難的問題。為此,本文提出一種改進波形設計的方法,即采用梯形波調制的連續波作為發射信號。該方法不僅可以解距離-速度耦合,而且可以有效進行頻率上升段和下降段頻譜配對,適用于多目標環境。
1 LFMCW雷達工作原理
典型的LFMCW雷達系統采用三角波調制的發射波形,其在工作過程中,雷達接收機接收回波信號并與發射信號進行混頻得到差頻信號,經模數轉換采樣后作快速傅里葉變換得到頻譜信息。接下來對該頻譜信息分調頻上升段和下降段進行分析處理便可得到目標的參數信息,其工作原理如圖1所示。
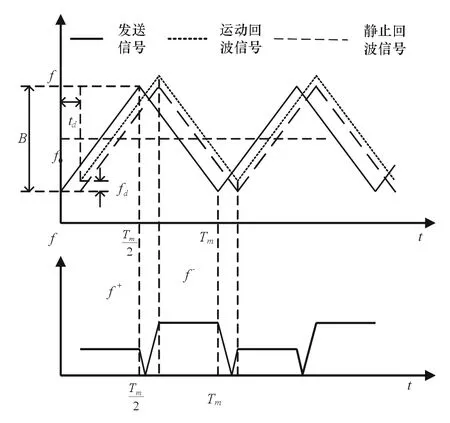
圖1 三角波LFMCW雷達原理圖
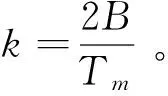
(1)
(2)
由式(2)可推出運動目標的距離和速度,表示為:
(3)
由式(3)可以看出,只要知道目標差頻信號在調頻上升段和下降段的頻譜信息即可算得目標的距離、速度信息。
2 三角波調制下的頻譜配對問題
三角波調制的LFMCW雷達系統工作環境中僅存在單個目標時,不用考慮頻譜配對。而當目標增多時,無法輕易得到各目標譜線的配對關系,進而無法得到目標的參數。若考慮所有情況,n個目標就存在n2組數據。為簡化推導,考慮雷達工作環境中存在3個運動目標的情形。差頻信號通過目標檢測算法后,其在調頻上升段和下降段分別存在3根譜線,分別設為fa1、fa2、fa3和fb1、fb2、fb3。將調頻上升段的3個譜線和下降段的3個譜線兩兩配對,由:
可得到9組距離和速度:
由理論可知上面矩陣中只有對角線的3組是真實目標所對應的參數信息。如果目標數繼續增加,按照此法得到的虛假目標的數量將以n2-n倍的速度遞增,大大增加了數據冗余度,這樣的系統是無法正常工作的。因此,差頻信號在經過頻域檢測后,需要加入頻譜配對算法。
3 改進波形設計方法
現有的頻譜配對方法主要是頻譜特征參數相似法[5]。頻譜特征參數相似法利用譜線的面積、相位、功率等特征參數的相似性來進行頻譜配對,然而在實際應用中該算法十分復雜且無法檢驗配對正確與否,可靠性很低。另外,文獻[6]提出一種采用變周期調頻連續波作為發射波形的方法,可以避開頻譜匹配程序,然而變周期調頻連續波信號在工程上實現的難度很大。
為了在多目標環境中準確識別出真實目標,并保證測距的精度,本文考慮從波形設計的角度切入,提出一種梯形波調制波形設計的方法,波形圖如圖2所示。
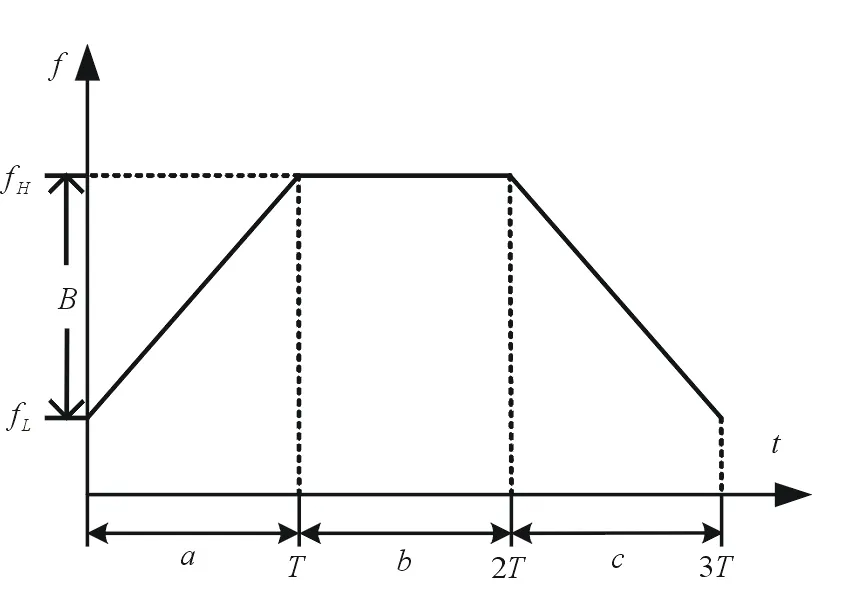
圖2 梯形波LFMCW調制波形
該信號由頻率上升段a、恒頻段b以及頻率下降段c3段信號組成,每段信號的持續時間都為T,調頻帶寬為B。其工作原理如圖3所示。
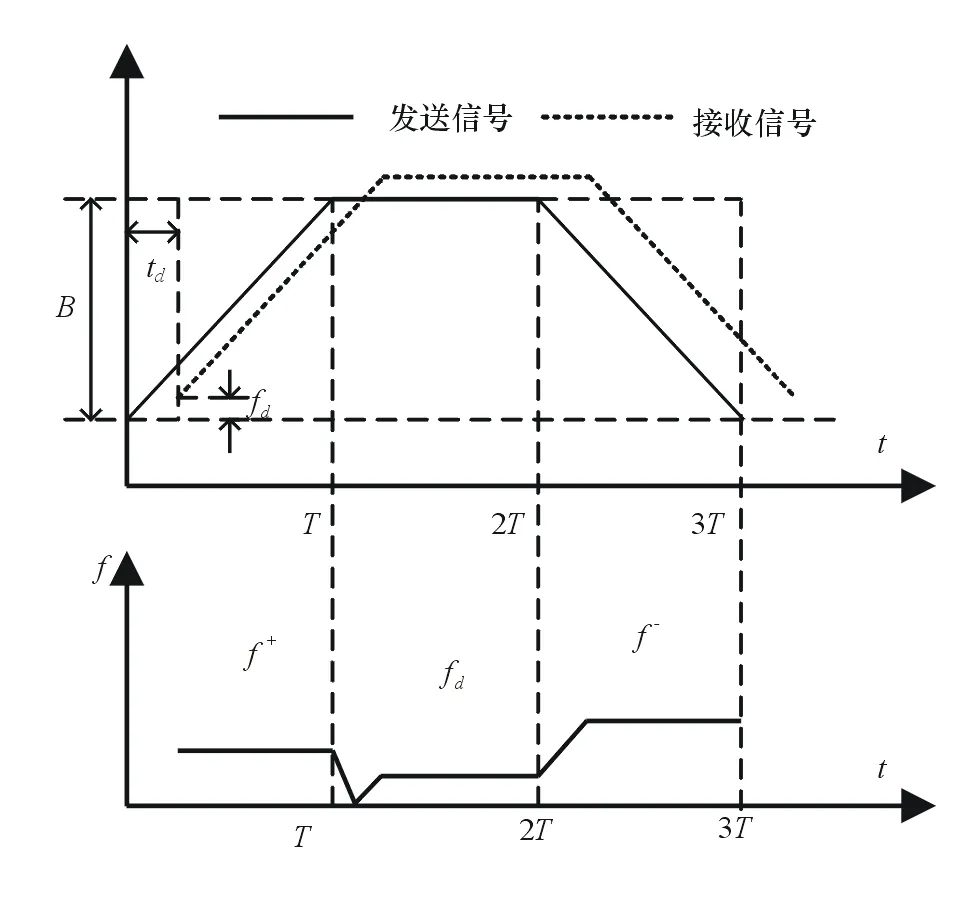
圖3 梯形波LFMCW雷達原理圖
梯形波LFMCW雷達系統的測距測速原理在頻率上升段和下降段時類似于三角調制的情形。為解決頻譜配對的問題,在三角波調制的基礎上增加一個恒定掃頻段,即圖2中T~2T的恒頻段b,該恒頻段產生的差頻信號的頻率即目標的多普勒頻偏fd。在多目標環境中,用fdk表示第k個目標在恒頻段對應差頻信號的譜線。由式(2)可推出:
(4)
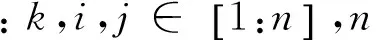
由上式可完成目標k在頻率上升段和下降段對應譜線的配對。
4 計算機仿真分析
4.1 波形參數設計
采用梯形波調制時,利用目標的多普勒頻率fd來確定目標在調頻上升段譜線f+和下降段譜線f-的配對。在慢速目標環境中,fd相對于f+和f-較小,頻率分辨率有限,在恒頻段檢測頻譜時容易丟失部分目標的多普勒頻率信息,從而導致多目標識別的困難。因此,該波形設計更多適用于快速目標的環境。
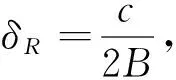
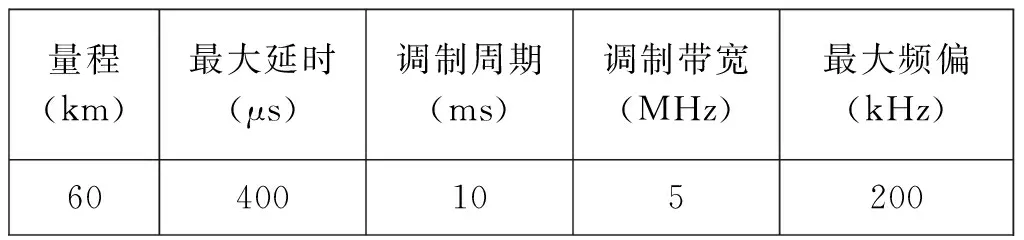
表1 梯形波設計參數
4.2 算法仿真分析
為了驗證本文提出的波形設計方法的有效性,下面利用MATLAB仿真平臺對該方法進行仿真分析。仿真中,雷達工作參數選擇如4.1節,選取4個典型目標,目標參數如表2所示。
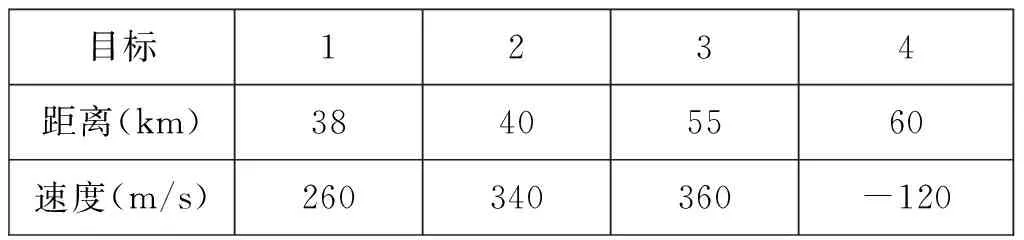
表2 多目標參數
由表2可以看出:目標1和2之間距離相近,但速度不同;目標2和3之間速度相近,但有一定的距離;目標4與其他目標速度相反。假設雷達工作在理想環境,差頻信號在調頻上升段和下降段經快速傅里葉變換(FFT)后的頻譜如圖4所示。
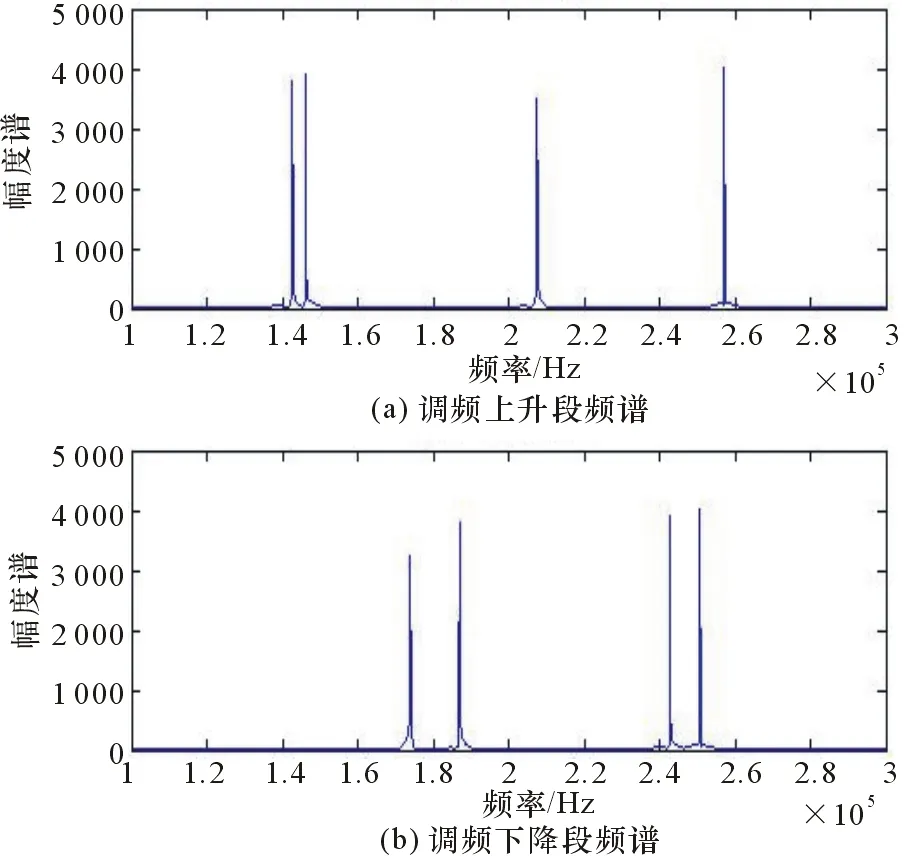
圖4 頻率上升段和下降段頻譜
由圖4可以看出,差頻信號在調頻上升段和下降段分別存在4個譜峰,這正對應著4個目標。依據式(4)將頻率上升段和下降段的4根譜線兩兩配對可得到16個多普勒頻率信息,如圖5所示。
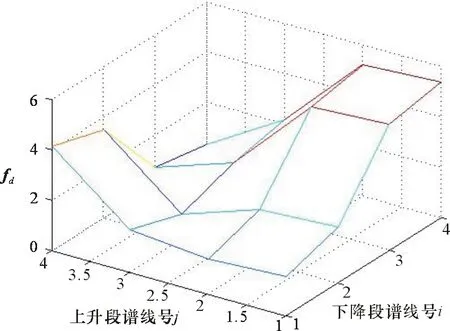
圖5 匹配后的多普勒頻率三維圖
對圖5進行峰值搜索可得到16個多普勒頻率構成的矩陣fd(4×4):
再對恒頻段的差頻信號作快速傅里葉變換(FFT)可得其頻譜如圖6所示。
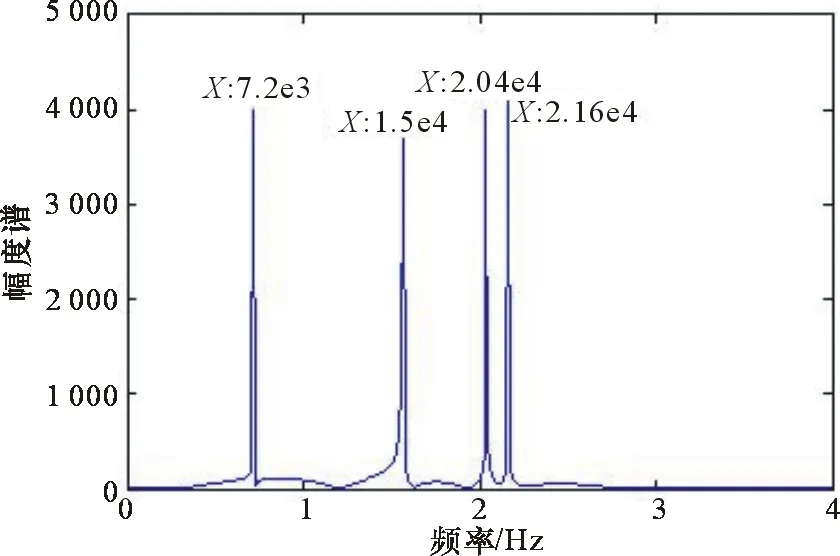
圖6 恒頻段頻譜
依據理論可知,圖6中4根譜線即為4個運動目標對應的多普勒頻率,圖中已標注出它們的頻率值,分別為7.2e3、1.56e4、2.04e4、2.16e4。再將它們與之前計算得到的矩陣fd(4×4)比對可發現,矩陣中(1,1)、(2,2)、(3,4)、(4,3)位置上的值與恒頻段得到的目標多普勒頻率相同,進而可推出調頻上升段中1,2,3,4號譜線與下降段中1,2,4,3號譜線是相互匹配的。
5 結束語
線性調頻連續波雷達多目標檢測問題一直是阻礙其得到廣泛應用的難題之一。本文考慮從波形設計的角度切入,提出一種梯形波調制波形設計的方法。
該方法利用頻率上升段和下降段解距離-速度耦合,利用恒頻段進行目標譜線配對。
仿真結果證實了該方法可在目標譜線正確檢測后有效分辨出不同目標,對工程設計方案有一定的指導意義。
[1] 丁鷺飛,耿富錄.雷達原理[M].第3版.西安:西安電子科技大學出版社,2002.
[2]StoveAG.LinearFMCWradartechnique[J].RadarandSignalProcessing,IEEProceeding-F,1992,139(5):343-350.
[3]VesuovoR.Patternsynthesiswithnullconstraintsforcirculararraysofequallyspacedisotropicelements[J].MicowaveAntennasPropagation,IEEProceedings,1996,143(2):103- 106.
[4] 楊建宇,凌太兵,賀峻.LFMCW雷達運動目標檢測與距離速度去耦合[J].電子與信息學報,2004,26(2):169-173.
[5] 史林,張琳.調頻連續波雷達頻譜配對信號處理方法[J].西安電子科技大學學報(自然科學版),2003,30(4):534-538.
[6] 徐濤,金昶明,孫曉偉,夏冠群.一種采用變周期調頻連續波雷達的多目標識別方法[J].電子學報,2002,30(6):861-863.
A Method of Improving Waveform Design for LFMCW Radar Multi-target Detection
LU Xiao-kai,LIU Guo-hua
(The 723 Institute of CSIC,Yangzhou 225001)
Aiming at the problems of range-velocity coupling and multi-target spectrum matching in linear frequency modulation continuous wave (LFMCW) radar,this paper proposes a method to improve waveform design.By transmitting continuous wave signal modulated by trapezoidal wave,not only the range-velocity coupling can be solved,but also the frequency spectrums of rising segment and falling segment can be matched.Simulation results validate the validity of the method.
linear frequency modulation continuous wave;trapezoidal modulation;spectrum matching;multi-target detection
2014-10-08
TN958
A
CN32-1413(2015)02-0033-04
10.16426/j.cnki.jcdzdk.2015.02.010

