一種基于峭度和記憶梯度的變步長盲均衡算法

郭 強，姜 暉

(電子工程學院，合肥 230037)

?

一種基于峭度和記憶梯度的變步長盲均衡算法

郭 強，姜 暉

(電子工程學院，合肥 230037)

分析了軍事通信中傳統恒模盲均衡算法的基本原理，并針對恒模算法收斂速度慢、易陷入局部極小點、收斂速度與穩態剩余誤差之間矛盾突出的缺點,提出一種基于峭度和記憶梯度的變步長算法。經過理論分析和實驗仿真，證明改進后的算法較傳統算法具有更好的均衡效果。

恒模算法；峭度；記憶梯度

0 引 言

隨著現代戰爭的發展，作戰環境日趨復雜，如何確保復雜電磁信號環境下可靠、穩定、快速的軍事通信是信息作戰的重要內容。然而，由于信號傳輸環境復雜、敵方施加干擾等原因，通信信號在傳輸過程中，常會因為信道畸變而產生碼間干擾(ISI)，這嚴重影響了接收信號的質量，降低了軍事通信的可靠性和穩定性。因此，必須使用可靠的均衡技術對信道引起的畸變進行校正，以消除或減小ISI的影響，提高軍事通信的質量和效率[1]。盲均衡不需要發射端發送訓練序列，可僅利用接收信號對畸變信道進行有效校正，降低傳輸誤碼率，是目前飛速發展的數字通信系統中的關鍵技術之一，在現代軍事通信中有著非常廣泛的應用[2]。

恒模算法是在軍事通信中被廣泛應用的一種盲均衡算法，其存在以下不足：

(1) 對高斯噪聲無免疫性；

(2) 易陷入局部極小點，收斂速度較慢；

(3) 迭代步長恒定，存在收斂速度與穩態誤差之間無法平衡的矛盾。

本文結合傳統的恒模算法(CMA)，提出一種基于峭度和記憶梯度的變步長恒模算法(VS-KMGCMA)。算法將誤差信號的峭度作為代價函數，以實現對高斯噪聲的抑制；將記憶梯度法引入均衡器權值最優化過程中以獲取全局最優點；并用梯度的變化量作為控制步長變化的參數，加快收斂速率并消除固定步長下收斂速度和穩態誤差之間無法平衡的矛盾。

1 傳統恒模算法

CMA算法是Bussgang類盲均衡算法的一個特例，其中心思想是構造一個具有凹凸性質的代價函數，再通過算法調節均衡器的抽頭系數使代價函數取得最大或最小值，以此來達到均衡的目的[3]。Bussgang類盲均衡器的原理如圖1所示。

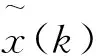
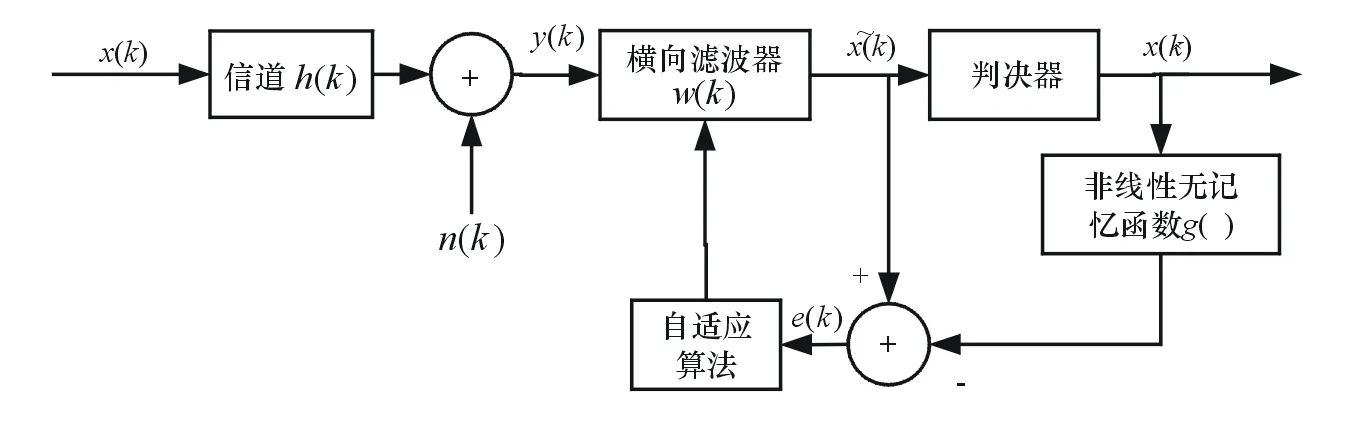
圖1 Bussgang類盲均衡器的原理

由圖1可知均衡器輸出信號為：

(1)

式中：W(k)為均衡器抽頭系數向量；w(k)為均衡器抽頭系數；N為輸入數據總量。

誤差函數為：

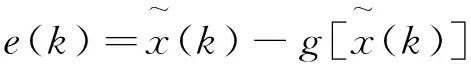
(2)

在CMA算法中定義為：

(3)

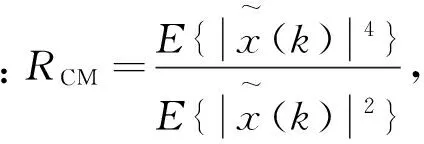
CMA算法的代價函數J(k)為:

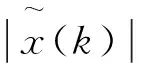
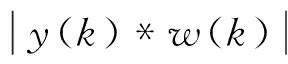
(4)

算法的目標為代價函數J(k)的最小化，而由公式(4)可知，J(k)的取值取決于y(k)和w(k)，可將算法的目標看作是多維非凸曲面中求解最小值的問題，這是一個無約束最優化問題。

均衡器抽頭系數的迭代公式為：

W(k)+2·μ·e(k)·YH(k)

(5)

式中：μ為迭代步長因子，通常取足夠小的恒定值。

將式(3)代入式(5)得：

(6)

2 基于峭度和記憶梯度的變步長盲均衡算法(VS-KMGCMA)

2.1 峭度(Kurtosis)的引入

信號的峭度即信號零時延的四階累積量，根據信號的高階累積量可以抑制高斯噪聲的特性，可以將峭度引入到CMA算法中，用誤差信號的峭度構造盲均衡抽頭權值最優化的代價函數，提高算法處理復雜噪聲的能力[4]。

根據定義，誤差信號的峭度為：

其具有如下性質：

性質1：若e1(k)與e2(k)是統計獨立的隨機過程，則二者和的峭度為二者峭度之和，即：

K[e1(k)+e2(k)]=K[e1(k)]+K[e2(k)]

(8)

性質2：若e(k)為零均值的高斯過程，則其峭度為0，即：

K[e(k)]=0

(9)

性質3：若e1(k)為非高斯隨機過程，e2(k)為高斯隨機過程，則由前面兩式可知：

K[e1(k)+e2(k)]=K[e1(k)]+K[e2(k)]=K[e1(k)]

(10)

由上式可知，誤差信號的峭度具有完全抑制高斯噪聲的能力。

利用峭度的這種特性，定義均衡器抽頭權值最優化的代價函數為：

J(k)=-K[e(k)]=3·E2[e2(k)]-E[e4(k)]

(11)

由以上分析可知，峭度的引入可以提高CMA算法對高斯噪聲的抑制能力，改善均衡性能，更方便實現信號的實時恢復。

2.2 記憶梯度法(MGM)

由式(5)可知，在均衡器抽頭系數的迭代過程中，CMA算法采用的是最快梯度下降法，該方法的優點是計算量較小、結構簡單，但很容易導致代價函數曲面進入平坦區域而大幅增加迭代次數，降低收斂速度；另外，由于代價函數曲面中存在多個極小點且多為局部極小，算法極易陷入局部極小點而無法自拔，無法獲得全局最優。

一般情況下，共軛梯度算法是求解大型無約束優化問題的有效算法，作為一種改進型的最速梯度下降算法，它在記憶前面迭代信息的基礎上進行下一次迭代，具體運用于恒模算法中，其迭代方程為：

W(k+1)=W(k)+μ·D(k)

(12)

(13)

(14)

當參數β(k)取不同的公式時就取得不同的共軛梯度算法。共軛梯度算法增加了對之前梯度信息的利用，避免了對矩陣的計算和存儲，相比于快速梯度下降法，該類算法更加可靠、高效，更易得到快速、穩定且可全局收斂的算法。20世紀60年代，Miele[5]等人提出了記憶梯度算法，作為共軛梯度算法的一種推廣，該類算法在迭代過程中無需計算和存儲數據，而且能更加充分地利用之前的迭代信息，還增加了參量的選擇范圍。相比于共軛梯度法，記憶梯度法更利于全局尋優并構造穩定、快速的收斂算法。

W(k+1)=W(k)+μ·D(k)

(15)

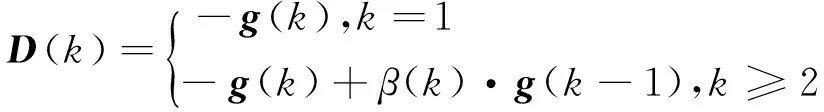
(16)

(17)

ρ為控制參數，可用來控制β(k)的取值范圍。由以上分析可知，相比共軛梯度法，記憶梯度法利用之前梯度信息的程度更大，并且可以通過參數ρ的取值控制記憶信息的取值比例，參數選擇自由度更大，增強了算法的可控性、穩定性[6]。

2.3 變步長思想

在算法收斂初期，均衡關心的問題是算法能否收斂，因此希望使用大步長促使算法盡快收斂；而隨著算法的逐步收斂，均衡期望獲得更好的收斂性能，因此希望步長減小以降低穩態剩余誤差，提高收斂精度[7]。

傳統CMA算法中，步長因子為恒定值，無法跟隨迭代過程而改變大小。這一原因導致算法中存在收斂速度和穩態剩余誤差之間無法平衡的矛盾。而變步長的思想因為簡單、有效而被廣泛應用于解決此矛盾。

在記憶梯度法中，隨著算法的逐步收斂，記憶梯度的改變幅度會逐漸減小并趨于穩定，記憶梯度的變化量為一個單調下降的過程，符合盲均衡中代價函數的期望過程，根據這一特性，可以改步長由恒定值為被梯度信息變化量控制的變量，其迭代公式為：

μ(k+1)=B(k)·μ(k)

(18)

(19)

式中：B(k)為梯度信息變化量；λ為參數，用來控制B(k)的取值范圍，通過改變λ的取值來改善B(k)的大小。

通過梯度信息變化量對步長因子的控制可以保證在迭代初期步長較大，算法盡快地進入收斂狀態；而在算法逐步收斂過程中，B(k)逐漸減小，步長也變小，有利于降低穩態誤差，提高收斂精度。

根據以上分析可知，變步長思想的引入有效解決了傳統恒模算法中收斂速度和穩態剩余誤差之間的矛盾，保證在不增加穩態誤差的前提下提高算法的收斂速度，提升均衡效果。

綜上所述，峭度、記憶梯度法和變步長的引入可以有效提高算法處理復雜噪聲的能力，更易于獲得全局最優解并且加快均衡算法收斂，可以提高算法的可靠性、穩定性和快速性。

公式(11)、(15)、(18)為基于峭度和記憶梯度的變步長盲均衡算法的數學表示。

3 實驗仿真

3.1 仿真條件

為了驗證改進算法在軍事通信盲均衡中的性能，對改進的VS-KMGCMA算法、KMGCMA算法和傳統CMA算法的收斂速度、碼間干擾進行了仿真分析。

在仿真實驗中，設置的均衡器、傳輸信道模型和發射信號的參數如下：均衡器抽頭數為11，采用中心化初始策略，即中心抽頭系數初始值為1，其它抽頭系數初始值取0；步長初始值μ=0.001；信噪比為20dB；傳輸信道為離散數字信道，其沖擊響應函數為h=[0.05,-0.063,0.088,-0.126,-0.25,0.904 7,0.25,0,0.126,0.038,0.088][8]。

發送信號的調制樣式為四進制正交調幅(4QAM)，發送符號數為20 000；用400次蒙特卡洛仿真的統計平均值來評價幾種算法。均衡算法的性能通過剩余碼間干擾的大小來評定，其定義為：

(20)

3.2 仿真結果分析

圖2給出了在信噪比為20dB時，3種算法的均衡性能曲線。由圖2可知:

(1)CMA算法的收斂速度最慢，碼間干擾最嚴重，均衡效果在3種算法中最差；

(2) 引入峭度和記憶梯度法后的KMG-CMA算法和VS-KMGCMA算法在剩余碼間干擾、收斂速度方面的性能都有了大幅提升；

(3)VS-KMGCMA算法由于引入變步長的思想，比KMGCMA算法的收斂速度更快，在經過大約7 000次迭代后便可收斂至-33dB，而KMGCMA則要經過大概14 000次迭代后才可達到相同的收斂狀態。

由此可見，變步長思想的引入極大提高了算法的收斂速度，解決了穩態誤差和收斂速度之間的矛盾。

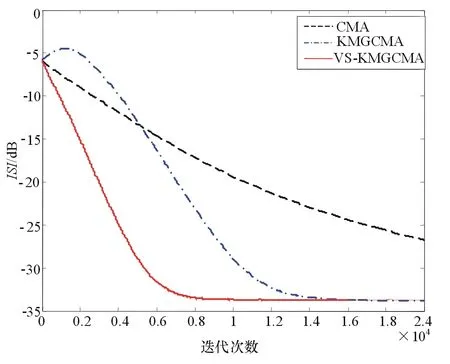
圖2 剩余碼間干擾收斂曲線

圖3、圖4為信號經過信道h前后的星座圖，可以明顯看出信源信號在經過離散無線信道后發生了明顯的碼間干擾，導致星座圖非常分散，造成信號難以辨認，影響信號的檢測。

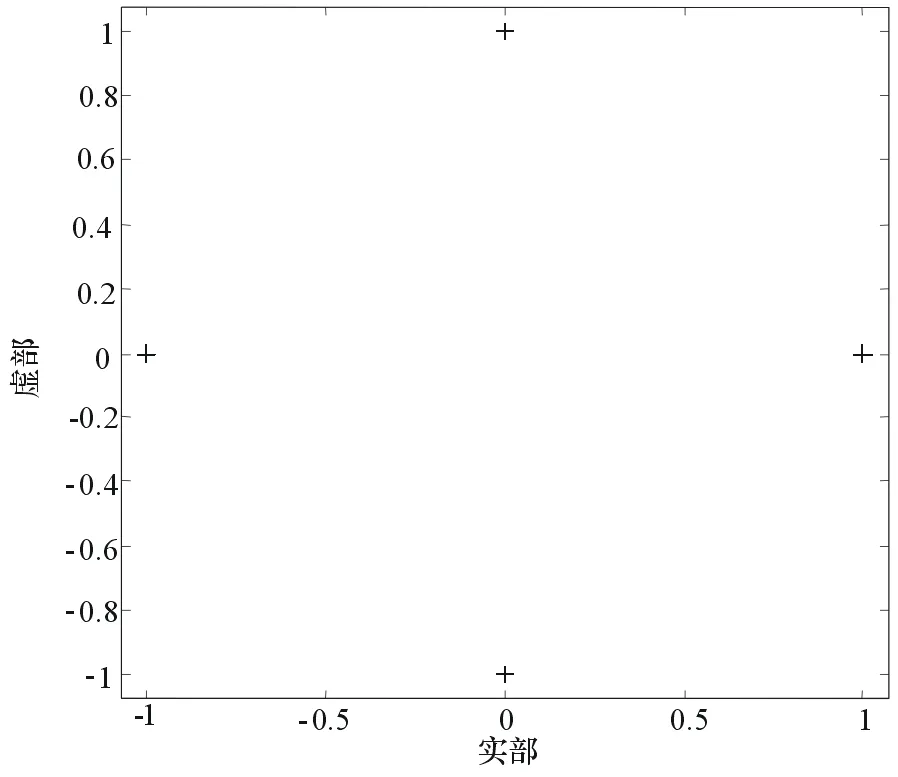
圖3 發送信號星座圖

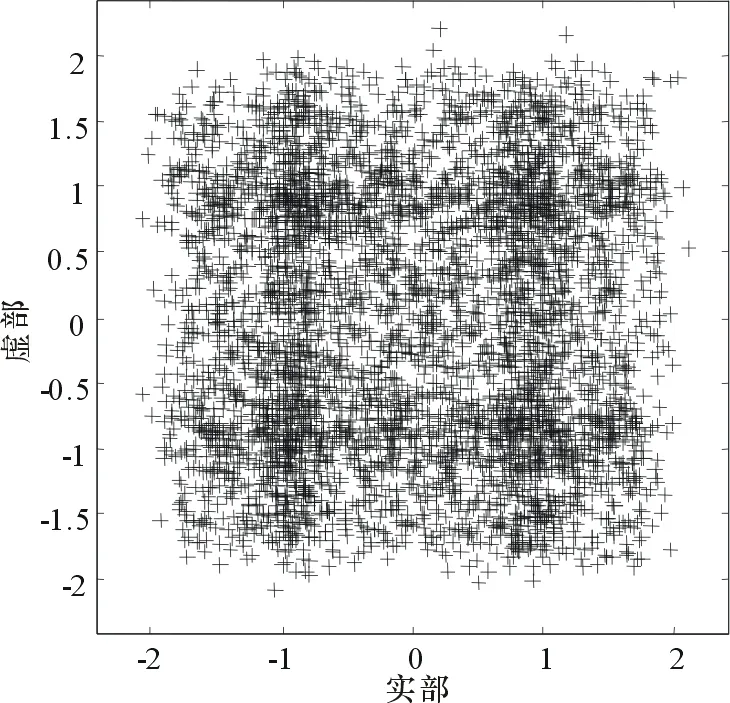
圖4 均衡輸入信號星座圖

圖5、圖6、圖7為信號經過3種算法均衡后的輸出星座圖。由于VS-KMGCMA算法引入了峭度、記憶梯度法和變步長的思想，不僅提高了對高斯噪聲的免疫能力，更易獲得全局最優點，而且解決了固定步長下穩態誤差和收斂速度之間的矛盾，所以該算法可以獲得最好的收斂性能。因此，其均衡輸出的星座點清晰緊湊，更好地收斂至信源點附近，即穩態誤差和碼間干擾更小，均衡性能更加優越。

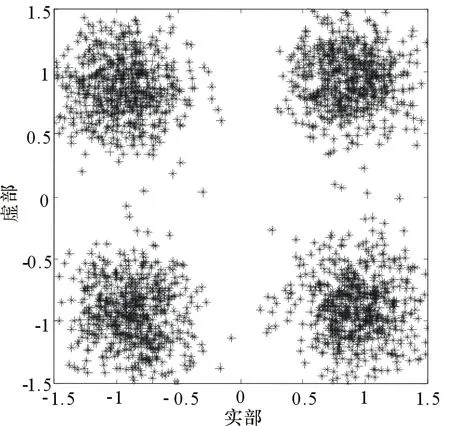
圖5 CMA均衡后信號星座圖

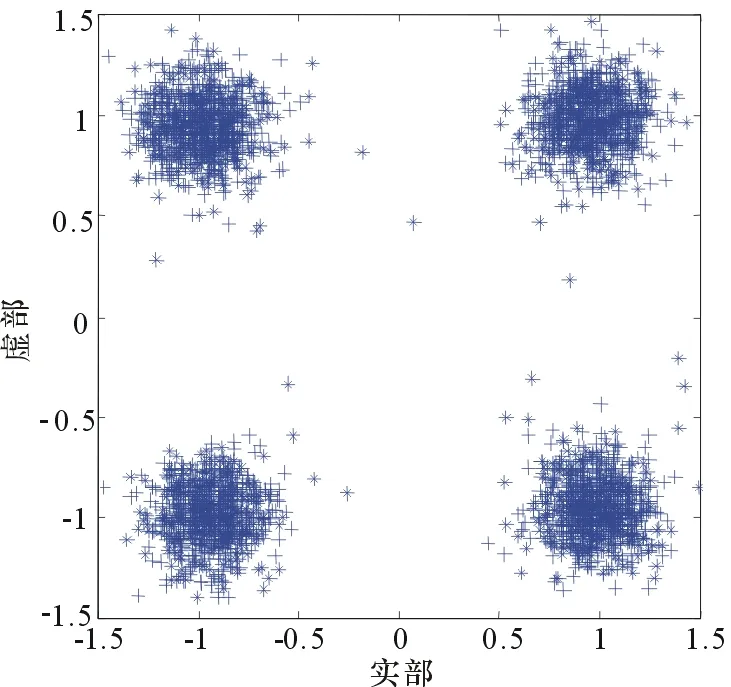
圖6 KMGCMA均衡后信號星座圖

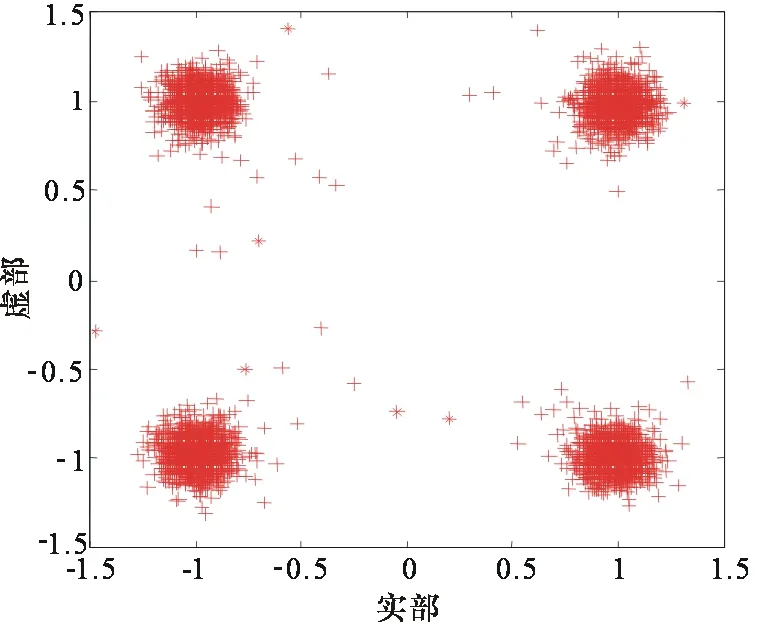
圖7 VS-KMGCMA均衡后信號星座圖

以上仿真實驗可以說明，改進后的算法相比于傳統恒模算法，收斂速度加快，性能更好，更有利于獲得好的均衡效果。

4 結束語

本文提出的改進算法將誤差信號的峭度作為代價函數，并將記憶梯度法引入到均衡器抽頭系數的迭代過程中，同時將梯度的變化量作為控制步長的參量。理論分析表明，新算法可以有效加快收斂速度，提高均衡性能。實驗仿真結果也證明：該算法在收斂后的碼間干擾、均方誤差、收斂速度等方面的性能均優于傳統恒模算法。

[1] 華亞維.短波數據傳輸自適應均衡技術研究與實現[D].西安:西安電子科技大學，2009.

[2] 楊賓，王大磊，吳瑛，王秀秀.利用無約束函數的QAM 信號自適應盲均衡方法[J].信號處理,2014,30(4):399-404.

[3] 張丹丹.盲均衡算法及其FPGA實現的研究[D].秦皇島:燕山大學，2013.

[4] Tanrikulu O,Constantinides A G.Least mean kurtosis:a novel higher-order statistics based adaptive filtering algorithm[J].Electronic Letters,1994,30(3):189- 190.

[5] Miele A,Cantrell J W.Study on a memory gradient method for the minimization of functions[J].Journal of Optimization,Theory and Applications,1969,3(6):459- 470.

[6] 湯京永,葉貞軍.一類全局收斂的記憶梯度算法及其線性收斂性[J].數學進展,2007,36(1):67-75.

[7] 鐘華,金國平，鄭林華.一種新的修正步長盲均衡算法[J].系統仿真學報,2009,21(24):7773-7777.

[8] 趙雅興,劉棟,張寧.一種適用于FPGA實現的盲均衡算法[J].通信學報,2001,22(8):108-111.

A Blind Equalization Algorithm with Variable Step-size Based on Kurtosis and Memory Gradient

GUO Qiang,JIANG Hui

(Electronic Engineering Institute,Hefei 230037,China)

This paper analyzes the basic principle of traditional constant modulus blind equalization algorithm in military communication,and for the disadvantages of the algorithm such as slow convergence speed,being easy to fall into local minimum point and difficult to balance between convergence speed and residual error of steady state,this paper puts forward an algorithm with variable step-size based on kurtosis and memory gradient.Through theoretical analysis and experimental simulation,the improved algorithm is proved to be more effective compared with traditional algorithm.

constant modulus algorithm;kurtosis;memory gradient

2014-10-27

TN911

A

CN32-1413(2015)02-0076-05

10.16426/j.cnki.jcdzdk.2015.02.020